최소 스패닝 트리에 대한 역삭제 알고리즘

GfG Practice에서 사용해 보세요. 최소 스패닝 트리에 대한 역삭제 알고리즘

#practiceLinkDiv { 표시: 없음 !중요; }

역방향 삭제 알고리즘은 다음과 밀접한 관련이 있습니다. 크루스칼의 알고리즘 . Kruskal의 알고리즘에서 우리가 하는 일은 다음과 같습니다: 가중치의 순서를 높여 가장자리를 정렬합니다. 정렬 후 우리는 오름차순으로 가장자리를 하나씩 선택합니다. V = 정점 수인 스패닝 트리에 V-1 가장자리가 있을 때까지 어떤 사이클도 형성하지 않는 스패닝 트리에 이를 포함하면 현재 선택한 가장자리를 포함합니다.

역방향 삭제 알고리즘에서는 모든 가장자리를 정렬합니다. 감소하는 무게의 순서. 정렬한 후 내림차순으로 가장자리를 하나씩 선택합니다. 우리 현재 가장자리를 제외하면 현재 그래프에서 연결이 끊어지는 경우 현재 선택한 가장자리를 포함합니다. . 주요 아이디어는 삭제로 인해 그래프 연결이 끊어지지 않으면 가장자리를 삭제하는 것입니다.

알고리즘:

간선 가중치가 증가하지 않는 순서로 그래프의 모든 간선을 정렬합니다.

MST를 원본 그래프로 초기화하고 3단계를 사용하여 추가 간선을 제거합니다.

나머지 모서리에서 가중치가 가장 높은 모서리를 선택하고 에지를 삭제하면 그래프 연결이 끊어지는지 확인하세요. .
연결이 끊어지면 가장자리를 삭제하지 않습니다.
그렇지 않으면 가장자리를 삭제하고 계속합니다.

삽화:

다음 예를 통해 이해해 보겠습니다.

역삭제2

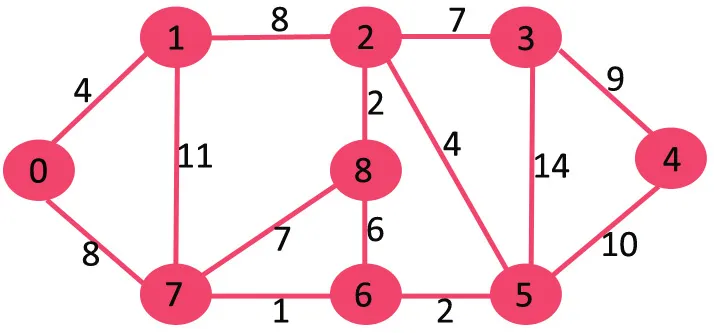
가중치 14의 가장 높은 가중치 가장자리를 삭제해도 그래프가 연결 해제되지 않으므로 제거합니다.

역삭제3

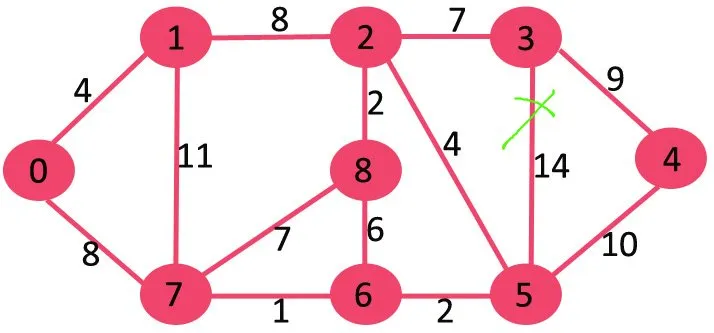
다음으로 11을 삭제하면 그래프 연결이 끊어지지 않으므로 삭제합니다.

역삭제4

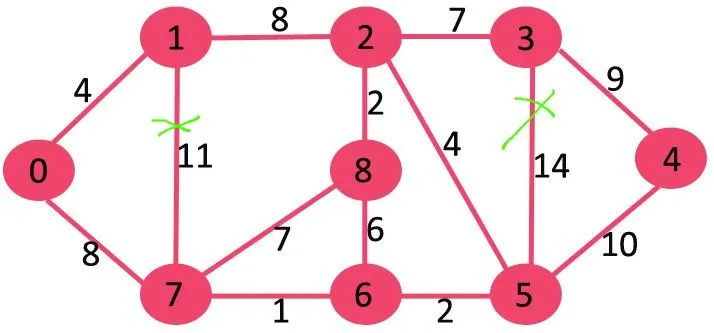
다음으로 10을 삭제하면 그래프 연결이 끊어지지 않으므로 삭제합니다.

역삭제5

다음은 9입니다. 9를 삭제하면 연결이 끊어지므로 삭제할 수 없습니다.

우리는 이 방법을 계속하고 다음 가장자리는 최종 MST에 남아 있습니다.

 Edges in MST   
 (3 4)    
 (0 7)    
 (2 3)    
 (2 5)    
 (0 1)    
 (5 6)    
 (2 8)    
 (6 7)    
     메모 :    동일한 가중치 모서리의 경우 동일한 가중치 모서리의 모서리를 선택할 수 있습니다.  
권장 실습 최소 스패닝 트리에 대한 역삭제 알고리즘    시도해 보세요!       구현:    
 C++      // C++ program to find Minimum Spanning Tree   // of a graph using Reverse Delete Algorithm   #include       using     namespace     std  ;   // Creating shortcut for an integer pair   typedef     pair   <  int       int  >     iPair  ;   // Graph class represents a directed graph   // using adjacency list representation   class     Graph   {      int     V  ;     // No. of vertices      list   <  int  >     *  adj  ;      vector   <     pair   <  int       iPair  >     >     edges  ;      void     DFS  (  int     v       bool     visited  []);   public  :      Graph  (  int     V  );     // Constructor      // function to add an edge to graph      void     addEdge  (  int     u       int     v       int     w  );      // Returns true if graph is connected      bool     isConnected  ();      void     reverseDeleteMST  ();   };   Graph  ::  Graph  (  int     V  )   {      this  ->  V     =     V  ;      adj     =     new     list   <  int  >  [  V  ];   }   void     Graph  ::  addEdge  (  int     u       int     v       int     w  )   {      adj  [  u  ].  push_back  (  v  );     // Add w to v’s list.      adj  [  v  ].  push_back  (  u  );     // Add w to v’s list.      edges  .  push_back  ({  w       {  u       v  }});   }   void     Graph  ::  DFS  (  int     v       bool     visited  [])   {      // Mark the current node as visited and print it      visited  [  v  ]     =     true  ;      // Recur for all the vertices adjacent to      // this vertex      list   <  int  >::  iterator     i  ;      for     (  i     =     adj  [  v  ].  begin  ();     i     !=     adj  [  v  ].  end  ();     ++  i  )      if     (  !  visited  [  *  i  ])      DFS  (  *  i       visited  );   }   // Returns true if given graph is connected else false   bool     Graph  ::  isConnected  ()   {      bool     visited  [  V  ];      memset  (  visited       false       sizeof  (  visited  ));      // Find all reachable vertices from first vertex      DFS  (  0       visited  );      // If set of reachable vertices includes all      // return true.      for     (  int     i  =  1  ;     i   <  V  ;     i  ++  )      if     (  visited  [  i  ]     ==     false  )      return     false  ;      return     true  ;   }   // This function assumes that edge (u v)   // exists in graph or not   void     Graph  ::  reverseDeleteMST  ()   {      // Sort edges in increasing order on basis of cost      sort  (  edges  .  begin  ()     edges  .  end  ());      int     mst_wt     =     0  ;     // Initialize weight of MST      cout      < <     'Edges in MST  n  '  ;      // Iterate through all sorted edges in      // decreasing order of weights      for     (  int     i  =  edges  .  size  ()  -1  ;     i  >=  0  ;     i  --  )      {      int     u     =     edges  [  i  ].  second  .  first  ;      int     v     =     edges  [  i  ].  second  .  second  ;      // Remove edge from undirected graph      adj  [  u  ].  remove  (  v  );      adj  [  v  ].  remove  (  u  );      // Adding the edge back if removing it      // causes disconnection. In this case this       // edge becomes part of MST.      if     (  isConnected  ()     ==     false  )      {      adj  [  u  ].  push_back  (  v  );      adj  [  v  ].  push_back  (  u  );      // This edge is part of MST      cout      < <     '('      < <     u      < <     ' '      < <     v      < <     ')   n  '  ;      mst_wt     +=     edges  [  i  ].  first  ;      }      }      cout      < <     'Total weight of MST is '      < <     mst_wt  ;   }   // Driver code   int     main  ()   {      // create the graph given in above figure      int     V     =     9  ;      Graph     g  (  V  );      // making above shown graph      g  .  addEdge  (  0       1       4  );      g  .  addEdge  (  0       7       8  );      g  .  addEdge  (  1       2       8  );      g  .  addEdge  (  1       7       11  );      g  .  addEdge  (  2       3       7  );      g  .  addEdge  (  2       8       2  );      g  .  addEdge  (  2       5       4  );      g  .  addEdge  (  3       4       9  );      g  .  addEdge  (  3       5       14  );      g  .  addEdge  (  4       5       10  );      g  .  addEdge  (  5       6       2  );      g  .  addEdge  (  6       7       1  );      g  .  addEdge  (  6       8       6  );      g  .  addEdge  (  7       8       7  );      g  .  reverseDeleteMST  ();      return     0  ;   }   
  Java      // Java program to find Minimum Spanning Tree   // of a graph using Reverse Delete Algorithm   import     java.util.*  ;   // class to represent an edge   class   Edge     implements     Comparable   <  Edge  >     {      int     u       v       w  ;      Edge  (  int     u       int     v       int     w  )      {      this  .  u     =     u  ;      this  .  w     =     w  ;      this  .  v     =     v  ;      }      public     int     compareTo  (  Edge     other  )      {      return     (  this  .  w     -     other  .  w  );      }   }   // Class to represent a graph using adjacency list   // representation   public     class   GFG     {      private     int     V  ;     // No. of vertices      private     List   <  Integer  >[]     adj  ;      private     List   <  Edge  >     edges  ;      @SuppressWarnings  ({     'unchecked'       'deprecated'     })      public     GFG  (  int     v  )     // Constructor      {      V     =     v  ;      adj     =     new     ArrayList  [  v  ]  ;      for     (  int     i     =     0  ;     i      <     v  ;     i  ++  )      adj  [  i  ]     =     new     ArrayList   <  Integer  >  ();      edges     =     new     ArrayList   <  Edge  >  ();      }      // function to Add an edge      public     void     AddEdge  (  int     u       int     v       int     w  )      {      adj  [  u  ]  .  add  (  v  );     // Add w to v’s list.      adj  [  v  ]  .  add  (  u  );     // Add w to v’s list.      edges  .  add  (  new     Edge  (  u       v       w  ));      }      // function to perform dfs      private     void     DFS  (  int     v       boolean  []     visited  )      {      // Mark the current node as visited and print it      visited  [  v  ]     =     true  ;      // Recur for all the vertices adjacent to      // this vertex      for     (  int     i     :     adj  [  v  ]  )     {      if     (  !  visited  [  i  ]  )      DFS  (  i       visited  );      }      }      // Returns true if given graph is connected else false      private     boolean     IsConnected  ()      {      boolean  []     visited     =     new     boolean  [  V  ]  ;      // Find all reachable vertices from first vertex      DFS  (  0       visited  );      // If set of reachable vertices includes all      // return true.      for     (  int     i     =     1  ;     i      <     V  ;     i  ++  )     {      if     (  visited  [  i  ]     ==     false  )      return     false  ;      }      return     true  ;      }      // This function assumes that edge (u v)      // exists in graph or not      public     void     ReverseDeleteMST  ()      {      // Sort edges in increasing order on basis of cost      Collections  .  sort  (  edges  );      int     mst_wt     =     0  ;     // Initialize weight of MST      System  .  out  .  println  (  'Edges in MST'  );      // Iterate through all sorted edges in      // decreasing order of weights      for     (  int     i     =     edges  .  size  ()     -     1  ;     i     >=     0  ;     i  --  )     {      int     u     =     edges  .  get  (  i  ).  u  ;      int     v     =     edges  .  get  (  i  ).  v  ;      // Remove edge from undirected graph      adj  [  u  ]  .  remove  (  adj  [  u  ]  .  indexOf  (  v  ));      adj  [  v  ]  .  remove  (  adj  [  v  ]  .  indexOf  (  u  ));      // Adding the edge back if removing it      // causes disconnection. In this case this      // edge becomes part of MST.      if     (  IsConnected  ()     ==     false  )     {      adj  [  u  ]  .  add  (  v  );      adj  [  v  ]  .  add  (  u  );      // This edge is part of MST      System  .  out  .  println  (  '('     +     u     +     ' '     +     v      +     ')'  );      mst_wt     +=     edges  .  get  (  i  ).  w  ;      }      }      System  .  out  .  println  (  'Total weight of MST is '      +     mst_wt  );      }      // Driver code      public     static     void     main  (  String  []     args  )      {      // create the graph given in above figure      int     V     =     9  ;      GFG     g     =     new     GFG  (  V  );      // making above shown graph      g  .  AddEdge  (  0       1       4  );      g  .  AddEdge  (  0       7       8  );      g  .  AddEdge  (  1       2       8  );      g  .  AddEdge  (  1       7       11  );      g  .  AddEdge  (  2       3       7  );      g  .  AddEdge  (  2       8       2  );      g  .  AddEdge  (  2       5       4  );      g  .  AddEdge  (  3       4       9  );      g  .  AddEdge  (  3       5       14  );      g  .  AddEdge  (  4       5       10  );      g  .  AddEdge  (  5       6       2  );      g  .  AddEdge  (  6       7       1  );      g  .  AddEdge  (  6       8       6  );      g  .  AddEdge  (  7       8       7  );      g  .  ReverseDeleteMST  ();      }   }   // This code is contributed by Prithi_Dey   
  Python3      # Python3 program to find Minimum Spanning Tree   # of a graph using Reverse Delete Algorithm   # Graph class represents a directed graph   # using adjacency list representation   class   Graph  :   def   __init__  (  self     v  ):   # No. of vertices   self  .  v   =   v   self  .  adj   =   [  0  ]   *   v   self  .  edges   =   []   for   i   in   range  (  v  ):   self  .  adj  [  i  ]   =   []   # function to add an edge to graph   def   addEdge  (  self     u  :   int     v  :   int     w  :   int  ):   self  .  adj  [  u  ]  .  append  (  v  )   # Add w to v’s list.   self  .  adj  [  v  ]  .  append  (  u  )   # Add w to v’s list.   self  .  edges  .  append  ((  w     (  u     v  )))   def   dfs  (  self     v  :   int     visited  :   list  ):   # Mark the current node as visited and print it   visited  [  v  ]   =   True   # Recur for all the vertices adjacent to   # this vertex   for   i   in   self  .  adj  [  v  ]:   if   not   visited  [  i  ]:   self  .  dfs  (  i     visited  )   # Returns true if graph is connected   # Returns true if given graph is connected else false   def   connected  (  self  ):   visited   =   [  False  ]   *   self  .  v   # Find all reachable vertices from first vertex   self  .  dfs  (  0     visited  )   # If set of reachable vertices includes all   # return true.   for   i   in   range  (  1     self  .  v  ):   if   not   visited  [  i  ]:   return   False   return   True   # This function assumes that edge (u v)   # exists in graph or not   def   reverseDeleteMST  (  self  ):   # Sort edges in increasing order on basis of cost   self  .  edges  .  sort  (  key   =   lambda   a  :   a  [  0  ])   mst_wt   =   0   # Initialize weight of MST   print  (  'Edges in MST'  )   # Iterate through all sorted edges in   # decreasing order of weights   for   i   in   range  (  len  (  self  .  edges  )   -   1     -  1     -  1  ):   u   =   self  .  edges  [  i  ][  1  ][  0  ]   v   =   self  .  edges  [  i  ][  1  ][  1  ]   # Remove edge from undirected graph   self  .  adj  [  u  ]  .  remove  (  v  )   self  .  adj  [  v  ]  .  remove  (  u  )   # Adding the edge back if removing it   # causes disconnection. In this case this   # edge becomes part of MST.   if   self  .  connected  ()   ==   False  :   self  .  adj  [  u  ]  .  append  (  v  )   self  .  adj  [  v  ]  .  append  (  u  )   # This edge is part of MST   print  (  '(   %d     %d   )'   %   (  u     v  ))   mst_wt   +=   self  .  edges  [  i  ][  0  ]   print  (  'Total weight of MST is'     mst_wt  )   # Driver Code   if   __name__   ==   '__main__'  :   # create the graph given in above figure   V   =   9   g   =   Graph  (  V  )   # making above shown graph   g  .  addEdge  (  0     1     4  )   g  .  addEdge  (  0     7     8  )   g  .  addEdge  (  1     2     8  )   g  .  addEdge  (  1     7     11  )   g  .  addEdge  (  2     3     7  )   g  .  addEdge  (  2     8     2  )   g  .  addEdge  (  2     5     4  )   g  .  addEdge  (  3     4     9  )   g  .  addEdge  (  3     5     14  )   g  .  addEdge  (  4     5     10  )   g  .  addEdge  (  5     6     2  )   g  .  addEdge  (  6     7     1  )   g  .  addEdge  (  6     8     6  )   g  .  addEdge  (  7     8     7  )   g  .  reverseDeleteMST  ()   # This code is contributed by   # sanjeev2552   
  C#      // C# program to find Minimum Spanning Tree   // of a graph using Reverse Delete Algorithm   using     System  ;   using     System.Collections.Generic  ;   // class to represent an edge   public     class     Edge     :     IComparable   <  Edge  >     {      public     int     u       v       w  ;      public     Edge  (  int     u       int     v       int     w  )      {      this  .  u     =     u  ;      this  .  v     =     v  ;      this  .  w     =     w  ;      }      public     int     CompareTo  (  Edge     other  )      {      return     this  .  w  .  CompareTo  (  other  .  w  );      }   }   // Graph class represents a directed graph   // using adjacency list representation   public     class     Graph     {      private     int     V  ;     // No. of vertices      private     List   <  int  >  []     adj  ;      private     List   <  Edge  >     edges  ;      public     Graph  (  int     v  )     // Constructor      {      V     =     v  ;      adj     =     new     List   <  int  >  [     v     ];      for     (  int     i     =     0  ;     i      <     v  ;     i  ++  )      adj  [  i  ]     =     new     List   <  int  >  ();      edges     =     new     List   <  Edge  >  ();      }      // function to Add an edge      public     void     AddEdge  (  int     u       int     v       int     w  )      {      adj  [  u  ].  Add  (  v  );     // Add w to v’s list.      adj  [  v  ].  Add  (  u  );     // Add w to v’s list.      edges  .  Add  (  new     Edge  (  u       v       w  ));      }      // function to perform dfs      private     void     DFS  (  int     v       bool  []     visited  )      {      // Mark the current node as visited and print it      visited  [  v  ]     =     true  ;      // Recur for all the vertices adjacent to      // this vertex      foreach  (  int     i     in     adj  [  v  ])      {      if     (  !  visited  [  i  ])      DFS  (  i       visited  );      }      }      // Returns true if given graph is connected else false      private     bool     IsConnected  ()      {      bool  []     visited     =     new     bool  [  V  ];      // Find all reachable vertices from first vertex      DFS  (  0       visited  );      // If set of reachable vertices includes all      // return true.      for     (  int     i     =     1  ;     i      <     V  ;     i  ++  )     {      if     (  visited  [  i  ]     ==     false  )      return     false  ;      }      return     true  ;      }      // This function assumes that edge (u v)      // exists in graph or not      public     void     ReverseDeleteMST  ()      {      // Sort edges in increasing order on basis of cost      edges  .  Sort  ();      int     mst_wt     =     0  ;     // Initialize weight of MST      Console  .  WriteLine  (  'Edges in MST'  );      // Iterate through all sorted edges in      // decreasing order of weights      for     (  int     i     =     edges  .  Count     -     1  ;     i     >=     0  ;     i  --  )     {      int     u     =     edges  [  i  ].  u  ;      int     v     =     edges  [  i  ].  v  ;      // Remove edge from undirected graph      adj  [  u  ].  Remove  (  v  );      adj  [  v  ].  Remove  (  u  );      // Adding the edge back if removing it      // causes disconnection. In this case this      // edge becomes part of MST.      if     (  IsConnected  ()     ==     false  )     {      adj  [  u  ].  Add  (  v  );      adj  [  v  ].  Add  (  u  );      // This edge is part of MST      Console  .  WriteLine  (  '({0} {1})'       u       v  );      mst_wt     +=     edges  [  i  ].  w  ;      }      }      Console  .  WriteLine  (  'Total weight of MST is {0}'        mst_wt  );      }   }   class     GFG     {      // Driver code      static     void     Main  (  string  []     args  )      {      // create the graph given in above figure      int     V     =     9  ;      Graph     g     =     new     Graph  (  V  );      // making above shown graph      g  .  AddEdge  (  0       1       4  );      g  .  AddEdge  (  0       7       8  );      g  .  AddEdge  (  1       2       8  );      g  .  AddEdge  (  1       7       11  );      g  .  AddEdge  (  2       3       7  );      g  .  AddEdge  (  2       8       2  );      g  .  AddEdge  (  2       5       4  );      g  .  AddEdge  (  3       4       9  );      g  .  AddEdge  (  3       5       14  );      g  .  AddEdge  (  4       5       10  );      g  .  AddEdge  (  5       6       2  );      g  .  AddEdge  (  6       7       1  );      g  .  AddEdge  (  6       8       6  );      g  .  AddEdge  (  7       8       7  );      g  .  ReverseDeleteMST  ();      }   }   // This code is contributed by cavi4762   
  JavaScript      // Javascript program to find Minimum Spanning Tree   // of a graph using Reverse Delete Algorithm   // Graph class represents a directed graph   // using adjacency list representation   class     Graph     {      // Constructor      constructor  (  V  )     {      this  .  V     =     V  ;      this  .  adj     =     [];      this  .  edges     =     [];      for     (  let     i     =     0  ;     i      <     V  ;     i  ++  )     {      this  .  adj  [  i  ]     =     [];      }      }          // function to add an edge to graph      addEdge  (  u       v       w  )     {      this  .  adj  [  u  ].  push  (  v  );  // Add w to v’s list.      this  .  adj  [  v  ].  push  (  u  );  // Add w to v’s list.      this  .  edges  .  push  ([  w       [  u       v  ]]);      }      DFS  (  v       visited  )     {      // Mark the current node as visited and print it      visited  [  v  ]     =     true  ;      for     (  const     i     of     this  .  adj  [  v  ])     {      if     (  !  visited  [  i  ])     {      this  .  DFS  (  i       visited  );      }      }      }      // Returns true if given graph is connected else false      isConnected  ()     {      const     visited     =     [];      for     (  let     i     =     0  ;     i      <     this  .  V  ;     i  ++  )     {      visited  [  i  ]     =     false  ;      }          // Find all reachable vertices from first vertex      this  .  DFS  (  0       visited  );          // If set of reachable vertices includes all      // return true.      for     (  let     i     =     1  ;     i      <     this  .  V  ;     i  ++  )     {      if     (  !  visited  [  i  ])     {      return     false  ;      }      }      return     true  ;      }      // This function assumes that edge (u v)      // exists in graph or not      reverseDeleteMST  ()     {          // Sort edges in increasing order on basis of cost      this  .  edges  .  sort  ((  a       b  )     =>     a  [  0  ]     -     b  [  0  ]);          let     mstWt     =     0  ;  // Initialize weight of MST          console  .  log  (  'Edges in MST'  );          // Iterate through all sorted edges in      // decreasing order of weights      for     (  let     i     =     this  .  edges  .  length     -     1  ;     i     >=     0  ;     i  --  )     {      const     [  u       v  ]     =     this  .  edges  [  i  ][  1  ];          // Remove edge from undirected graph      this  .  adj  [  u  ]     =     this  .  adj  [  u  ].  filter  (  x     =>     x     !==     v  );      this  .  adj  [  v  ]     =     this  .  adj  [  v  ].  filter  (  x     =>     x     !==     u  );          // Adding the edge back if removing it      // causes disconnection. In this case this       // edge becomes part of MST.      if     (  !  this  .  isConnected  ())     {      this  .  adj  [  u  ].  push  (  v  );      this  .  adj  [  v  ].  push  (  u  );          // This edge is part of MST      console  .  log  (  `(  ${  u  }     ${  v  }  )`  );      mstWt     +=     this  .  edges  [  i  ][  0  ];      }      }      console  .  log  (  `Total weight of MST is   ${  mstWt  }  `  );      }   }   // Driver code   function     main  ()   {      // create the graph given in above figure      var     V     =     9  ;      var     g     =     new     Graph  (  V  );      // making above shown graph      g  .  addEdge  (  0       1       4  );      g  .  addEdge  (  0       7       8  );      g  .  addEdge  (  1       2       8  );      g  .  addEdge  (  1       7       11  );      g  .  addEdge  (  2       3       7  );      g  .  addEdge  (  2       8       2  );      g  .  addEdge  (  2       5       4  );      g  .  addEdge  (  3       4       9  );      g  .  addEdge  (  3       5       14  );      g  .  addEdge  (  4       5       10  );      g  .  addEdge  (  5       6       2  );      g  .  addEdge  (  6       7       1  );      g  .  addEdge  (  6       8       6  );      g  .  addEdge  (  7       8       7  );      g  .  reverseDeleteMST  ();   }   main  ();   
    
  산출   Edges in MST (3 4) (0 7) (2 3) (2 5) (0 1) (5 6) (2 8) (6 7) Total weight of MST is 37  
     시간 복잡도: O((E*(V+E)) + E log E)    여기서 E는 모서리 수입니다.  
      공간 복잡도: O(V+E)    여기서 V는 정점 수이고 E는 가장자리 수입니다. 그래프를 저장하기 위해 인접 목록을 사용하므로 O(V+E)에 비례하는 공간이 필요합니다.  
      참고 사항:     
    위의 구현은 역삭제 알고리즘의 단순/순진한 구현이며 O(E log V(log log V)로 최적화될 수 있습니다.  ³ ) [원천 :    일주일    ]. 그러나 이 최적화된 시간 복잡도는 여전히    꼼꼼한    그리고    크루스칼    MST 알고리즘.  
  위의 구현은 원본 그래프를 수정합니다. 원본 그래프를 유지해야 하는 경우 그래프의 복사본을 만들 수 있습니다.  
 
     
         퀴즈 만들기