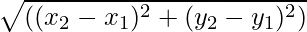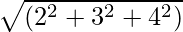벡터의 크기

벡터량은 방향과 크기를 모두 갖는 양입니다. 벡터의 크기는 벡터의 길이입니다. 이는 벡터의 숫자 값으로 제공되며 벡터의 길이를 나타내므로 항상 양수입니다. 모든 벡터에 대해 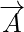overrightarrow{A} 그 크기는 다음과 같이 표현된다. .

이 기사에서 벡터의 크기, 공식, 예 및 기타 사항에 대해 자세히 알아 보겠습니다.

내용의 테이블

벡터의 크기는 무엇입니까?
벡터 공식의 크기
벡터의 방향
벡터의 크기를 찾는 방법은 무엇입니까?
해결된 예

벡터의 크기는 무엇입니까?

벡터의 크기는 벡터의 길이로 정의됩니다. 벡터의 크기는 벡터의 길이를 나타내므로 항상 양수입니다. 임의의 벡터 A에 대해 그 크기는 |A|로 표시됩니다. 벡터가 xi + yj로 정의되고 그 크기가 개별 항의 제곱합의 제곱근으로 정의된다고 가정합니다. 벡터의 크기는 벡터의 길이, 즉 벡터가 갖는 가치나 영향을 나타냅니다.

예를 들어, 5i N의 힘이 물체에 작용하면 그 크기는 5 N이 되며, 이는 적용된 힘의 강도가 5 N임을 의미합니다. 나' 5i에서는 양의 x 방향으로 적용됨을 나타냅니다.

벡터 공식의 크기

벡터의 크기를 계산하는 방법에는 여러 가지가 있습니다. 주어진 데이터를 바탕으로 다른 종류의 공식을 사용하여 벡터의 크기를 구합니다. 벡터 A의 크기는 모듈러스 연산자(예: |A|)를 사용하여 표현됩니다.

벡터의 크기를 계산하는 데 사용되는 다양한 공식이 있습니다. 다음 이미지는 벡터의 크기를 찾는 데 사용되는 중요한 공식을 보여줍니다.

다음은 크기를 계산하는 방법입니다.

벡터 Ā = xi+ yĵ + zk̂가 주어지면 벡터 Ā의 크기는 아래 공식을 사용하여 계산할 수 있습니다.

벡터의 크기 Ā (|A|) = √(x ² + 및 ² +z ² )

시작점 벡터가 (x ₁ , 그리고 ₁ ) 그리고 벡터의 끝점은 (x ₂ , 그리고 ₂ )가 주어지면 벡터의 크기가 주어집니다. 에 의해 주어진다,

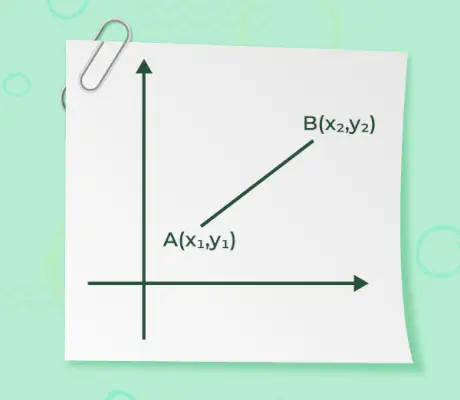
벡터의 시작과 끝점이 주어지면 벡터의 크기는 점 사이의 거리에 지나지 않습니다. 크기를 구하는 공식은 다음과 같습니다.

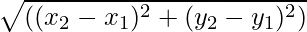
= $sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}$

벡터의 시작점이나 끝점 중 하나가 원점 o(0, 0)에 있고 다른 점이 에이(엑스,와이) 아래 그림에 지정된 것처럼

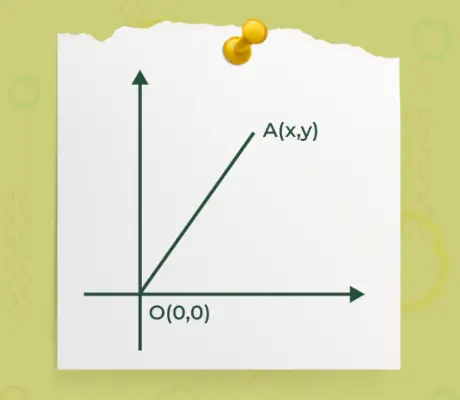
그런 다음 벡터의 끝 중 하나가 원점에 있는 벡터의 크기를 찾는 공식은 다음과 같습니다.

|Ā| = √(엑스 ² +y ² )

벡터의 방향

벡터량은 크기와 방향을 모두 갖는 양입니다. 벡터량의 방향은 벡터량이 어느 방향으로 적용되는지를 나타냅니다. 벡터가 수평선 또는 x축과 이루는 각도로 정의됩니다. 기호로 표현됩니다 ㅏ .

아래 이미지는 벡터의 방향을 표시하는 데 사용되는 화살표를 보여줍니다.

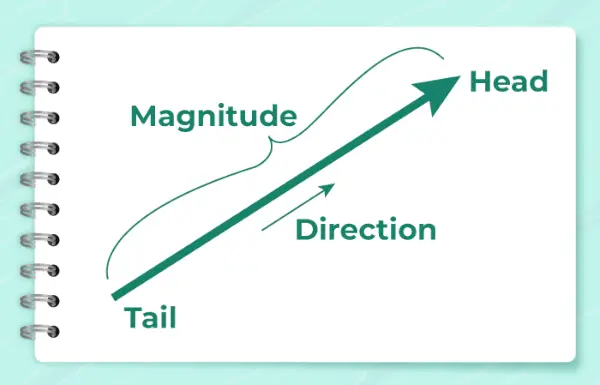
공식을 사용하여 계산됩니다.

α = 황갈색 ^-1 (y/x)

좌표(x)에 의해 생성된 벡터의 경우 ₁ , 그리고 ₁ ) 및 (x ₂ , 그리고 ₂ ) 그들의 방향은 공식으로 주어집니다.

α = 황갈색 ^-1 [(그리고 ₂ - 그리고 ₁ )/(엑스 ₂ – 엑스 ₁ )]

벡터의 크기를 찾는 방법은 무엇입니까?

벡터의 크기는 아래에 설명된 단계를 사용하여 계산됩니다.

1 단계: 벡터의 x, y, z 구성요소를 식별합니다.

2 단계 : 모든 x, y, z 구성요소의 제곱을 구합니다.

3단계: 2단계에서 찾은 정사각형을 모두 추가하세요.

4단계: 3단계에서 얻은 합의 제곱근을 구합니다.

4단계 이후에 얻은 값은 주어진 벡터의 크기입니다.

예: 벡터 A = 3i + 4j의 크기 찾기

해결책:

벡터 A의 크기는 위에서 설명한 단계를 사용하여 계산됩니다.

1 단계: A = 3i + 4j를 xi + yj와 비교하면 x = 3, y = 4가 됩니다.

2 단계: 엑스 ² = 3 ² = 9와 y ² = 4 ² = 16

3단계: 엑스 ² + 및 ² = 9 + 16 = 25

4단계: √(25) = 5

따라서 벡터 A = 3i + 4j의 크기는 5 단위입니다.

결론

결론적으로, 벡터의 크기는 벡터의 길이를 알려줍니다. 이 개념은 속도, 힘, 이동 방향 등을 측정하는 데 도움이 되기 때문에 물리학, 공학, 컴퓨터 과학과 같은 많은 분야에서 매우 중요합니다. 벡터 크기를 이해함으로써 실제 문제를 더 잘 분석하고 해결할 수 있으므로 실제 응용 프로그램에서 숫자 및 측정 작업을 수행하는 모든 사람에게 핵심 지식이 됩니다.

더 읽어보기,

스칼라와 벡터

벡터 연산

단위 벡터를 계산하는 방법은 무엇입니까?

벡터의 크기에 대한 해결된 예

예 1: 벡터 Ā = 2i + 3ĵ + 4k의 크기를 구합니다.

해결책:

주어진,

Ā = 2i + 3ĵ + 4k

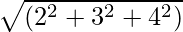
크기 |A| = $sqrt{(2^2+3^2+4^2)}$

=
= √29
= 5.38

벡터의 크기 2i+3ĵ+4k ~이다 5.38 단위

예 2: 벡터 Ā = 3i + 3ĵ – 6k의 크기 찾기

해결책:

주어진

Ā = 3i + 3ĵ – 6k

크기 |A| = $sqrt{(3^2+3^2+(-6)^2)}$

=
= √54
= 7.35

벡터의 크기 3i+ 3ĵ – 6k ~이다 7.35 단위.

예 3: 벡터의 시작점이 (3, 4)이고 끝점이 (6, 2)인 경우 벡터의 크기를 구합니다.

해결책:

주어진,

(엑스 ₁ , 그리고 ₁ ) = (3, 4)
(엑스 ₂ , 그리고 ₂ ) = (6, 2)

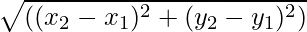
|Ā|= $sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}$

= $sqrt{((6-3)^2+(2-4)^2)}$
= √(3 ² + (-2) ² )
= √(9+4)
= √13 = 3.6

따라서 주어진 벡터의 크기는 다음과 같습니다. 3.6 단위.

예 4: 벡터의 시작점이 (2, 1, 4)이고 끝점이 (5, 2, 6)인 경우 벡터의 크기를 구합니다.

해결책:

주어진,

(엑스 ₁ , 그리고 ₁ , 와 함께 ₁ ) = (2, 1, 4)

(엑스 ₂ , 그리고 ₂ , 와 함께 ₂ ) = (5, 2, 6)

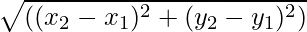
|Ā| = $sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}$

= $sqrt{((5-2)^2+(2-1)^2+(6-4)^2)}$
=
= √(9 +1 + 4)
= √14 = 3.74

따라서 주어진 벡터의 크기는 다음과 같습니다. 3.74 단위.

예제 5: 원점에서 시작하고 (3, 4)의 끝점에서 시작하는 벡터의 크기는 얼마입니까?

해결책:

주어진,

벡터의 시작점은 O(0, 0)입니다.

끝점(x, y) = (3, 4)

벡터의 크기(|Ā|) = √(x ² +y ² )

= √(3 ² + 4 ² )
= √(9 + 16)
= √25 = 5

따라서 주어진 벡터의 크기는 다음과 같습니다. 5 단위.

예제 6: 끝점 중 하나가 원점에 있고 다른 점이 (1, 4, 3)에 있는 벡터의 크기를 구합니다.

해결책:

주어진,

벡터의 끝점은 O(0, 0)입니다.

다른 점(x, y, z) = (1, 4, 3)

벡터의 크기(|Ā|) = √(x ² +y ² +z ² )

= $sqrt{(1^2+4^2+3^2)}$
=
= √26 = 5.09

따라서 주어진 벡터의 크기는 다음과 같습니다. 5.09 단위.

벡터 크기에 대한 FAQ

벡터 공식의 크기는 얼마입니까?

벡터의 크기는 벡터의 숫자 값이며 벡터의 길이를 정의합니다. 모든 벡터에 대해 A의 크기는 |A|로 표시됩니다. 벡터의 크기는 다음 공식을 사용하여 계산됩니다.

모든 벡터에 대해 A = xi + yj + zk의 크기는 다음 공식으로 제공됩니다.

|아| = √(엑스 ² + 및 ² + z ² )

시작점과 끝점이 각각 (x ₁ , 그리고 ₁ ) 및 (x ₂ , 그리고 ₂ ) 그 크기는 공식에 의해 주어진다

|아| = √((x ₂ – 엑스 ₁ ) ² + (그리고 ₂ - 그리고 ₁ ) ² )

벡터의 크기를 어떻게 표현하나요?

벡터의 크기 ㅏ 기호 |A|로 표시됩니다.

벡터의 크기를 찾는 방법은 무엇입니까?

벡터의 크기를 계산하기 위해 다양한 공식이 사용됩니다.

|아| = √(엑스 ² + 및 ² + z ² ) 벡터가 A = xi + yj + zk 형식인 경우

|아| = √((x) ² + (그리고) ² ) 벡터가 점 A(x, y)와 원점 O(0, 0)으로 주어질 때.

|아| = √((x ₂ – 엑스 ₁ ) ² + (그리고 ₂ - 그리고 ₁ ) ² ) 벡터가 점 A(x ₁ , 그리고 ₂ ) 및 점 B(x ₂ , 그리고 ₂ ).