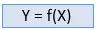a ² – б ² формула в Алгебра це основна формула в математиці, яка використовується для розв'язування різноманітних алгебраїчних задач. a ² – б ² Формула також називається формулою різниці квадратів, оскільки ця формула допомагає нам знайти різницю між двома квадратами без фактичного обчислення квадратів. На зображенні, доданому нижче, показано формулу a ² – б ²

У цій статті ми дізнаємося про a ² – б ² формула, а ² – б ² ідентичність, приклади та ін.

Зміст

• Що таке формула a2 – b2?
• Формула різниці квадратів
• a2 – b2 Доказ формули квадрата
• Формули (a + b)2 і (a – b)2
• a2 – b2 Тотожність

Що таке a ² – б ² Формула?

a ² – б ² формула в алгебрі — основна формула для розв'язування алгебраїчних задач. Він також використовується для вирішення тригонометричних, диференціальних та інших задач. Ця формула говорить нам, що різниця між квадратом двох чисел дорівнює добутку суми та різниці двох чисел, тобто

a ² – б ² = (a + b).(a – b)

a ² – б ² Визначення формули

Формула а ² – б ² дозволяє нам визначити дисперсію між квадратами двох чисел без необхідності обчислювати фактичні значення квадратів. Вираз для a ² – б ² формула виглядає наступним чином: a ² – б ² = (a + b).(a – b)

Формула різниці квадратів

Різниця двох квадратів обчислюється за допомогою стандартної алгебраїчної тотожності a ² – б ² . Наприклад, нам дано дві змінні, a і b, тоді різниця їх квадратів обчислюється за формулою, a ² – б ² = (a+b).(a–b)

По суті, формула різниці квадратів говорить, що для будь-яких двох алгебраїчних змінних a і b вираз a ² – б ² дорівнює добутку суми та різниці змінних. Ця тотожність широко використовується для спрощення складних алгебраїчних виразів.

a ² – б ² Доказ формули квадрата

a ² – б ² тотожність можна підтвердити шляхом спрощення RHS тотожності. А ² – б ² формула подається як,

a ² – б ² = (a – b)(a + b)

Ця формула доведена як

RHS = (a+b) (a–b)

⇒ RHS = a (a–b) + b (a–b)

⇒ RHS = a ² – ab + ba – b ²

⇒ RHS = a ² – ab + ab – b ²

⇒ RHS = a ² – б ²

⇒ RHS = LHS

Отже, доведено.

a ² + б ² Формула

А ² + б ² формула — це алгебраїчна формула, яка використовується для знаходження суми квадратів двох чисел. Сума квадратної формули подається як

a ² + б ² = (a + b) ² – 2ab

А ² + б ² Формула використовується для вирішення різних алгебраїчних задач. Нижче додано інші важливі алгебраїчні формули,

(а + б) ² і (а – б) ² Формула

(a + b) ² формула подається як,

(а + б) ² = а ² + б ² + 2ab

(а – б) ² формула подається як,

(а – б) ² = а ² + б ² – 2ab

a ² – б ² Ідентичність

a ² – б ² ідентичність є одним із алгебраїчні тотожності який використовується для знаходження різниці між квадратами двох чисел. Ця ідентичність має різні застосування та подається як,

a ² – б ² = (a – b).(a + b)

Детальніше,

• Формула алгебри
• Основна математична формула
• Алгебричний вираз

Приклади на а ² – б ² Формула

Приклад 1: спростіть x ² – 16

рішення:

= х ² – 16

= х ² - 4 ²

ми це знаємо, a ² – б ² = (a+b) (a–b)

враховуючи,

• a = x
• b = 4

= (x + 4)(x – 4)

Приклад 2: спростіть 9y ² – 144

рішення:

= 9 років ² – 144

= (3 роки) ² – (12) ²

ми це знаємо, a ² – б ² = (a+b)(a–b)

враховуючи,

• a = 3y
• b = 12

= (3y + 12)(3y – 12)

Приклад 3: Спрощення (3x + 2) ² – (3x – 2) ²

рішення:

ми це знаємо,

a ² – б ² = (a+b)(a–b)

враховуючи,

• a = 3x + 2
• b = 3x – 2

(3x + 2) ² – (3x – 2) ²

= (3x + 2 + 3x – 2)(3x + 2 – (3x – 2))

= 6x(3x + 2 – 3x + 2)

= 6x(4)

= 24x

Приклад 4: Спростіть і ² – 100

рішення:

= і ² – 100

= і ² – (10) ²

ми це знаємо,

a ² – б ² = (a+b)(a–b)

враховуючи,

• а = і
• b = 10

= (y + 10) (y – 10)

Приклад 5: обчислення (x + 6) (x – 6)

рішення:

ми це знаємо,

(a+b) (a–b) = a ² – б ²

враховуючи,

• a = x
• b = 6

(x + 6) (x – 6)

= х ² – 6 ²

= х ² – 36

Приклад 6: обчислення (y + 13)(y – 13)

рішення:

ми це знаємо,

(a+b) (a–b) = a ² – б ²

враховуючи,

• а = і
• b = 13

(у + 13).(у – 13)

= і ² – (13) ²

= і ² – 169

Приклад 7: обчисліть (x + y + z). (x + y – z)

рішення:

ми це знаємо,

(a+b) (a–b) = a ² – б ²

враховуючи,

• a = x + y
• b = z

(x + y + z) (x + y – z)

= (x + y) ² - З ²

= х ² + і ² + 2xy – z ²

(а ² – б ² ) Формула – робочий лист

Q1. Спростіть 15 ² – 14 ² використовуючи a ² – б ² ідентичність.

Q2. Спростіть 11 ² – 7 ² використовуючи a ² – б ² ідентичність.

Q3. Розв'язати 23 ² – 9 ² використовуючи a ² – б ² ідентичність.

Q4. Розв'язати 9 ² – 7 ² використовуючи a ² – б ² ідентичність.

a ² – б ² Формула – поширені запитання

1. Що таке a ² − б ² ?

a ² – б ² формула — це формула, яка використовується для знаходження різниці між двома квадратами без фактичного знаходження квадрата. А ² – б ² формула,

a ² – б ² = (a + b)(a – b)

2. Що таке закон a ² b ² Формула?

Закон а ² b ² формули,

• a ² – б ² = (a + b)(a – b)
• a ² + б ² = (a + b) ² – 2ab

3. Що таке a ² b ² Формула, яка використовується для?

a ² b ² формули використовуються для розв’язування різних алгебраїчних задач, вони також використовуються для спрощення тригонометричних задач, задач числення та інтегрування.

4. Що таке a ² b ² Формула?

Є два а ² b ² формули, які є, a ² + б ² , і a ² – б ² формула розкладання для a ² b ² формули подано як,

• a ² – б ² = (a + b)(a – b)
• a ² + б ² = (a + b) ² – 2ab

5. Коли а ² – б ² Використовується формула?

a ² – б ² формула використовується для знаходження різниці між квадратами двох чисел без фактичного знаходження квадратів. Ця формула також використовується для розв'язування різноманітних алгебраїчних, тригонометричних та інших задач.