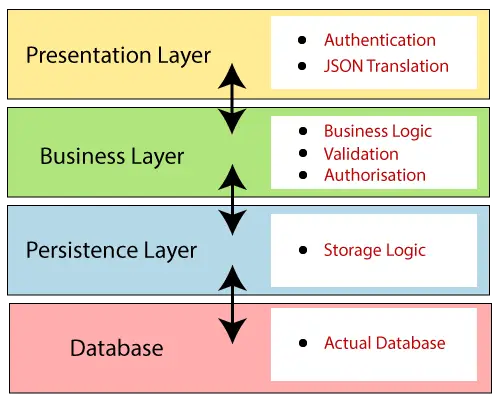
Композиція відносин

Нехай A, B і C — множини, R — відношення від A до B і S — відношення від B до C. Тобто R є підмножиною A × B, а S — підмножиною B × C. Тоді R і S породжують відношення від A до C, позначене R◦S і визначене:
a (R◦S)c if for some b ∈ B we have aRb and bSc. That is, R ◦ S = there exists b ∈ B for which (a, b) ∈ R and (b, c) ∈ S
Відношення R◦S є відомим складом R і S; іноді його позначають просто RS.
Нехай R є відношенням на множині A, тобто R є відношенням множини A до самого себе. Тоді R◦R, композиція R із собою, завжди представлена. Також R◦R іноді позначають R 2 . Так само Р 3 = Р 2 ◦R = R◦R◦R і так далі. Таким чином Р п визначається для всіх позитивних n.
Приклад 1: Нехай X = {4, 5, 6}, Y = {a, b, c} і Z = {l, m, n}. Розглянемо відношення R 1 від X до Y і R 2 від Y до Z.
R<sub>1</sub> = {(4, a), (4, b), (5, c), (6, a), (6, c)} R<sub>2</sub> = {(a, l), (a, n), (b, l), (b, m), (c, l), (c, m), (c, n)} 
Знайти склад відношення (і) Р 1 Р 2 (іі) Р 1 Р 1 -1
рішення:
(i) Відношення складу R 1 Р 2 як показано на рис.

Р 1 Р 2 = {(4, l), (4, n), (4, m), (5, l), (5, m), (5, n), (6, l), (6, m), (6, n)}
(ii) Композиційне відношення R 1 Р 1 -1 як показано на рис.

Р 1 Р 1 -1 = {(4, 4), (5, 5), (5, 6), (6, 4), (6, 5), (4, 6), (6, 6)}
Композиція відношень і матриць
Існує інший спосіб знайти R◦S. Нехай М Р і М С позначають відповідно матричні зображення відношень R і S. Тоді
приклад
Let P = {2, 3, 4, 5}. Consider the relation R and S on P defined by R = {(2, 2), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5), (5, 3)} S = {(2, 3), (2, 5), (3, 4), (3, 5), (4, 2), (4, 3), (4, 5), (5, 2), (5, 5)}. Find the matrices of the above relations. Use matrices to find the following composition of the relation R and S. (i)RoS (ii)RoR (iii)SoR рішення: Матриці відношення R і S показані на рис.

(i) Щоб отримати композицію відношення R і S. Спочатку помножте M Р з М С щоб отримати матрицю M Р х М С як показано на рис.
Ненульові елементи в матриці M Р х М С розповідає елементи, пов'язані в RoS. Так,

Отже, композиція R o S відношення R і S є
R o S = {(2, 2), (2, 3), (2, 4), (3, 2), (3, 3), (4, 2), (4, 5), (5, 2), (5, 3), (5, 4), (5, 5)}. (ii) Спочатку помножте матрицю M Р сам по собі, як показано на рис

Отже, композиція R або R відношення R і S є
R o R = {(2, 2), (3, 2), (3, 3), (3, 4), (4, 2), (4, 5), (5, 2), (5, 3), (5, 5)} (iii) Помножте матрицю M С з М Р щоб отримати матрицю M С х М Р як показано на рис.

Ненульові елементи в матриці M С х М Р розповідає елементи, пов’язані в S o R.
Отже, композиція S o R відношення S і R є
S o R = {(2, 4) , (2, 5), (3, 3), (3, 4), (3, 5), (4, 2), (4, 4), (4, 5), (5, 2), (5, 3), (5, 4), (5, 5)}.