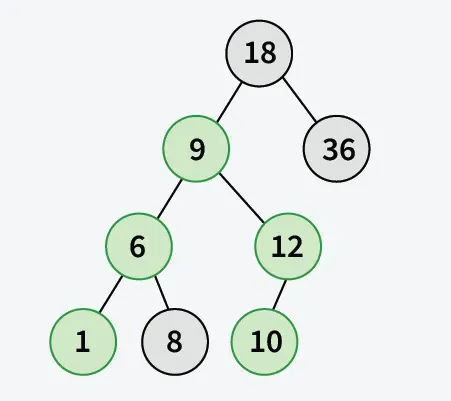
Minsta kostnadsväg med drag åt vänster, höger, botten och uppåt tillåtna


Givet ett 2D-rutnät av storlek n*n där varje cell representerar kostnaden för att gå igenom den cellen är uppgiften att hitta lägsta kostnad att flytta från uppe till vänster cell till längst ner till höger cell. Från en given cell kan vi flytta in 4 vägbeskrivningar : vänster höger upp och ner.
Notera: Det antas att negativa kostnadscykler inte finns i inmatningsmatrisen.
Exempel:
Input: rutnät = {{9 4 9 9}
{6 7 6 4}
{8 3 3 7}
{7 4 9 10}}
Utgång: 43
Förklaring: Minsta kostnadsväg är 9 + 4 + 7 + 3 + 3 + 7 + 10.
Närma sig:
Tanken är att använda Dijkstras algoritm för att hitta minimikostnadsvägen genom nätet. Detta tillvägagångssätt behandlar rutnätet som en graf där varje cell är en nod och algoritmen utforskar dynamiskt den mest kostnadseffektiva vägen till den nedre högra cellen genom att alltid expandera de lägsta kostnadsvägarna först.
Steg för steg tillvägagångssätt:
- Använd en min-hög för att alltid bearbeta den lägsta kostnadsvägen först och tryck in den övre vänstra cellen i den.
- Initiera en kostnadsmatris med maximala värden som ställer in startcellens kostnad till dess rutnätsvärde.
- Kontrollera alla 4 närliggande celler för varje cell
- Om en lägre kostnadsväg hittas uppdaterar du kostnaden för cellen och skjuter den till högen.
- Returnera minimikostnaden för att nå den nedre högra cellen.
Nedan är implementeringen av ovanstående tillvägagångssätt:
C++ // C++ program to find minimum Cost Path with // Left Right Bottom and Up moves allowed #include using namespace std ; // Function to check if cell is valid. bool isValidCell ( int i int j int n ) { return i >= 0 && i < n && j >= 0 && j < n ; } int minimumCostPath ( vector < vector < int >> & grid ) { int n = grid . size (); // Min heap to implement dijkstra priority_queue < vector < int > vector < vector < int >> greater < vector < int >>> pq ; // 2d grid to store minimum cost // to reach every cell. vector < vector < int >> cost ( n vector < int > ( n INT_MAX )); cost [ 0 ][ 0 ] = grid [ 0 ][ 0 ]; // Direction vector to move in 4 directions vector < vector < int >> dir = {{ -1 0 } { 1 0 } { 0 -1 } { 0 1 }}; pq . push ({ grid [ 0 ][ 0 ] 0 0 }); while ( ! pq . empty ()) { vector < int > top = pq . top (); pq . pop (); int c = top [ 0 ] i = top [ 1 ] j = top [ 2 ]; // Check for all 4 neighbouring cells. for ( auto d : dir ) { int x = i + d [ 0 ]; int y = j + d [ 1 ]; // If cell is valid and cost to reach this cell // from current cell is less if ( isValidCell ( x y n ) && cost [ i ][ j ] + grid [ x ][ y ] < cost [ x ][ y ]) { // Update cost to reach this cell. cost [ x ][ y ] = cost [ i ][ j ] + grid [ x ][ y ]; // Push the cell into heap. pq . push ({ cost [ x ][ y ] x y }); } } } // Return minimum cost to // reach bottom right cell. return cost [ n -1 ][ n -1 ]; } int main () { vector < vector < int >> grid = {{ 9 4 9 9 }{ 6 7 6 4 }{ 8 3 3 7 }{ 7 4 9 10 }}; cout < < minimumCostPath ( grid ) < < endl ; return 0 ; }
Java // Java program to find minimum Cost Path with // Left Right Bottom and Up moves allowed import java.util.PriorityQueue ; import java.util.Arrays ; class GfG { // Function to check if cell is valid. static boolean isValidCell ( int i int j int n ) { return i >= 0 && i < n && j >= 0 && j < n ; } static int minimumCostPath ( int [][] grid ) { int n = grid . length ; // Min heap to implement Dijkstra PriorityQueue < int []> pq = new PriorityQueue <> (( a b ) -> Integer . compare ( a [ 0 ] b [ 0 ] )); // 2D grid to store minimum cost // to reach every cell. int [][] cost = new int [ n ][ n ] ; for ( int [] row : cost ) { Arrays . fill ( row Integer . MAX_VALUE ); } cost [ 0 ][ 0 ] = grid [ 0 ][ 0 ] ; // Direction vector to move in 4 directions int [][] dir = {{ - 1 0 } { 1 0 } { 0 - 1 } { 0 1 }}; pq . offer ( new int [] { grid [ 0 ][ 0 ] 0 0 }); while ( ! pq . isEmpty ()) { int [] top = pq . poll (); int c = top [ 0 ] i = top [ 1 ] j = top [ 2 ] ; // Check for all 4 neighbouring cells. for ( int [] d : dir ) { int x = i + d [ 0 ] ; int y = j + d [ 1 ] ; // If cell is valid and cost to reach this cell // from current cell is less if ( isValidCell ( x y n ) && cost [ i ][ j ] + grid [ x ][ y ] < cost [ x ][ y ] ) { // Update cost to reach this cell. cost [ x ][ y ] = cost [ i ][ j ] + grid [ x ][ y ] ; // Push the cell into heap. pq . offer ( new int [] { cost [ x ][ y ] x y }); } } } // Return minimum cost to // reach bottom right cell. return cost [ n - 1 ][ n - 1 ] ; } public static void main ( String [] args ) { int [][] grid = { { 9 4 9 9 } { 6 7 6 4 } { 8 3 3 7 } { 7 4 9 10 } }; System . out . println ( minimumCostPath ( grid )); } }
Python # Python program to find minimum Cost Path with # Left Right Bottom and Up moves allowed import heapq # Function to check if cell is valid. def isValidCell ( i j n ): return i >= 0 and i < n and j >= 0 and j < n def minimumCostPath ( grid ): n = len ( grid ) # Min heap to implement Dijkstra pq = [] # 2D grid to store minimum cost # to reach every cell. cost = [[ float ( 'inf' )] * n for _ in range ( n )] cost [ 0 ][ 0 ] = grid [ 0 ][ 0 ] # Direction vector to move in 4 directions dir = [[ - 1 0 ] [ 1 0 ] [ 0 - 1 ] [ 0 1 ]] heapq . heappush ( pq [ grid [ 0 ][ 0 ] 0 0 ]) while pq : c i j = heapq . heappop ( pq ) # Check for all 4 neighbouring cells. for d in dir : x y = i + d [ 0 ] j + d [ 1 ] # If cell is valid and cost to reach this cell # from current cell is less if isValidCell ( x y n ) and cost [ i ][ j ] + grid [ x ][ y ] < cost [ x ][ y ]: # Update cost to reach this cell. cost [ x ][ y ] = cost [ i ][ j ] + grid [ x ][ y ] # Push the cell into heap. heapq . heappush ( pq [ cost [ x ][ y ] x y ]) # Return minimum cost to # reach bottom right cell. return cost [ n - 1 ][ n - 1 ] if __name__ == '__main__' : grid = [ [ 9 4 9 9 ] [ 6 7 6 4 ] [ 8 3 3 7 ] [ 7 4 9 10 ] ] print ( minimumCostPath ( grid ))
C# // C# program to find minimum Cost Path with // Left Right Bottom and Up moves allowed using System ; using System.Collections.Generic ; class GfG { // Function to check if cell is valid. static bool isValidCell ( int i int j int n ) { return i >= 0 && i < n && j >= 0 && j < n ; } static int minimumCostPath ( int [][] grid ) { int n = grid . Length ; // Min heap to implement Dijkstra var pq = new SortedSet < ( int cost int x int y ) > (); // 2D grid to store minimum cost // to reach every cell. int [][] cost = new int [ n ][]; for ( int i = 0 ; i < n ; i ++ ) { cost [ i ] = new int [ n ]; Array . Fill ( cost [ i ] int . MaxValue ); } cost [ 0 ][ 0 ] = grid [ 0 ][ 0 ]; // Direction vector to move in 4 directions int [][] dir = { new int [] { - 1 0 } new int [] { 1 0 } new int [] { 0 - 1 } new int [] { 0 1 } }; pq . Add (( grid [ 0 ][ 0 ] 0 0 )); while ( pq . Count > 0 ) { var top = pq . Min ; pq . Remove ( top ); int i = top . x j = top . y ; // Check for all 4 neighbouring cells. foreach ( var d in dir ) { int x = i + d [ 0 ]; int y = j + d [ 1 ]; // If cell is valid and cost to reach this cell // from current cell is less if ( isValidCell ( x y n ) && cost [ i ][ j ] + grid [ x ][ y ] < cost [ x ][ y ]) { // Update cost to reach this cell. cost [ x ][ y ] = cost [ i ][ j ] + grid [ x ][ y ]; // Push the cell into heap. pq . Add (( cost [ x ][ y ] x y )); } } } // Return minimum cost to // reach bottom right cell. return cost [ n - 1 ][ n - 1 ]; } static void Main ( string [] args ) { int [][] grid = new int [][] { new int [] { 9 4 9 9 } new int [] { 6 7 6 4 } new int [] { 8 3 3 7 } new int [] { 7 4 9 10 } }; Console . WriteLine ( minimumCostPath ( grid )); } }
JavaScript // JavaScript program to find minimum Cost Path with // Left Right Bottom and Up moves allowed function comparator ( a b ) { if ( a [ 0 ] > b [ 0 ]) return - 1 ; if ( a [ 0 ] < b [ 0 ]) return 1 ; return 0 ; } class PriorityQueue { constructor ( compare ) { this . heap = []; this . compare = compare ; } enqueue ( value ) { this . heap . push ( value ); this . bubbleUp (); } bubbleUp () { let index = this . heap . length - 1 ; while ( index > 0 ) { let element = this . heap [ index ] parentIndex = Math . floor (( index - 1 ) / 2 ) parent = this . heap [ parentIndex ]; if ( this . compare ( element parent ) < 0 ) break ; this . heap [ index ] = parent ; this . heap [ parentIndex ] = element ; index = parentIndex ; } } dequeue () { let max = this . heap [ 0 ]; let end = this . heap . pop (); if ( this . heap . length > 0 ) { this . heap [ 0 ] = end ; this . sinkDown ( 0 ); } return max ; } sinkDown ( index ) { let left = 2 * index + 1 right = 2 * index + 2 largest = index ; if ( left < this . heap . length && this . compare ( this . heap [ left ] this . heap [ largest ]) > 0 ) { largest = left ; } if ( right < this . heap . length && this . compare ( this . heap [ right ] this . heap [ largest ]) > 0 ) { largest = right ; } if ( largest !== index ) { [ this . heap [ largest ] this . heap [ index ]] = [ this . heap [ index ] this . heap [ largest ] ]; this . sinkDown ( largest ); } } isEmpty () { return this . heap . length === 0 ; } } // Function to check if cell is valid. function isValidCell ( i j n ) { return i >= 0 && i < n && j >= 0 && j < n ; } function minimumCostPath ( grid ) { let n = grid . length ; // Min heap to implement Dijkstra const pq = new PriorityQueue ( comparator ) // 2D grid to store minimum cost // to reach every cell. let cost = Array . from ({ length : n } () => Array ( n ). fill ( Infinity )); cost [ 0 ][ 0 ] = grid [ 0 ][ 0 ]; // Direction vector to move in 4 directions let dir = [[ - 1 0 ] [ 1 0 ] [ 0 - 1 ] [ 0 1 ]]; pq . enqueue ([ grid [ 0 ][ 0 ] 0 0 ]); while ( ! pq . isEmpty ()) { let [ c i j ] = pq . dequeue (); // Check for all 4 neighbouring cells. for ( let d of dir ) { let x = i + d [ 0 ]; let y = j + d [ 1 ]; // If cell is valid and cost to reach this cell // from current cell is less if ( isValidCell ( x y n ) && cost [ i ][ j ] + grid [ x ][ y ] < cost [ x ][ y ]) { // Update cost to reach this cell. cost [ x ][ y ] = cost [ i ][ j ] + grid [ x ][ y ]; // Push the cell into heap. pq . enqueue ([ cost [ x ][ y ] x y ]); } } } // Return minimum cost to // reach bottom right cell. return cost [ n - 1 ][ n - 1 ]; } let grid = [ [ 9 4 9 9 ] [ 6 7 6 4 ] [ 8 3 3 7 ] [ 7 4 9 10 ] ]; console . log ( minimumCostPath ( grid ));
Produktion
43
Tidskomplexitet: O(n^2 log(n^2))
Hjälputrymme: O(n^2 log(n^2))
Varför kan dynamisk programmering inte användas?
Dynamisk programmering misslyckas här eftersom att tillåta rörelse i alla fyra riktningarna skapar cykler där celler kan återbesökas och bryter det optimala antagandet om understruktur. Detta innebär att kostnaden för att nå en cell från en given cell inte är fast utan beror på hela vägen.
Relaterade artiklar:
Min kostnadsväg
Skapa frågesport