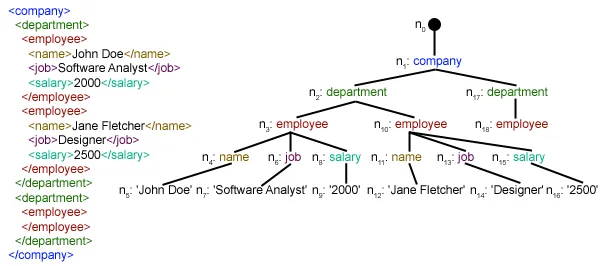
Problema de vendedor ambulante usando ramificação e limite

Dado um conjunto de cidades e distância entre todos os pares de cidades, o problema é encontrar a turnê mais curta possível que visita todas as cidades exatamente uma vez e retorna ao ponto de partida.

Por exemplo, considere o gráfico mostrado na figura no lado direito. Um passeio TSP no gráfico é 0-1-3-2-0. O custo do passeio é 10+25+30+15, que é 80.
Discutimos as seguintes soluções
1) Programação ingênua e dinâmica
2) Solução aproximada usando MST
Ramificação e solução ligada
Como visto nos artigos anteriores no método de ramificação e vinculado para o nó atual na árvore, calculamos um limite na melhor solução possível que podemos obter se diminuirmos esse nó. Se o limite da melhor solução possível é pior que o melhor atual (melhor calculado até agora), ignoramos a subárvore enraizada no nó.
Observe que o custo através de um nó inclui dois custos.
1) Custo de atingir o nó da raiz (quando atingimos um nó, temos esse custo calculado)
2) Custo de atingir uma resposta do nó atual para uma folha (calculamos um limite nesse custo para decidir se ignorará a subárvore com este nó ou não).
- Nos casos de um problema de maximização Um limite superior nos diz a solução máxima possível se seguirmos o nó fornecido. Por exemplo, em 0/1 Knapsack, usamos a abordagem gananciosa para encontrar um limite superior .
- Nos casos de um problema de minimização Um limite inferior nos diz a solução mínima possível se seguirmos o nó fornecido. Por exemplo, em Problema de atribuição de trabalho Temos um limite inferior ao atribuir menos custos a um trabalhador.
Na filial e vinculado, a parte desafiadora é descobrir uma maneira de calcular um limite na melhor solução possível. Abaixo está uma ideia usada para calcular os limites para o problema de vendedor ambulante.
O custo de qualquer turnê pode ser escrito como abaixo.
Cost of a tour T = (1/2) * ? (Sum of cost of two edges adjacent to u and in the tour T) where u ? V For every vertex u if we consider two edges through it in T and sum their costs. The overall sum for all vertices would be twice of cost of tour T (We have considered every edge twice.) (Sum of two tour edges adjacent to u) >= (sum of minimum weight two edges adjacent to u) Cost of any tour >= 1/2) * ? (Sum of cost of two minimum weight edges adjacent to u) where u ? V
Por exemplo, considere o gráfico mostrado acima. Abaixo estão o custo mínimo duas arestas adjacentes a todos os nós.
Node Least cost edges Total cost 0 (0 1) (0 2) 25 1 (0 1) (1 3) 35 2 (0 2) (2 3) 45 3 (0 3) (1 3) 45 Thus a lower bound on the cost of any tour = 1/2(25 + 35 + 45 + 45) = 75 Refer this for one more example.
Agora temos uma idéia sobre o cálculo do limite inferior. Vamos ver como aplicá -lo na árvore de busca de espaço estadual. Começamos a enumerar todos os nós possíveis (de preferência em ordem lexicográfica)
1. O nó raiz: Sem perda de generalidade, assumimos que começamos no vértice '0' para o qual o limite inferior foi calculado acima.
Lidar com o nível 2: O próximo nível enumera todos os vértices possíveis para os quais podemos ir (tendo em mente que em qualquer caminho um vértice deve ocorrer apenas uma vez) que são 1 2 3 ... n (observe que o gráfico está completo). Considere que estamos calculando para o Vertex 1 desde que passamos de 0 para 1 Nosso passeio incluiu agora o Edge 0-1. Isso nos permite fazer as alterações necessárias no limite inferior da raiz.
Lower Bound for vertex 1 = Old lower bound - ((minimum edge cost of 0 + minimum edge cost of 1) / 2) + (edge cost 0-1)
Como funciona? Para incluir a borda 0-1, adicionamos o custo da borda de 0-1 e subtraia um peso de borda, de modo que o limite inferior permaneça o mais apertado possível, que seria a soma das bordas mínimas de 0 e 1 divididas por 2. Claramente a borda subtraída não pode ser menor que isso.
Lidar com outros níveis: À medida que passamos para o próximo nível, enumeramos novamente todos os vértices possíveis. Para o caso acima que vai mais longe após 1, verificamos 2 3 4 ... n.
Considere o limite inferior para 2 à medida que passamos de 1 para 1, incluímos a borda 1-2 para o passeio e alteramos o novo limite inferior para este nó.
Lower bound(2) = Old lower bound - ((second minimum edge cost of 1 + minimum edge cost of 2)/2) + edge cost 1-2)
NOTA: A única alteração na fórmula é que, desta vez, incluímos o segundo custo mínimo da borda para 1 porque o custo mínimo da borda já foi subtraído no nível anterior.
// C++ program to solve Traveling Salesman Problem // using Branch and Bound. #include using namespace std ; const int N = 4 ; // final_path[] stores the final solution ie the // path of the salesman. int final_path [ N + 1 ]; // visited[] keeps track of the already visited nodes // in a particular path bool visited [ N ]; // Stores the final minimum weight of shortest tour. int final_res = INT_MAX ; // Function to copy temporary solution to // the final solution void copyToFinal ( int curr_path []) { for ( int i = 0 ; i < N ; i ++ ) final_path [ i ] = curr_path [ i ]; final_path [ N ] = curr_path [ 0 ]; } // Function to find the minimum edge cost // having an end at the vertex i int firstMin ( int adj [ N ][ N ] int i ) { int min = INT_MAX ; for ( int k = 0 ; k < N ; k ++ ) if ( adj [ i ][ k ] < min && i != k ) min = adj [ i ][ k ]; return min ; } // function to find the second minimum edge cost // having an end at the vertex i int secondMin ( int adj [ N ][ N ] int i ) { int first = INT_MAX second = INT_MAX ; for ( int j = 0 ; j < N ; j ++ ) { if ( i == j ) continue ; if ( adj [ i ][ j ] <= first ) { second = first ; first = adj [ i ][ j ]; } else if ( adj [ i ][ j ] <= second && adj [ i ][ j ] != first ) second = adj [ i ][ j ]; } return second ; } // function that takes as arguments: // curr_bound -> lower bound of the root node // curr_weight-> stores the weight of the path so far // level-> current level while moving in the search // space tree // curr_path[] -> where the solution is being stored which // would later be copied to final_path[] void TSPRec ( int adj [ N ][ N ] int curr_bound int curr_weight int level int curr_path []) { // base case is when we have reached level N which // means we have covered all the nodes once if ( level == N ) { // check if there is an edge from last vertex in // path back to the first vertex if ( adj [ curr_path [ level -1 ]][ curr_path [ 0 ]] != 0 ) { // curr_res has the total weight of the // solution we got int curr_res = curr_weight + adj [ curr_path [ level -1 ]][ curr_path [ 0 ]]; // Update final result and final path if // current result is better. if ( curr_res < final_res ) { copyToFinal ( curr_path ); final_res = curr_res ; } } return ; } // for any other level iterate for all vertices to // build the search space tree recursively for ( int i = 0 ; i < N ; i ++ ) { // Consider next vertex if it is not same (diagonal // entry in adjacency matrix and not visited // already) if ( adj [ curr_path [ level -1 ]][ i ] != 0 && visited [ i ] == false ) { int temp = curr_bound ; curr_weight += adj [ curr_path [ level -1 ]][ i ]; // different computation of curr_bound for // level 2 from the other levels if ( level == 1 ) curr_bound -= (( firstMin ( adj curr_path [ level -1 ]) + firstMin ( adj i )) / 2 ); else curr_bound -= (( secondMin ( adj curr_path [ level -1 ]) + firstMin ( adj i )) / 2 ); // curr_bound + curr_weight is the actual lower bound // for the node that we have arrived on // If current lower bound < final_res we need to explore // the node further if ( curr_bound + curr_weight < final_res ) { curr_path [ level ] = i ; visited [ i ] = true ; // call TSPRec for the next level TSPRec ( adj curr_bound curr_weight level + 1 curr_path ); } // Else we have to prune the node by resetting // all changes to curr_weight and curr_bound curr_weight -= adj [ curr_path [ level -1 ]][ i ]; curr_bound = temp ; // Also reset the visited array memset ( visited false sizeof ( visited )); for ( int j = 0 ; j <= level -1 ; j ++ ) visited [ curr_path [ j ]] = true ; } } } // This function sets up final_path[] void TSP ( int adj [ N ][ N ]) { int curr_path [ N + 1 ]; // Calculate initial lower bound for the root node // using the formula 1/2 * (sum of first min + // second min) for all edges. // Also initialize the curr_path and visited array int curr_bound = 0 ; memset ( curr_path -1 sizeof ( curr_path )); memset ( visited 0 sizeof ( curr_path )); // Compute initial bound for ( int i = 0 ; i < N ; i ++ ) curr_bound += ( firstMin ( adj i ) + secondMin ( adj i )); // Rounding off the lower bound to an integer curr_bound = ( curr_bound & 1 ) ? curr_bound / 2 + 1 : curr_bound / 2 ; // We start at vertex 1 so the first vertex // in curr_path[] is 0 visited [ 0 ] = true ; curr_path [ 0 ] = 0 ; // Call to TSPRec for curr_weight equal to // 0 and level 1 TSPRec ( adj curr_bound 0 1 curr_path ); } // Driver code int main () { //Adjacency matrix for the given graph int adj [ N ][ N ] = { { 0 10 15 20 } { 10 0 35 25 } { 15 35 0 30 } { 20 25 30 0 } }; TSP ( adj ); printf ( 'Minimum cost : %d n ' final_res ); printf ( 'Path Taken : ' ); for ( int i = 0 ; i <= N ; i ++ ) printf ( '%d ' final_path [ i ]); return 0 ; }
Java // Java program to solve Traveling Salesman Problem // using Branch and Bound. import java.util.* ; class GFG { static int N = 4 ; // final_path[] stores the final solution ie the // path of the salesman. static int final_path [] = new int [ N + 1 ] ; // visited[] keeps track of the already visited nodes // in a particular path static boolean visited [] = new boolean [ N ] ; // Stores the final minimum weight of shortest tour. static int final_res = Integer . MAX_VALUE ; // Function to copy temporary solution to // the final solution static void copyToFinal ( int curr_path [] ) { for ( int i = 0 ; i < N ; i ++ ) final_path [ i ] = curr_path [ i ] ; final_path [ N ] = curr_path [ 0 ] ; } // Function to find the minimum edge cost // having an end at the vertex i static int firstMin ( int adj [][] int i ) { int min = Integer . MAX_VALUE ; for ( int k = 0 ; k < N ; k ++ ) if ( adj [ i ][ k ] < min && i != k ) min = adj [ i ][ k ] ; return min ; } // function to find the second minimum edge cost // having an end at the vertex i static int secondMin ( int adj [][] int i ) { int first = Integer . MAX_VALUE second = Integer . MAX_VALUE ; for ( int j = 0 ; j < N ; j ++ ) { if ( i == j ) continue ; if ( adj [ i ][ j ] <= first ) { second = first ; first = adj [ i ][ j ] ; } else if ( adj [ i ][ j ] <= second && adj [ i ][ j ] != first ) second = adj [ i ][ j ] ; } return second ; } // function that takes as arguments: // curr_bound -> lower bound of the root node // curr_weight-> stores the weight of the path so far // level-> current level while moving in the search // space tree // curr_path[] -> where the solution is being stored which // would later be copied to final_path[] static void TSPRec ( int adj [][] int curr_bound int curr_weight int level int curr_path [] ) { // base case is when we have reached level N which // means we have covered all the nodes once if ( level == N ) { // check if there is an edge from last vertex in // path back to the first vertex if ( adj [ curr_path [ level - 1 ]][ curr_path [ 0 ]] != 0 ) { // curr_res has the total weight of the // solution we got int curr_res = curr_weight + adj [ curr_path [ level - 1 ]][ curr_path [ 0 ]] ; // Update final result and final path if // current result is better. if ( curr_res < final_res ) { copyToFinal ( curr_path ); final_res = curr_res ; } } return ; } // for any other level iterate for all vertices to // build the search space tree recursively for ( int i = 0 ; i < N ; i ++ ) { // Consider next vertex if it is not same (diagonal // entry in adjacency matrix and not visited // already) if ( adj [ curr_path [ level - 1 ]][ i ] != 0 && visited [ i ] == false ) { int temp = curr_bound ; curr_weight += adj [ curr_path [ level - 1 ]][ i ] ; // different computation of curr_bound for // level 2 from the other levels if ( level == 1 ) curr_bound -= (( firstMin ( adj curr_path [ level - 1 ] ) + firstMin ( adj i )) / 2 ); else curr_bound -= (( secondMin ( adj curr_path [ level - 1 ] ) + firstMin ( adj i )) / 2 ); // curr_bound + curr_weight is the actual lower bound // for the node that we have arrived on // If current lower bound < final_res we need to explore // the node further if ( curr_bound + curr_weight < final_res ) { curr_path [ level ] = i ; visited [ i ] = true ; // call TSPRec for the next level TSPRec ( adj curr_bound curr_weight level + 1 curr_path ); } // Else we have to prune the node by resetting // all changes to curr_weight and curr_bound curr_weight -= adj [ curr_path [ level - 1 ]][ i ] ; curr_bound = temp ; // Also reset the visited array Arrays . fill ( visited false ); for ( int j = 0 ; j <= level - 1 ; j ++ ) visited [ curr_path [ j ]] = true ; } } } // This function sets up final_path[] static void TSP ( int adj [][] ) { int curr_path [] = new int [ N + 1 ] ; // Calculate initial lower bound for the root node // using the formula 1/2 * (sum of first min + // second min) for all edges. // Also initialize the curr_path and visited array int curr_bound = 0 ; Arrays . fill ( curr_path - 1 ); Arrays . fill ( visited false ); // Compute initial bound for ( int i = 0 ; i < N ; i ++ ) curr_bound += ( firstMin ( adj i ) + secondMin ( adj i )); // Rounding off the lower bound to an integer curr_bound = ( curr_bound == 1 ) ? curr_bound / 2 + 1 : curr_bound / 2 ; // We start at vertex 1 so the first vertex // in curr_path[] is 0 visited [ 0 ] = true ; curr_path [ 0 ] = 0 ; // Call to TSPRec for curr_weight equal to // 0 and level 1 TSPRec ( adj curr_bound 0 1 curr_path ); } // Driver code public static void main ( String [] args ) { //Adjacency matrix for the given graph int adj [][] = {{ 0 10 15 20 } { 10 0 35 25 } { 15 35 0 30 } { 20 25 30 0 } }; TSP ( adj ); System . out . printf ( 'Minimum cost : %dn' final_res ); System . out . printf ( 'Path Taken : ' ); for ( int i = 0 ; i <= N ; i ++ ) { System . out . printf ( '%d ' final_path [ i ] ); } } } /* This code contributed by PrinciRaj1992 */
Python3 # Python3 program to solve # Traveling Salesman Problem using # Branch and Bound. import math maxsize = float ( 'inf' ) # Function to copy temporary solution # to the final solution def copyToFinal ( curr_path ): final_path [: N + 1 ] = curr_path [:] final_path [ N ] = curr_path [ 0 ] # Function to find the minimum edge cost # having an end at the vertex i def firstMin ( adj i ): min = maxsize for k in range ( N ): if adj [ i ][ k ] < min and i != k : min = adj [ i ][ k ] return min # function to find the second minimum edge # cost having an end at the vertex i def secondMin ( adj i ): first second = maxsize maxsize for j in range ( N ): if i == j : continue if adj [ i ][ j ] <= first : second = first first = adj [ i ][ j ] elif ( adj [ i ][ j ] <= second and adj [ i ][ j ] != first ): second = adj [ i ][ j ] return second # function that takes as arguments: # curr_bound -> lower bound of the root node # curr_weight-> stores the weight of the path so far # level-> current level while moving # in the search space tree # curr_path[] -> where the solution is being stored # which would later be copied to final_path[] def TSPRec ( adj curr_bound curr_weight level curr_path visited ): global final_res # base case is when we have reached level N # which means we have covered all the nodes once if level == N : # check if there is an edge from # last vertex in path back to the first vertex if adj [ curr_path [ level - 1 ]][ curr_path [ 0 ]] != 0 : # curr_res has the total weight # of the solution we got curr_res = curr_weight + adj [ curr_path [ level - 1 ]] [ curr_path [ 0 ]] if curr_res < final_res : copyToFinal ( curr_path ) final_res = curr_res return # for any other level iterate for all vertices # to build the search space tree recursively for i in range ( N ): # Consider next vertex if it is not same # (diagonal entry in adjacency matrix and # not visited already) if ( adj [ curr_path [ level - 1 ]][ i ] != 0 and visited [ i ] == False ): temp = curr_bound curr_weight += adj [ curr_path [ level - 1 ]][ i ] # different computation of curr_bound # for level 2 from the other levels if level == 1 : curr_bound -= (( firstMin ( adj curr_path [ level - 1 ]) + firstMin ( adj i )) / 2 ) else : curr_bound -= (( secondMin ( adj curr_path [ level - 1 ]) + firstMin ( adj i )) / 2 ) # curr_bound + curr_weight is the actual lower bound # for the node that we have arrived on. # If current lower bound < final_res # we need to explore the node further if curr_bound + curr_weight < final_res : curr_path [ level ] = i visited [ i ] = True # call TSPRec for the next level TSPRec ( adj curr_bound curr_weight level + 1 curr_path visited ) # Else we have to prune the node by resetting # all changes to curr_weight and curr_bound curr_weight -= adj [ curr_path [ level - 1 ]][ i ] curr_bound = temp # Also reset the visited array visited = [ False ] * len ( visited ) for j in range ( level ): if curr_path [ j ] != - 1 : visited [ curr_path [ j ]] = True # This function sets up final_path def TSP ( adj ): # Calculate initial lower bound for the root node # using the formula 1/2 * (sum of first min + # second min) for all edges. Also initialize the # curr_path and visited array curr_bound = 0 curr_path = [ - 1 ] * ( N + 1 ) visited = [ False ] * N # Compute initial bound for i in range ( N ): curr_bound += ( firstMin ( adj i ) + secondMin ( adj i )) # Rounding off the lower bound to an integer curr_bound = math . ceil ( curr_bound / 2 ) # We start at vertex 1 so the first vertex # in curr_path[] is 0 visited [ 0 ] = True curr_path [ 0 ] = 0 # Call to TSPRec for curr_weight # equal to 0 and level 1 TSPRec ( adj curr_bound 0 1 curr_path visited ) # Driver code # Adjacency matrix for the given graph adj = [[ 0 10 15 20 ] [ 10 0 35 25 ] [ 15 35 0 30 ] [ 20 25 30 0 ]] N = 4 # final_path[] stores the final solution # i.e. the // path of the salesman. final_path = [ None ] * ( N + 1 ) # visited[] keeps track of the already # visited nodes in a particular path visited = [ False ] * N # Stores the final minimum weight # of shortest tour. final_res = maxsize TSP ( adj ) print ( 'Minimum cost :' final_res ) print ( 'Path Taken : ' end = ' ' ) for i in range ( N + 1 ): print ( final_path [ i ] end = ' ' ) # This code is contributed by ng24_7
C# // C# program to solve Traveling Salesman Problem // using Branch and Bound. using System ; public class GFG { static int N = 4 ; // final_path[] stores the final solution ie the // path of the salesman. static int [] final_path = new int [ N + 1 ]; // visited[] keeps track of the already visited nodes // in a particular path static bool [] visited = new bool [ N ]; // Stores the final minimum weight of shortest tour. static int final_res = Int32 . MaxValue ; // Function to copy temporary solution to // the final solution static void copyToFinal ( int [] curr_path ) { for ( int i = 0 ; i < N ; i ++ ) final_path [ i ] = curr_path [ i ]; final_path [ N ] = curr_path [ 0 ]; } // Function to find the minimum edge cost // having an end at the vertex i static int firstMin ( int [ ] adj int i ) { int min = Int32 . MaxValue ; for ( int k = 0 ; k < N ; k ++ ) if ( adj [ i k ] < min && i != k ) min = adj [ i k ]; return min ; } // function to find the second minimum edge cost // having an end at the vertex i static int secondMin ( int [ ] adj int i ) { int first = Int32 . MaxValue second = Int32 . MaxValue ; for ( int j = 0 ; j < N ; j ++ ) { if ( i == j ) continue ; if ( adj [ i j ] <= first ) { second = first ; first = adj [ i j ]; } else if ( adj [ i j ] <= second && adj [ i j ] != first ) second = adj [ i j ]; } return second ; } // function that takes as arguments: // curr_bound -> lower bound of the root node // curr_weight-> stores the weight of the path so far // level-> current level while moving in the search // space tree // curr_path[] -> where the solution is being stored // which // would later be copied to final_path[] static void TSPRec ( int [ ] adj int curr_bound int curr_weight int level int [] curr_path ) { // base case is when we have reached level N which // means we have covered all the nodes once if ( level == N ) { // check if there is an edge from last vertex in // path back to the first vertex if ( adj [ curr_path [ level - 1 ] curr_path [ 0 ]] != 0 ) { // curr_res has the total weight of the // solution we got int curr_res = curr_weight + adj [ curr_path [ level - 1 ] curr_path [ 0 ]]; // Update final result and final path if // current result is better. if ( curr_res < final_res ) { copyToFinal ( curr_path ); final_res = curr_res ; } } return ; } // for any other level iterate for all vertices to // build the search space tree recursively for ( int i = 0 ; i < N ; i ++ ) { // Consider next vertex if it is not same // (diagonal entry in adjacency matrix and not // visited already) if ( adj [ curr_path [ level - 1 ] i ] != 0 && visited [ i ] == false ) { int temp = curr_bound ; curr_weight += adj [ curr_path [ level - 1 ] i ]; // different computation of curr_bound for // level 2 from the other levels if ( level == 1 ) curr_bound -= (( firstMin ( adj curr_path [ level - 1 ]) + firstMin ( adj i )) / 2 ); else curr_bound -= (( secondMin ( adj curr_path [ level - 1 ]) + firstMin ( adj i )) / 2 ); // curr_bound + curr_weight is the actual // lower bound for the node that we have // arrived on If current lower bound < // final_res we need to explore the node // further if ( curr_bound + curr_weight < final_res ) { curr_path [ level ] = i ; visited [ i ] = true ; // call TSPRec for the next level TSPRec ( adj curr_bound curr_weight level + 1 curr_path ); } // Else we have to prune the node by // resetting all changes to curr_weight and // curr_bound curr_weight -= adj [ curr_path [ level - 1 ] i ]; curr_bound = temp ; // Also reset the visited array Array . Fill ( visited false ); for ( int j = 0 ; j <= level - 1 ; j ++ ) visited [ curr_path [ j ]] = true ; } } } // This function sets up final_path[] static void TSP ( int [ ] adj ) { int [] curr_path = new int [ N + 1 ]; // Calculate initial lower bound for the root node // using the formula 1/2 * (sum of first min + // second min) for all edges. // Also initialize the curr_path and visited array int curr_bound = 0 ; Array . Fill ( curr_path - 1 ); Array . Fill ( visited false ); // Compute initial bound for ( int i = 0 ; i < N ; i ++ ) curr_bound += ( firstMin ( adj i ) + secondMin ( adj i )); // Rounding off the lower bound to an integer curr_bound = ( curr_bound == 1 ) ? curr_bound / 2 + 1 : curr_bound / 2 ; // We start at vertex 1 so the first vertex // in curr_path[] is 0 visited [ 0 ] = true ; curr_path [ 0 ] = 0 ; // Call to TSPRec for curr_weight equal to // 0 and level 1 TSPRec ( adj curr_bound 0 1 curr_path ); } // Driver code static public void Main () { // Adjacency matrix for the given graph int [ ] adj = { { 0 10 15 20 } { 10 0 35 25 } { 15 35 0 30 } { 20 25 30 0 } }; TSP ( adj ); Console . WriteLine ( 'Minimum cost : ' + final_res ); Console . Write ( 'Path Taken : ' ); for ( int i = 0 ; i <= N ; i ++ ) { Console . Write ( final_path [ i ] + ' ' ); } } } // This code is contributed by Rohit Pradhan
JavaScript const N = 4 ; // final_path[] stores the final solution ie the // path of the salesman. let final_path = Array ( N + 1 ). fill ( - 1 ); // visited[] keeps track of the already visited nodes // in a particular path let visited = Array ( N ). fill ( false ); // Stores the final minimum weight of shortest tour. let final_res = Number . MAX_SAFE_INTEGER ; // Function to copy temporary solution to // the final solution function copyToFinal ( curr_path ){ for ( let i = 0 ; i < N ; i ++ ){ final_path [ i ] = curr_path [ i ]; } final_path [ N ] = curr_path [ 0 ]; } // Function to find the minimum edge cost // having an end at the vertex i function firstMin ( adj i ){ let min = Number . MAX_SAFE_INTEGER ; for ( let k = 0 ; k < N ; k ++ ){ if ( adj [ i ][ k ] < min && i !== k ){ min = adj [ i ][ k ]; } } return min ; } // function to find the second minimum edge cost // having an end at the vertex i function secondMin ( adj i ){ let first = Number . MAX_SAFE_INTEGER ; let second = Number . MAX_SAFE_INTEGER ; for ( let j = 0 ; j < N ; j ++ ){ if ( i == j ){ continue ; } if ( adj [ i ][ j ] <= first ){ second = first ; first = adj [ i ][ j ]; } else if ( adj [ i ][ j ] <= second && adj [ i ][ j ] !== first ){ second = adj [ i ][ j ]; } } return second ; } // function that takes as arguments: // curr_bound -> lower bound of the root node // curr_weight-> stores the weight of the path so far // level-> current level while moving in the search // space tree // curr_path[] -> where the solution is being stored which // would later be copied to final_path[] function TSPRec ( adj curr_bound curr_weight level curr_path ) { // base case is when we have reached level N which // means we have covered all the nodes once if ( level == N ) { // check if there is an edge from last vertex in // path back to the first vertex if ( adj [ curr_path [ level - 1 ]][ curr_path [ 0 ]] !== 0 ) { // curr_res has the total weight of the // solution we got let curr_res = curr_weight + adj [ curr_path [ level - 1 ]][ curr_path [ 0 ]]; // Update final result and final path if // current result is better. if ( curr_res < final_res ) { copyToFinal ( curr_path ); final_res = curr_res ; } } return ; } // for any other level iterate for all vertices to // build the search space tree recursively for ( let i = 0 ; i < N ; i ++ ){ // Consider next vertex if it is not same (diagonal // entry in adjacency matrix and not visited // already) if ( adj [ curr_path [ level - 1 ]][ i ] !== 0 && ! visited [ i ]){ let temp = curr_bound ; curr_weight += adj [ curr_path [ level - 1 ]][ i ]; // different computation of curr_bound for // level 2 from the other levels if ( level == 1 ){ curr_bound -= ( firstMin ( adj curr_path [ level - 1 ]) + firstMin ( adj i )) / 2 ; } else { curr_bound -= ( secondMin ( adj curr_path [ level - 1 ]) + firstMin ( adj i )) / 2 ; } // curr_bound + curr_weight is the actual lower bound // for the node that we have arrived on // If current lower bound < final_res we need to explore // the node further if ( curr_bound + curr_weight < final_res ){ curr_path [ level ] = i ; visited [ i ] = true ; // call TSPRec for the next level TSPRec ( adj curr_bound curr_weight level + 1 curr_path ); } // Else we have to prune the node by resetting // all changes to curr_weight and curr_bound curr_weight -= adj [ curr_path [ level - 1 ]][ i ]; curr_bound = temp ; // Also reset the visited array visited . fill ( false ) for ( var j = 0 ; j <= level - 1 ; j ++ ) visited [ curr_path [ j ]] = true ; } } } // This function sets up final_path[] function TSP ( adj ) { let curr_path = Array ( N + 1 ). fill ( - 1 ); // Calculate initial lower bound for the root node // using the formula 1/2 * (sum of first min + // second min) for all edges. // Also initialize the curr_path and visited array let curr_bound = 0 ; visited . fill ( false ); // compute initial bound for ( let i = 0 ; i < N ; i ++ ){ curr_bound += firstMin ( adj i ) + secondMin ( adj i ); } // Rounding off the lower bound to an integer curr_bound = curr_bound == 1 ? ( curr_bound / 2 ) + 1 : ( curr_bound / 2 ); // We start at vertex 1 so the first vertex // in curr_path[] is 0 visited [ 0 ] = true ; curr_path [ 0 ] = 0 ; // Call to TSPRec for curr_weight equal to // 0 and level 1 TSPRec ( adj curr_bound 0 1 curr_path ); } //Adjacency matrix for the given graph let adj = [[ 0 10 15 20 ] [ 10 0 35 25 ] [ 15 35 0 30 ] [ 20 25 30 0 ]]; TSP ( adj ); console . log ( `Minimum cost: ${ final_res } ` ); console . log ( `Path Taken: ${ final_path . join ( ' ' ) } ` ); // This code is contributed by anskalyan3.
Saída :
Minimum cost : 80 Path Taken : 0 1 3 2 0
O arredondamento está sendo feito nesta linha de código:
if (level==1) curr_bound -= ((firstMin(adj curr_path[level-1]) + firstMin(adj i))/2); else curr_bound -= ((secondMin(adj curr_path[level-1]) + firstMin(adj i))/2);
No algoritmo TSP de ramificação e limite, calculamos um limite inferior ao custo total da solução ideal, adicionando os custos mínimos de borda para cada vértice e depois dividindo por dois. No entanto, esse limite inferior pode não ser um número inteiro. Para obter um limite inferior inteiro, podemos usar arredondamento.
No código acima, a variável curr_bound mantém o limite inferior atual no custo total da solução ideal. Quando visitamos um novo vértice no nível de nível, calculamos um novo candidato a limite inferior, obtendo a soma dos custos mínimos da borda para o novo vértice e seus dois vizinhos mais próximos. Em seguida, atualizamos a variável curr_bound arredondando new_bound para o número inteiro mais próximo.
Se o nível for 1, arredondamos até o número inteiro mais próximo. Isso ocorre porque já visitamos apenas um vértice e queremos ser conservadores em nossa estimativa do custo total da solução ideal. Se o nível for maior que 1, usamos uma estratégia de arredondamento mais agressiva que leva em consideração o fato de que já visitamos alguns vértices e, portanto, podemos fazer uma estimativa mais precisa do custo total da solução ideal.
Complexidade do tempo: A complexidade do pior caso de ramificação e limite permanece a mesma que a força bruta claramente, porque, na pior das hipóteses, podemos nunca ter a chance de podar um nó. Considerando que, na prática, ele tem um desempenho muito bom, dependendo da instância diferente da TSP. A complexidade também depende da escolha da função delimitadora, pois são os que decidem quantos nós são podados.
Referências:
http://lcm.csa.iisc.ernet.in/dsa/node187.html