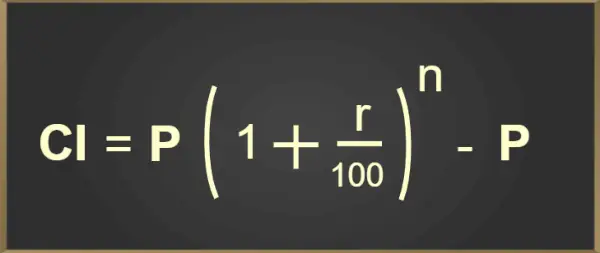
Odsetki składane to odsetki naliczane od kwoty pożyczki lub depozytu, w ramach których naliczane są odsetki od kwoty głównej oraz wcześniej naliczonych odsetek.

Wspólna różnica między odsetkami składanymi i prostymi polega na tym, że w odsetki składane odsetki naliczane są zarówno od kwoty kapitału, jak i od odsetek naliczonych wcześniej, natomiast odsetki proste zależą wyłącznie od zainwestowanego kapitału.

Spis treści

• Co to jest procent składany?
• Formuła odsetek składanych
• Jak obliczyć odsetki składane?
• Wzór na procent składany – wyprowadzenie
• Formuła półrocznego procentu składanego
• Kwartalna formuła odsetek składanych
• Formuła miesięcznego procentu składanego
• Dzienna formuła odsetek składanych
• Wzór na okresową stopę łączenia
• Zasada 72
• Odsetki składane za kolejne lata
• Formuła odsetek ciągłych składanych
• Niektóre inne zastosowania odsetek składanych
• Różnica między odsetkiem składanym a odsetkiem prostym
• Przykłady odsetek składanych
• Procent składany – pytania praktyczne

Co to jest procent składany?

Odsetki składane to odsetki od kwoty głównej oraz odsetki naliczone od kwoty głównej. Słowo procent składany składa się z dwóch słów Związek, który oznacza złożony z dwóch lub więcej, a Odsetki oznaczają pieniądze zarobione na pożyczeniu kwoty. Zatem odsetki składane to pieniądze zarobione na pożyczkach i składają się z dwóch rodzajów odsetek, którymi są:

• Odsetki od kwoty głównej

• Odsetki od odsetek naliczonych od kwoty głównej w danym okresie

Definicja odsetek składanych

Odsetki składane to odsetki naliczone od kwoty głównej i odsetek uzyskanych wcześniej. Jest to oznaczone przez C.I. Jest bardzo przydatny do celów inwestycyjnych i spłaty kredytów. Nazywa się je również odsetkami od odsetek.

Odsetki składane jest bardzo przydatny w sektorach bankowości i finansów, a także jest przydatny w innych sektorach. Oto kilka jego zastosowań:

• Wzrost liczby ludności kraju
• Wartość inwestycji w okresie czasu.
• Aby znaleźć zawyżone koszty i zamortyzowaną wartość dowolnego artykułu.
• Do przewidywania rozwoju dowolnej instytucji lub kraju.

Odsetki składane (C.I) = kwota – kwota główna

Formuła odsetek składanych

Procent składany oblicza się, po obliczeniu całkowitej kwoty w pewnym okresie, w oparciu o stopę procentową i kwotę kapitału początkowego. Dla początkowej kwoty głównej P, rocznej stopy procentowej r, okresu t w latach, częstotliwości kapitalizacji odsetek w ciągu roku n, wzór na obliczenie CI jest następujący:

CI = P(1 + r/100) ^N - P

Powyższy wzór na obliczanie odsetek składanych dodano w poniższej formie obrazkowej:

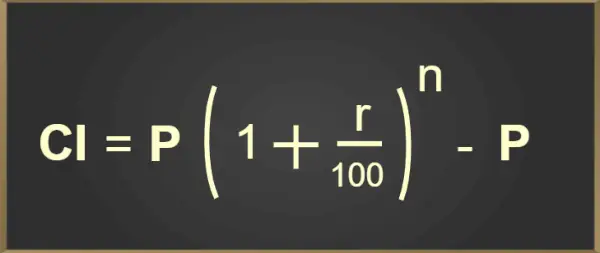
Formuła odsetek składanych

Gdzie,

• P = główny
• r = stopa procentowa
• n = Liczba naliczanych odsetek w ciągu roku
• t = czas (w latach)

Wzór na odsetki składane możemy zapisać jako:

Procent składany = A – P

Gdzie,

• A = Całkowita kwota pieniędzy po złożeniu
• P = Początkowa kwota główna

Procent składany = P(1 + r/n) ^nie -P

Gdzie,

• P = Początkowa kwota główna
• r = Roczna stopa procentowa
• n = liczba składanych odsetek
• t = liczba lat

Odsetki składane można obliczać rocznie, półrocznie, kwartalnie, miesięcznie, codziennie itp. zgodnie z wymaganiami.

Jak obliczyć odsetki składane?

Odsetki składane to odsetki płacone zarówno od kwoty głównej, jak i odsetek narosłych. Odsetki uzyskane w każdym przedziale czasu są dodawane do początkowej kwoty głównej, w ten sposób kwota główna rośnie.

Aby znaleźć odsetki składane, użyj następujących metod.

Krok 1: Podana uwaga, kwota główna, stawka i okres czasu

Krok 2: Oblicz kwotę korzystając ze wzoru A = P(1 + r/100) ^N

Krok 3: Znajdź odsetki składane, korzystając ze wzoru CI = kwota – kapitał

W regularnych odstępach czasu naliczone dotychczas odsetki są łączone z istniejącą kwotą główną, a następnie naliczane są odsetki obliczone dla nowego zleceniodawcy . Nowy kapitał jest równy sumie kapitału początkowego i dotychczas naliczonych odsetek.

Odsetki składane = odsetki od kwoty głównej + odsetki od odsetek od kwoty głównej (od drugiego roku i starsze)

Odsetki składane naliczane są w regularnych odstępach czasu, np. rocznie (rocznie), półrocznie, kwartalnie, miesięcznie, itp; To tak, jakby ponowne inwestowanie dochodów odsetkowych z inwestycji sprawiało, że pieniądze rosły szybciej w miarę upływu czasu! To jest dokładnie to, co procent składany robi z pieniędzmi. Banki lub jakakolwiek organizacja finansowa obliczają tę kwotę wyłącznie na podstawie odsetek składanych.

Wzór na procent składany – wyprowadzenie

Formuła odsetek składanych to potężne narzędzie stosowane w finansach do obliczania odsetek naliczonych lub zapłaconych od początkowej kwoty głównej, która obejmuje zarówno początkową kwotę główną, jak i odsetki narosłe w poprzednich okresach. Wzór na odsetki składane wyraża się wzorem:

Gdzie,

• A to przyszła wartość inwestycji lub pożyczki, łącznie z odsetkami
• P to kwota główna (początkowa kwota inwestycji lub pożyczki)
• r to roczna stopa procentowa (w postaci dziesiętnej)
• n oznacza liczbę kapitalizacji odsetek w ciągu roku
• t to czas Pieniądze są inwestowane lub pożyczane w latach

Prosta formuła odsetek

Odsetki proste naliczane są wyłącznie od kwoty głównej. Można to przedstawić za pomocą wzoru ,

Formuła odsetek składanych z ciągłym składaniem

W przypadku kapitalizacji odsetek w sposób ciągły (nieskończenie wiele razy w roku) wzór na odsetki składane wyprowadza się ze wzoru na kapitalizację ciągłą:

Gdzie,

• e jest liczbą Eulera (w przybliżeniu 2,71828)
• P to kwota główna
• r to roczna stopa procentowa
• t to czas w latach

Ogólny wzór na procent składany

Aby wyprowadzić ogólny wzór na odsetki składane, rozważmy składanie odsetek n razy w roku.

Jeśli P jest kapitalizowane n razy w roku według rocznej stopy procentowej r, odsetki r są dzielone przez n i stosowane n razy w roku. Zatem po t latach formuła wygląda następująco:

Gdzie,

• reprezentuje stopę procentową za okres kapitalizacji.
• nt to całkowita liczba okresów kumulacji w ciągu t lat.

Ten wzór ilustruje, jak początkowa kwota kapitału rośnie w czasie, gdy odsetki są kapitalizowane w regularnych odstępach czasu . Gdy n zbliża się do nieskończoności (tj. ciągłe składanie), wzór zbiega się w stronę wzoru na ciągłe składanie .

W podsumowaniu, wzór na procent składany jest wynikiem wzoru ciągłego łączenia dostosowanego do dyskretnych okresów łączenia w ciągu roku. Pozwala na wyliczenie przyszłej wartości inwestycji lub kredytu, uwzględniając w regularnych odstępach czasu odsetki składane.

Formuła półrocznego procentu składanego

Niech zainwestowana kwota kapitału wynosi P, a stopa procentowa wynosi R% rocznie i jest kapitalizowana co pół roku przez lata „t”

Jak jest kapitalizowany półrocznie, zmiana kapitału nastąpi po upływie 6 miesięcy, a odsetki zarobione do tego czasu zostaną dodane do kwoty głównej, a następnie stanie się ona nową kwotą główną. W podobny sposób obliczana jest ostateczna kwota.

Wiemy,

stawka = R% rocznie, składana co pół roku

stawka = (R/2)%

czas to t lat, wiemy, że ma t lat 2t pół roku.

Teraz,

A = P (1 + R/200) ^2t

CI = A – P

Kwartalna formuła odsetek składanych

Niech zainwestowana kwota kapitału wynosi P, a stopa procentowa wynosi R% rocznie i jest kapitalizowana kwartalnie przez t lat.

Jak jest kapitalizowany kwartalnie, zmiana kapitału nastąpi po upływie 3 miesięcy, I odsetki zarobione do tego czasu zostaną dodane do kwoty głównej, a następnie stanie się ona nową kwotą główną. W podobny sposób obliczana jest ostateczna kwota.

wiemy,

stopa = R% rocznie, kapitalizowana kwartalnie

stawka = (R/4)%

czas to t lat, wiemy, że ma t lat 4t mieszkanie.

Teraz,

A = P(1 + R/400) ^4t

CI = A – P

Sprawdzać: Kwartalna formuła odsetek składanych

Formuła miesięcznego procentu składanego

Jeśli odsetki są kapitalizowane co miesiąc, wówczas liczba składanych odsetek wyniesie 12, a odsetki w każdym miesiącu będą wynosić 1/12 rocznych odsetek składanych. W związku z tym miesięczny wzór odsetek składanych jest podany jako

A = P[1 + (R/1200)] ^12t

CI = A – P

Sprawdzać: Formuła miesięcznego procentu składanego

Dzienna formuła odsetek składanych

Jeśli odsetki są naliczane codziennie, to tak.

Nowa stopa procentowa wyniesie R/365%

n = 365

Stąd dzienny wzór na odsetki składane podaje się jako:

A = P[1 + (R/36500)] ^365t

CI = A – P

Wzór na okresową stopę łączenia

Kwotę całkowitą obejmującą kapitał P i odsetki składane CI wyraża się wzorem:

A = P[1 + (r/n)] ^nie

Gdzie,

• P = główny
• A = kwota ostateczna
• r = Roczna stopa procentowa
• n = liczba przypadków łączenia odsetek
• t = czas (w latach)

Zatem odsetki składane wynoszą:

CI = A – P

Zasada 72

Reguła 72 to wzór używany do oszacowania, przez ile lat nasze pieniądze zostaną podwojone, jeśli są składane co roku. Dla przykład , jeśli nasze pieniądze są inwestowane w R % składane corocznie, to potrzeba 72 lat, aby nasze pieniądze się podwoiły.

Kalkulacja ta jest również przydatna do obliczenia zawyżonej wartości naszych pieniędzy, tj. podaje, za ile lat wartość naszego aktywa zmniejszy się o połowę, jeśli będzie on corocznie amortyzowany.

Zasada 72 formuły

Poniższy wzór służy do przybliżenia liczby lat, po których nasza inwestycja ulegnie podwojeniu.

N = 72 / r

Gdzie,

• N to przybliżona liczba lat, w których nasze pieniądze zostają podwojone
• R to stopa, według której nasze pieniądze są łączone rocznie

Przykład Reguły 72

Załóżmy, że Kabir zainwestował 10 00 000 rupii w fundusz dłużny, który daje zwrot w wysokości 8%. Oblicz, po ilu latach suma pieniędzy ulegnie podwojeniu, jeśli będzie składana corocznie.

Korzystając z powyższego wzoru: N = 72/8 = 9 lat

Zatem, podwojenie pieniędzy Kabira zajmuje 9 lat.

Odsetki składane za kolejne lata

Jeśli mamy tę samą sumę i tę samą stopę procentową. CI danego roku jest zawsze większa niż CI z poprzedniego roku. (CI trzeciego roku jest większy niż CI drugiego roku). Różnica między CI za dowolne dwa kolejne lata to odsetki za jeden rok od CI z poprzedniego roku.

CI trzeciego roku – CI drugiego roku = CI drugiego roku × r × 1/100

Różnica pomiędzy kwotami z dwóch kolejnych lat stanowi odsetki za jeden rok od kwoty z roku poprzedniego.

Kwota z 3. roku – Kwota z 2. roku = Kwota z 2. roku × r × 1/100

Kluczowe wyniki

Gdy mamy tę samą sumę i tę samą stawkę ,

C.I za n-ty rok = CI za (n – 1) rok + odsetki za jeden rok od C.I za (n – 1) rok

Formuła odsetek ciągłych składanych

Formuła ciągłego łączenia jest stosowana w finansach do obliczania końcowej wartości inwestycji, która podlega ciągłemu składaniu w różnych okresach, a wartość jest dodawana w miarę upływu czasu. Wzór na ciągłe składanie podano jako

Wartość końcowa = wartość bieżąca × e ^rt

Gdzie,

• r to stopa procentowa
• czas

Ucz się więcej, Formuła ciągłego łączenia

Niektóre inne zastosowania odsetek składanych

Wzrost: Jest to wykorzystywane głównie do wzrostu, jeśli branże są powiązane.

Produkcja po n latach = produkcja początkowa × (1 + r/100) ^N

Amortyzacja: Jeżeli koszt produktu zmniejsza się o r% rocznie, wówczas jego wartość po n latach wynosi

Wartość bieżąca × (1 + r/100) ^N

Problemy populacyjne: Kiedy populacja miasta, miasteczka lub wsi rośnie w określonym tempie rocznie.

Populacja po n latach = obecna populacja × (1 + r/100) ^N

Różnica między odsetkiem składanym a odsetkiem prostym

Różnicę między odsetkiem złożonym a odsetkiem prostym można poznać poniżej w tym artykule

Odsetki składane a odsetki proste
Procent składany (CI)	Proste odsetki (SI)
CI to odsetki naliczane zarówno od kwoty głównej, jak i od wcześniej naliczonych odsetek.	SI to odsetki naliczane wyłącznie od kwoty głównej.
Na tej samej zasadzie, stawka i okres czasu CI> TAK	Na tej samej zasadzie, stawka i okres czasu TAK
Wzór na CI to A = P(1 + R/100) T CI = A – P	Wzór na SI to JEŻELI = (P×R×T) / 100

Przykłady odsetek składanych

Oto kilka przykładów wzorów na odsetki składane:

Przykład 1: Znajdź odsetki składane, gdy kapitał = 6000 Rs, stopa = 10% rocznie i czas = 2 lata.

Rozwiązanie:

Odsetki za pierwszy rok = (6000 × 10 × 1)/100 = 600

Kwota na koniec pierwszego roku = 6000 + 600 = 6600

Odsetki za drugi rok = (6600 × 10 × 1) / 100 = 660

Kwota na koniec drugiego roku = 6600 + 660 = 7260

Procent składany = 7260 – 6000 = 1260

Przykład 2: Jakie będą odsetki składane od 8000 rupii za dwa lata, gdy stopa procentowa wyniesie 2% rocznie?

Rozwiązanie:

Dany,

• Główny P = 8000
• Stawka r = 2%
• Czas = 2 lata

według formuły

A = P (1 + R/100) ^N

A = 8000 (1 + 2/100) ² = 8000 (102/100) ²

A = 8323

Odsetki składane = A – P = 8323 – 8000 = 323 Rs

Przykład 3: Hari zdeponował Rs. 4000 w firmie finansowej na 2 lata z oprocentowaniem 5% rocznie. Jakie odsetki składane otrzymuje Rohit po 2 latach?

Rozwiązanie:

Dany,

• Główny P = 4000
• Stawka r = 5%
• Czas = 2 lata

Według wzoru,

A = P (1 + R/100) ^N

A= 4000 (1 + 5/100) ²

A= 4000 (105/100) ²

A= 4410

Procent składany = A – P = 4410 – 4000 = 410

Przykład 4: Znajdź odsetki składane od Rs. 2000 r. w wysokości 4% rocznie przez 1,5 roku. Kiedy odsetki kapitalizowane są co pół roku?

Rozwiązanie:

Dany,

• Główne p = 2000
• Stawka r = 4%
• Czas = 1,5 (tj. 3 pół roku)

według wzoru,

A = P (1 + R/200) ²ⁿ

A = 2000 (1 + 4/200) ³

A = 2000 (204/200) ³

A = 2122

Procent składany = A – P = 2122 – 2000 = 122

Przykład 5: Jakie są odsetki składane od 10000 na jeden rok według stopy 20% w skali roku, jeśli odsetki są kapitalizowane kwartalnie?

Rozwiązanie:

Dany,

• Główny P = 10000 Rs
• Stawka R = 12% (12/4 = 3% na kwartał)
• Czas = 1 rok (1 × 4 = 4 kwartały)

Według formuły,

A = P (1 + R/100) ^N

A = 10000 (1 + 3/100) ⁴

A = 10000 (103/100) ⁴

A = 11255

Procent składany = A – P = 11255 – 10000 = 1255

Przykład 6: Znajdź odsetki składane w wysokości 5% rocznie przez 2 lata od tej kwoty głównej, które za 2 lata będą oprocentowane w wysokości 5% rocznie, biorąc pod uwagę Rs. 400 jako zwykłe odsetki.

Rozwiązanie:

Dany,

• Odsetki proste JEŻELI = 400
• Stawka R = 5%
• Czas T = 2 lata

Według formuły,

Prosty odsetek = (P × T × R)/100

⇒ P = (SI × 100)/T × R

P = (400 × 100)/2 × 5 Stopa procentu składanego = 5%

P = 40000/10 = 4000 Rs

Czas = 2 lata

Według formuły,

A = P (1 + R/100)

A = 4000 (1 + 5/100)

A = 4410

Procent składany = A – P = 4410 – 4000 = 410

Przykład 7: Znajdź odsetki składane od 30 000 rupii przy stopie procentowej 7% kapitalizowanej co roku przez dwa lata.

Rozwiązanie:

• Główny P = 30000 Rs
• Stawka R = 7%
• Czas = 2 lata

Według wzoru,

A = P (1 + R/100) ^N

A = 30000 (1 + 7/100) ²

A = 30000 (107/100) ²

A = 34347

Procent składany = A – P = 34347 – 30000 = 4347

Powiązane lektury:

• Dzienne odsetki składane
• Miesięczne odsetki składane
• Rozwiązanie odsetek składanych klasy 8
• Procent składany – pytania i odpowiedzi dotyczące umiejętności
• Proste zainteresowanie

Procent składany – pytania praktyczne

Różne pytania praktyczne dotyczące interesów składanych to:

Pytanie 1. Znajdź kwotę, którą należy spłacić po 3 latach, jeśli pożyczona zostanie suma 10000 przy stopie procentowej 4% kapitalizowanej rocznie.

Pytanie 2. Znajdź odsetki, które należy spłacić po 1,5 roku, jeśli pożyczono kwotę 2500 przy stopie procentowej 6% kapitalizowanej co pół roku.

Pytanie 3. Oblicz odsetki składane dla kwoty pożyczonej 9000 według stopy 5% kwartalnie przez 15 miesięcy.

Pytanie 4. Oblicz odsetki składane dla kwoty 20000 pożyczki według stopy 12% na 3 miesiące kapitalizowane miesięcznie

Wniosek dotyczący odsetek składanych

Odsetki składane to A potężna koncepcja finansowa, która pozwala na rozwój lub akumulację inwestycji lub pożyczek w czasie. w odróżnieniu odsetki proste, które naliczają odsetki wyłącznie od początkowej kwoty głównej, odsetki składane uwzględnia odsetki naliczone zarówno od początkowej kwoty głównej, jak i wszelkie skumulowane odsetki z poprzednich okresów.

Procent składany – często zadawane pytania

Co oznacza procent składany?

Odsetki składane to odsetki naliczane od kwoty głównej oraz odsetek poprzednich naliczonych w ustalonym okresie

Jak obliczyć odsetki składane?

Aby obliczyć odsetki składane, obliczana jest pierwsza ostateczna kwota, a następnie odejmuje się ją od kwoty głównej, aby uzyskać ostateczne odsetki składane. Kwotę oblicza się ze wzoru,

A = P(1 + R/100) ^T

CI = A – P

Czy dla inwestorów odsetki składane są lepsze niż odsetki proste?

Tak, odsetki składane są dla inwestorów znacznie lepsze niż odsetki proste.

Co to jest wzór na procent składany, jeśli jest kapitalizowany codziennie?

Załóżmy, że dana kwota główna wynosi P, stopa wynosi R, a przedział czasowy wynosi T lat, wówczas wzór na odsetki składane, gdy są kapitalizowane codziennie, wygląda następująco:

A = P(1 + R/365) ^{{365 × T}}

Jaka jest różnica między CI a SI?

Podstawowa różnica między CI i SI polega na tym, że SI to odsetki naliczane od kwoty głównej, podczas gdy CI to odsetki naliczane od kwoty głównej, a także odsetek narosłych od kwoty głównej