Jak znaleźć kąt w trójkącie prostokątnym?
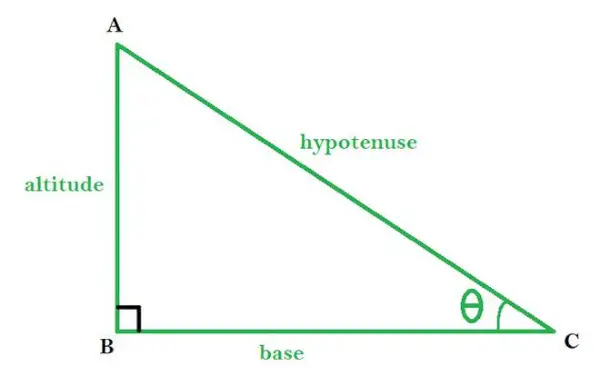
Trójkąty to trójboczne zamknięte wielokąty utworzone przez przecięcie trzech linii. Spotyka się go bardzo często w życiu codziennym. Jest to jedna z podstawowych kształtów geometrii. Ma trzy boki, trzy kąty i trzy wierzchołki. Trójkąt prostokątny to taki, w którym jeden z kątów jest zawsze równy 90°. Twierdzenie Pitagorasa wyprowadza się dla trójkątów prostokątnych, co stwierdza, że kwadrat przeciwprostokątnej (najdłuższego boku) jest równy sumie kwadratów podstawy i prostopadłej.
Mając długość co najmniej dwóch boków trójkąta prostokątnego, możemy znaleźć wartość dowolnego kąta w trójkącie prostokątnym. W tym celu używamy różnych funkcji trygonometrycznych, takich jak sinus, cosinus, tangens, cotangens, sec i cosec. Pomagają nam one powiązać kąty trójkąta prostokątnego z jego bokami.
Nieruchomości
- Pomiędzy trzema wierzchołkami znajduje się wierzchołek prostokątny
- Strona przeciwna do wierzchołka prostokątnego nazywa się przeciwprostokątna .
- Długość boków jest zgodna z twierdzeniem Pitagorasa, które stwierdza
przeciwprostokątna 2 = podstawa 2 + wysokość 2
- Przeciwprostokątna to najdłuższy bok trójkąta prostokątnego.
- Kąty inne niż kąt prosty są kątami ostrymi, ponieważ wartość jest mniejsza niż 90 O
Funkcje trygonometryczne

ABC jest trójkątem prostokątnym, w którym ∠B jest kątem prostym
- cosθ: Daje to stosunek podstawy do przeciwprostokątnej trójkąta prostokątnego.
cosθ = podstawa / przeciwprostokątna
- grzechθ: Daje to stosunek wysokości do przeciwprostokątnej trójkąta prostokątnego.
sinθ = wysokość / przeciwprostokątna
- tanθ: Jest to stosunek wysokości do podstawy trójkąta prostokątnego.
tanθ = wysokość / podstawa
- łóżeczkoθ: Jest to odwrotność tanθ
- sθ: Jest to odwrotność cosθ
- cosecθ: Jest to odwrotność sinθ
Aby znaleźć kąty trójkąta prostokątnego, możemy skorzystać z trygonometrycznej odwrotności stosunku danych boków trójkąta.
Przykład:
Jeżeli sinθ = x, to możemy pisać
θ = grzech -1 X.
Zwraca to kąt, dla którego wartość sinusowa kąta wynosi x.
Podobnie istnieje cos -1 θ, więc -1 ja, łóżeczko -1 θ, sek -1 θ i cosec -1 I
Przykładowe problemy
Pytanie 1. Dany jest trójkąt prostokątny o podstawie 10 cm i przeciwprostokątnej 20 cm. Znajdź wartość kąta bazowego.
Rozwiązanie:
Biorąc pod uwagę, podstawa = 10 cm
Przeciwprostokątna = 20 cm
Niech wartość kąta bazowego będzie wynosić θ. Możemy pisać
cosθ = podstawa / przeciwprostokątna = 10/20 = 1/2
θ = sałata -1 (1/2) = 60 O
Zatem wartość kąta bazowego wynosi 60 O .
Pytanie 2. Znajdź wartość kątów trójkąta prostokątnego, biorąc pod uwagę, że jeden z kątów ostrych jest dwa razy większy od drugiego.
Rozwiązanie:
Ponieważ wiemy, że suma wszystkich trzech kątów w trójkącie wynosi 180 O .
Ponieważ jeden z kątów ma miarę 90 O i jeden z kątów ostrych jest dwa razy większy od drugiego, możemy je uznać za θ i 2θ.
Zatem możemy pisać
90 O + θ + 2θ = 180 O
3θ = 180 O – 90 O
3θ = 90 O
θ = 90 O /3 = 30 O
2θ = 2 × 30 O = 60 O
Zatem kąty mają miarę 30 O , 60 O , i 90 O .
Zadanie 3. Znajdź wartość kąta wzniesienia drabiny o długości 5 m, wiedząc, że podstawa drabiny znajduje się w odległości 3 m od ściany.
Rozwiązanie:
Ponieważ drabina działa jak przeciwprostokątna trójkąta prostokątnego, a odległość od podstawy wynosi 3 m, możemy pisać
Przeciwprostokątna = 5m
Podstawa = 3m
Niech kąt wzniesienia będzie θ. Zatem możemy pisać
cosθ = podstawa / przeciwprostokątna = 3/5
θ = sałata -1 (3/5)
θ = 53 O
Zatem wartość kąta elewacji wynosi 53 O .
Zadanie 4. Znajdź wartość przeciwprostokątnej, wiedząc, że długość wysokości wynosi 8 m, a kąt przy podstawie wynosi 30 O .
Rozwiązanie:
Biorąc pod uwagę, że kąt bazowy jest równy 30 O a wysokość wynosi 8 m, możemy zastosować funkcję sinus, aby znaleźć długość przeciwprostokątnej.
grzech30 O = wysokość / przeciwprostokątna
przeciwprostokątna = wysokość / sin30 O
Ponieważ wartość sin30 O równa się 1/2, możemy zapisać
przeciwprostokątna = wysokość / (1/2) = 2 × wysokość
Zatem przeciwprostokątna = 2 × 8 = 16 m
Zatem długość przeciwprostokątnej jest równa 16m.