Sannsynlighet for at Knight forblir på sjakkbrettet


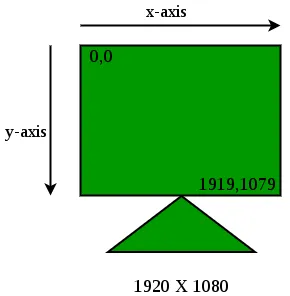
Gitt en n*n sjakkbrett og den ridder posisjon (x y) hver gang ridderen skal flytte, velger den ett av åtte mulige trekk jevnt kl tilfeldig (selv om brikken ville gå av sjakkbrettet) og beveger seg der. Ridderen fortsetter beveger seg til den har gjort nøyaktig k beveger seg eller har flyttet av sjakkbrettet. Oppgaven er å finne de sannsynlighet at ridderen rester på borde etter at den har stoppet flytte.
Note: En sjakkridder kan gjøre åtte mulige trekk. Hvert trekk er to celler i kardinalretning og deretter en celle i ortogonal retning.
Eksempler:
Inndata: n = 8 x = 0 y = 0 k = 1
Produksjon: 0,25
Forklaring: Ridderen starter på (0 0) og etter å ha tatt ett steg vil den ligge inne på brettet i bare 2 av 8 posisjoner som er (1 2) og (2 1). Dermed blir sannsynligheten 2/8 = 0,25.Inndata: n = 8 x = 0 y = 0 k = 3
Produksjon: 0,125Inndata: n = 4 x = 1 y = 2 k = 4
Produksjon: 0,024414
Innholdsfortegnelse
- Bruke Top-Down Dp (Memoisering) - O(n*n*k) Tid og O(n*n*k) Space
- Bruke Bottom-Up Dp (Tabulering) - O(n*n*k) Tid og O(n*n*k) Space
- Bruke romoptimalisert Dp - O(n*n*k) Tid og O(n*n) Mellomrom
Bruke Top-Down Dp (Memoisering) - O(n*n*k) Tid og O(n*n*k) Space
C++Sannsynligheten for at ridder forblir på sjakkbrettet etter k trekk er lik gjennomsnittet av sannsynligheten for ridder ved tidligere åtte posisjoner etter k - 1 trekk. På samme måte avhenger sannsynligheten etter k-1 trekk av gjennomsnittet av sannsynligheten etter k-2 trekk. Tanken er å bruke memoisering for å lagre sannsynlighetene for tidligere trekk og finne gjennomsnittet for å beregne det endelige resultatet.
For å gjøre det oppretter du en 3d array memo[][][] hvor memo[i][j][k] lagrer sannsynligheten for at ridder er i celle (i j) etter k trekk. Hvis k er null, dvs. starttilstanden er nådd retur 1 ellers utforske de åtte tidligere posisjonene og finn gjennomsnittet av sannsynlighetene deres.
// C++ program to find the probability of the // knight to remain inside the chessboard #include using namespace std ; // recursive function to calculate // knight probability double knightProbability ( int n int x int y int k vector < vector < vector < double >>> & memo ){ // Base case initial probability if ( k == 0 ) return 1.0 ; // check if already calculated if ( memo [ x ][ y ][ k ] != -1 ) return memo [ x ][ y ][ k ]; vector < vector < int >> directions = {{ 1 2 } { 2 1 } { 2 -1 } { 1 -2 } { -1 -2 } { -2 -1 } { -2 1 } { -1 2 }}; memo [ x ][ y ][ k ] = 0 ; double cur = 0.0 ; // for every position reachable from (xy) for ( auto d : directions ){ int u = x + d [ 0 ]; int v = y + d [ 1 ]; // if this position lie inside the board if ( u >= 0 && u < n && v >= 0 && v < n ) cur += knightProbability ( n u v k -1 memo ) / 8.0 ; } return memo [ x ][ y ][ k ] = cur ; } // Function to find the probability double findProb ( int n int x int y int k ) { // Initialize memo to store results vector < vector < vector < double >>> memo ( n vector < vector < double >> ( n vector < double > ( k + 1 -1 ))); return knightProbability ( n x y k memo ); } int main (){ int n = 8 x = 0 y = 0 k = 3 ; cout < < findProb ( n x y k ) < < endl ; return 0 ; }
Java // Java program to find the probability of the // knight to remain inside the chessboard class GfG { // recursive function to calculate // knight probability static double knightProbability ( int n int x int y int k double [][][] memo ) { // Base case initial probability if ( k == 0 ) return 1.0 ; // check if already calculated if ( memo [ x ][ y ][ k ] != - 1 ) return memo [ x ][ y ][ k ] ; int [][] directions = {{ 1 2 } { 2 1 } { 2 - 1 } { 1 - 2 } { - 1 - 2 } { - 2 - 1 } { - 2 1 } { - 1 2 }}; memo [ x ][ y ][ k ] = 0 ; double cur = 0.0 ; // for every position reachable from (x y) for ( int [] d : directions ) { int u = x + d [ 0 ] ; int v = y + d [ 1 ] ; // if this position lies inside the board if ( u >= 0 && u < n && v >= 0 && v < n ) cur += knightProbability ( n u v k - 1 memo ) / 8.0 ; } return memo [ x ][ y ][ k ] = cur ; } // Function to find the probability static double findProb ( int n int x int y int k ) { // Initialize memo to store results double [][][] memo = new double [ n ][ n ][ k + 1 ] ; for ( int i = 0 ; i < n ; i ++ ) { for ( int j = 0 ; j < n ; j ++ ) { for ( int m = 0 ; m <= k ; m ++ ) { memo [ i ][ j ][ m ] = - 1 ; } } } return knightProbability ( n x y k memo ); } public static void main ( String [] args ) { int n = 8 x = 0 y = 0 k = 3 ; System . out . println ( findProb ( n x y k )); } }
Python # Python program to find the probability of the # knight to remain inside the chessboard # recursive function to calculate # knight probability def knightProbability ( n x y k memo ): # Base case initial probability if k == 0 : return 1.0 # check if already calculated if memo [ x ][ y ][ k ] != - 1 : return memo [ x ][ y ][ k ] directions = [ [ 1 2 ] [ 2 1 ] [ 2 - 1 ] [ 1 - 2 ] [ - 1 - 2 ] [ - 2 - 1 ] [ - 2 1 ] [ - 1 2 ] ] memo [ x ][ y ][ k ] = 0 cur = 0.0 # for every position reachable from (x y) for d in directions : u = x + d [ 0 ] v = y + d [ 1 ] # if this position lies inside the board if 0 <= u < n and 0 <= v < n : cur += knightProbability ( n u v k - 1 memo ) / 8.0 memo [ x ][ y ][ k ] = cur return cur # Function to find the probability def findProb ( n x y k ): # Initialize memo to store results memo = [[[ - 1 for _ in range ( k + 1 )] for _ in range ( n )] for _ in range ( n )] return knightProbability ( n x y k memo ) n x y k = 8 0 0 3 print ( findProb ( n x y k ))
C# // C# program to find the probability of the // knight to remain inside the chessboard using System ; class GfG { // recursive function to calculate // knight probability static double KnightProbability ( int n int x int y int k double [] memo ) { // Base case initial probability if ( k == 0 ) return 1.0 ; // check if already calculated if ( memo [ x y k ] != - 1 ) return memo [ x y k ]; int [] directions = {{ 1 2 } { 2 1 } { 2 - 1 } { 1 - 2 } { - 1 - 2 } { - 2 - 1 } { - 2 1 } { - 1 2 }}; memo [ x y k ] = 0 ; double cur = 0.0 ; // for every position reachable from (x y) for ( int i = 0 ; i < 8 ; i ++ ) { int u = x + directions [ i 0 ]; int v = y + directions [ i 1 ]; // if this position lies inside the board if ( u >= 0 && u < n && v >= 0 && v < n ) { cur += KnightProbability ( n u v k - 1 memo ) / 8.0 ; } } return memo [ x y k ] = cur ; } // Function to find the probability static double FindProb ( int n int x int y int k ) { // Initialize memo to store results double [] memo = new double [ n n k + 1 ]; for ( int i = 0 ; i < n ; i ++ ) { for ( int j = 0 ; j < n ; j ++ ) { for ( int m = 0 ; m <= k ; m ++ ) { memo [ i j m ] = - 1 ; } } } return KnightProbability ( n x y k memo ); } static void Main () { int n = 8 x = 0 y = 0 k = 3 ; Console . WriteLine ( FindProb ( n x y k )); } }
JavaScript // JavaScript program to find the probability of the // knight to remain inside the chessboard // recursive function to calculate // knight probability function knightProbability ( n x y k memo ) { // Base case initial probability if ( k === 0 ) return 1.0 ; // check if already calculated if ( memo [ x ][ y ][ k ] !== - 1 ) return memo [ x ][ y ][ k ]; const directions = [ [ 1 2 ] [ 2 1 ] [ 2 - 1 ] [ 1 - 2 ] [ - 1 - 2 ] [ - 2 - 1 ] [ - 2 1 ] [ - 1 2 ] ]; memo [ x ][ y ][ k ] = 0 ; let cur = 0.0 ; // for every position reachable from (x y) for ( let d of directions ) { const u = x + d [ 0 ]; const v = y + d [ 1 ]; // if this position lies inside the board if ( u >= 0 && u < n && v >= 0 && v < n ) { cur += knightProbability ( n u v k - 1 memo ) / 8.0 ; } } return memo [ x ][ y ][ k ] = cur ; } // Function to find the probability function findProb ( n x y k ) { // Initialize memo to store results const memo = Array . from ({ length : n } () => Array . from ({ length : n } () => Array ( k + 1 ). fill ( - 1 ))); return knightProbability ( n x y k memo ). toFixed ( 6 ); } const n = 8 x = 0 y = 0 k = 3 ; console . log ( findProb ( n x y k ));
Produksjon
0.125
Bruke Bottom-Up Dp (Tabulering) - O(n*n*k) Tid og O(n*n*k) Space
C++Tilnærmingen ovenfor kan optimaliseres ved hjelp av nedenfra og opp tabulering som reduserer den ekstra plassen som kreves for rekursiv stabel. Tanken er å opprettholde en 3 D array dp[][][] hvor dp[i][j][k] lagrer sannsynligheten for at ridder er på cellen (i j) etter k beveger seg. Initialiser 0 tilstand av dp med verdi 1 . For hvert påfølgende trekk sannsynlighet av ridder vil være lik til gjennomsnittlig av sannsynlighet for tidligere 8 stillinger etter k-1 beveger seg.
// C++ program to find the probability of the // knight to remain inside the chessboard #include using namespace std ; // Function to find the probability double findProb ( int n int x int y int k ) { // Initialize dp to store results of each step vector < vector < vector < double >>> dp ( n vector < vector < double >> ( n vector < double > ( k + 1 ))); // Initialize dp for step 0 for ( int i = 0 ; i < n ; ++ i ) { for ( int j = 0 ; j < n ; ++ j ) { dp [ i ][ j ][ 0 ] = 1.0 ; } } vector < vector < int >> directions = { { 1 2 } { 2 1 } { 2 -1 } { 1 -2 } { -1 -2 } { -2 -1 } { -2 1 } { -1 2 } }; for ( int move = 1 ; move <= k ; move ++ ) { // find probability for cell (i j) for ( int i = 0 ; i < n ; ++ i ) { for ( int j = 0 ; j < n ; ++ j ) { double cur = 0.0 ; // for every position reachable from (xy) for ( auto d : directions ) { int u = i + d [ 0 ]; int v = j + d [ 1 ]; // if this position lie inside the board if ( u >= 0 && u < n && v >= 0 && v < n ) cur += dp [ u ][ v ][ move - 1 ] / 8.0 ; } // store the result dp [ i ][ j ][ move ] = cur ; } } } // return the result return dp [ x ][ y ][ k ]; } int main (){ int n = 8 x = 0 y = 0 k = 3 ; cout < < findProb ( n x y k ) < < endl ; return 0 ; }
Java // Java program to find the probability of the // knight to remain inside the chessboard import java.util.* ; class GfG { // Function to find the probability static double findProb ( int n int x int y int k ) { // Initialize dp to store results of each step double [][][] dp = new double [ n ][ n ][ k + 1 ] ; for ( int i = 0 ; i < n ; i ++ ) { for ( int j = 0 ; j < n ; j ++ ) { dp [ i ][ j ][ 0 ] = 1 ; } } int [][] directions = { { 1 2 } { 2 1 } { 2 - 1 } { 1 - 2 } { - 1 - 2 } { - 2 - 1 } { - 2 1 } { - 1 2 } }; for ( int move = 1 ; move <= k ; move ++ ) { // find probability for cell (i j) for ( int i = 0 ; i < n ; ++ i ) { for ( int j = 0 ; j < n ; ++ j ) { double cur = 0.0 ; // for every position reachable from (x y) for ( int [] d : directions ) { int u = i + d [ 0 ] ; int v = j + d [ 1 ] ; // if this position lies inside the board if ( u >= 0 && u < n && v >= 0 && v < n ) { cur += dp [ u ][ v ][ move - 1 ] / 8.0 ; } } // store the result dp [ i ][ j ][ move ] = cur ; } } } // return the result return dp [ x ][ y ][ k ] ; } public static void main ( String [] args ) { int n = 8 x = 0 y = 0 k = 3 ; System . out . println ( findProb ( n x y k )); } }
Python # Python program to find the probability of the # knight to remain inside the chessboard # Function to find the probability def findProb ( n x y k ): # Initialize dp to store results of each step dp = [[[ 0 for _ in range ( k + 1 )] for _ in range ( n )] for _ in range ( n )] for i in range ( n ): for j in range ( n ): dp [ i ][ j ][ 0 ] = 1.0 directions = [[ 1 2 ] [ 2 1 ] [ 2 - 1 ] [ 1 - 2 ] [ - 1 - 2 ] [ - 2 - 1 ] [ - 2 1 ] [ - 1 2 ]] for move in range ( 1 k + 1 ): # find probability for cell (i j) for i in range ( n ): for j in range ( n ): cur = 0.0 # for every position reachable from (x y) for d in directions : u = i + d [ 0 ] v = j + d [ 1 ] # if this position lies inside the board if 0 <= u < n and 0 <= v < n : cur += dp [ u ][ v ][ move - 1 ] / 8.0 # store the result dp [ i ][ j ][ move ] = cur # return the result return dp [ x ][ y ][ k ] if __name__ == '__main__' : n x y k = 8 0 0 3 print ( findProb ( n x y k ))
C# // C# program to find the probability of the // knight to remain inside the chessboard using System ; class GfG { // Function to find the probability static double findProb ( int n int x int y int k ) { // Initialize dp to store results of each step double [] dp = new double [ n n k + 1 ]; for ( int i = 0 ; i < n ; i ++ ) { for ( int j = 0 ; j < n ; j ++ ) { dp [ i j 0 ] = 1.0 ; } } int [] directions = {{ 1 2 } { 2 1 } { 2 - 1 } { 1 - 2 } { - 1 - 2 } { - 2 - 1 } { - 2 1 } { - 1 2 }}; for ( int move = 1 ; move <= k ; move ++ ) { // find probability for cell (i j) for ( int i = 0 ; i < n ; ++ i ) { for ( int j = 0 ; j < n ; ++ j ) { double cur = 0.0 ; // for every position reachable from (x y) for ( int d = 0 ; d < directions . GetLength ( 0 ); d ++ ) { int u = i + directions [ d 0 ]; int v = j + directions [ d 1 ]; // if this position lies inside the board if ( u >= 0 && u < n && v >= 0 && v < n ) { cur += dp [ u v move - 1 ] / 8.0 ; } } // store the result dp [ i j move ] = cur ; } } } // return the result return dp [ x y k ]; } static void Main ( string [] args ) { int n = 8 x = 0 y = 0 k = 3 ; Console . WriteLine ( findProb ( n x y k )); } }
JavaScript // JavaScript program to find the probability of the // knight to remain inside the chessboard // Function to find the probability function findProb ( n x y k ) { // Initialize dp to store results of each step let dp = Array . from ({ length : n } () => Array . from ({ length : n } () => Array ( k + 1 ). fill ( 0 )) ); // Initialize dp for step 0 for ( let i = 0 ; i < n ; ++ i ) { for ( let j = 0 ; j < n ; ++ j ) { dp [ i ][ j ][ 0 ] = 1.0 ; } } let directions = [[ 1 2 ] [ 2 1 ] [ 2 - 1 ] [ 1 - 2 ] [ - 1 - 2 ] [ - 2 - 1 ] [ - 2 1 ] [ - 1 2 ]]; for ( let move = 1 ; move <= k ; move ++ ) { // find probability for cell (i j) for ( let i = 0 ; i < n ; i ++ ) { for ( let j = 0 ; j < n ; j ++ ) { let cur = 0.0 ; // for every position reachable from (x y) for ( let d of directions ) { let u = i + d [ 0 ]; let v = j + d [ 1 ]; // if this position lies inside the board if ( u >= 0 && u < n && v >= 0 && v < n ) { cur += dp [ u ][ v ][ move - 1 ] / 8.0 ; } } // store the result dp [ i ][ j ][ move ] = cur ; } } } // return the result return dp [ x ][ y ][ k ]. toFixed ( 6 ); } let n = 8 x = 0 y = 0 k = 3 ; console . log ( findProb ( n x y k ));
Produksjon
0.125
Bruke romoptimalisert Dp - O(n*n*k) Tid og O(n*n) Mellomrom
C++Tilnærmingen ovenfor krever bare tidligere sannsynlighetstilstand for å beregne nåværende oppgi slik bare de tidligere butikken må lagres. Tanken er å lage to 2d-matriser prevMove[][] og currMove[][] hvor
- prevMove[i][j] lagrer sannsynligheten for at ridder er på (i j) opp til forrige trekk. Den initialiseres med verdi 1 for starttilstand.
- currMove[i][j] lagrer sannsynligheten for gjeldende tilstand.
Betjen på samme måte som tilnærmingen ovenfor og kl slutt av hver iterasjon update prevMove[][] med verdi lagret i currMove[][].
// C++ program to find the probability of the // knight to remain inside the chessboard #include using namespace std ; // Function to find the probability double findProb ( int n int x int y int k ) { // dp to store results of previous move vector < vector < double >> prevMove ( n vector < double > ( n 1 )); // dp to store results of current move vector < vector < double >> currMove ( n vector < double > ( n 0 )); vector < vector < int >> directions = { { 1 2 } { 2 1 } { 2 -1 } { 1 -2 } { -1 -2 } { -2 -1 } { -2 1 } { -1 2 } }; for ( int move = 1 ; move <= k ; move ++ ) { // find probability for cell (i j) for ( int i = 0 ; i < n ; ++ i ) { for ( int j = 0 ; j < n ; ++ j ) { double cur = 0.0 ; // for every position reachable from (xy) for ( auto d : directions ) { int u = i + d [ 0 ]; int v = j + d [ 1 ]; // if this position lie inside the board if ( u >= 0 && u < n && v >= 0 && v < n ) cur += prevMove [ u ][ v ] / 8.0 ; } // store the result currMove [ i ][ j ] = cur ; } } // update previous state prevMove = currMove ; } // return the result return prevMove [ x ][ y ]; } int main (){ int n = 8 x = 0 y = 0 k = 3 ; cout < < findProb ( n x y k ) < < endl ; return 0 ; }
Java // Java program to find the probability of the // knight to remain inside the chessboard class GfG { // Function to find the probability static double findProb ( int n int x int y int k ) { // dp to store results of previous move double [][] prevMove = new double [ n ][ n ] ; for ( int i = 0 ; i < n ; i ++ ) { for ( int j = 0 ; j < n ; j ++ ) { prevMove [ i ][ j ] = 1.0 ; } } // dp to store results of current move double [][] currMove = new double [ n ][ n ] ; int [][] directions = { { 1 2 } { 2 1 } { 2 - 1 } { 1 - 2 } { - 1 - 2 } { - 2 - 1 } { - 2 1 } { - 1 2 } }; for ( int move = 1 ; move <= k ; move ++ ) { // find probability for cell (i j) for ( int i = 0 ; i < n ; ++ i ) { for ( int j = 0 ; j < n ; ++ j ) { double cur = 0.0 ; // for every position reachable from (xy) for ( int [] d : directions ) { int u = i + d [ 0 ] ; int v = j + d [ 1 ] ; // if this position lies inside the board if ( u >= 0 && u < n && v >= 0 && v < n ) cur += prevMove [ u ][ v ] / 8.0 ; } // store the result currMove [ i ][ j ] = cur ; } } // update previous state for ( int i = 0 ; i < n ; i ++ ) { System . arraycopy ( currMove [ i ] 0 prevMove [ i ] 0 n ); } } // return the result return prevMove [ x ][ y ] ; } public static void main ( String [] args ) { int n = 8 x = 0 y = 0 k = 3 ; System . out . println ( findProb ( n x y k )); } }
Python # Python program to find the probability of the # knight to remain inside the chessboard def findProb ( n x y k ): # dp to store results of previous move prevMove = [[ 1.0 ] * n for _ in range ( n )] # dp to store results of current move currMove = [[ 0.0 ] * n for _ in range ( n )] directions = [ [ 1 2 ] [ 2 1 ] [ 2 - 1 ] [ 1 - 2 ] [ - 1 - 2 ] [ - 2 - 1 ] [ - 2 1 ] [ - 1 2 ] ] for move in range ( 1 k + 1 ): # find probability for cell (i j) for i in range ( n ): for j in range ( n ): cur = 0.0 # for every position reachable from (xy) for d in directions : u v = i + d [ 0 ] j + d [ 1 ] # if this position lies inside the board if 0 <= u < n and 0 <= v < n : cur += prevMove [ u ][ v ] / 8.0 # store the result currMove [ i ][ j ] = cur # update previous state prevMove = [ row [:] for row in currMove ] # return the result return prevMove [ x ][ y ] if __name__ == '__main__' : n x y k = 8 0 0 3 print ( findProb ( n x y k ))
C# // C# program to find the probability of the // knight to remain inside the chessboard using System ; class GfG { // Function to find the probability static double findProb ( int n int x int y int k ) { // dp to store results of previous move double [] prevMove = new double [ n n ]; for ( int i = 0 ; i < n ; i ++ ) for ( int j = 0 ; j < n ; j ++ ) prevMove [ i j ] = 1.0 ; // dp to store results of current move double [] currMove = new double [ n n ]; int [] directions = { { 1 2 } { 2 1 } { 2 - 1 } { 1 - 2 } { - 1 - 2 } { - 2 - 1 } { - 2 1 } { - 1 2 } }; for ( int move = 1 ; move <= k ; move ++ ) { // find probability for cell (i j) for ( int i = 0 ; i < n ; ++ i ) { for ( int j = 0 ; j < n ; ++ j ) { double cur = 0.0 ; // for every position reachable from (xy) for ( int d = 0 ; d < directions . GetLength ( 0 ); d ++ ) { int u = i + directions [ d 0 ]; int v = j + directions [ d 1 ]; // if this position lies inside the board if ( u >= 0 && u < n && v >= 0 && v < n ) cur += prevMove [ u v ] / 8.0 ; } // store the result currMove [ i j ] = cur ; } } // update previous state Array . Copy ( currMove prevMove n * n ); } // return the result return prevMove [ x y ]; } static void Main () { int n = 8 x = 0 y = 0 k = 3 ; Console . WriteLine ( findProb ( n x y k )); } }
JavaScript // JavaScript program to find the probability of the // knight to remain inside the chessboard function findProb ( n x y k ) { // dp to store results of previous move let prevMove = Array . from ({ length : n } () => Array ( n ). fill ( 1.0 )); // dp to store results of current move let currMove = Array . from ({ length : n } () => Array ( n ). fill ( 0.0 )); const directions = [ [ 1 2 ] [ 2 1 ] [ 2 - 1 ] [ 1 - 2 ] [ - 1 - 2 ] [ - 2 - 1 ] [ - 2 1 ] [ - 1 2 ] ]; for ( let move = 1 ; move <= k ; move ++ ) { // find probability for cell (i j) for ( let i = 0 ; i < n ; i ++ ) { for ( let j = 0 ; j < n ; j ++ ) { let cur = 0.0 ; // for every position reachable from (xy) for ( let d of directions ) { let u = i + d [ 0 ]; let v = j + d [ 1 ]; // if this position lies inside the board if ( u >= 0 && u < n && v >= 0 && v < n ) cur += prevMove [ u ][ v ] / 8.0 ; } // store the result currMove [ i ][ j ] = cur ; } } // update previous state prevMove = currMove . map ( row => [... row ]); } // return the result return prevMove [ x ][ y ]. toFixed ( 6 ); } let n = 8 x = 0 y = 0 k = 3 ; console . log ( findProb ( n x y k ));
Produksjon
0.125Lag quiz