Kombinasjonskretsen som endrer den binære informasjonen til 2 ^N utgangslinjer er kjent som Dekodere. Den binære informasjonen sendes i form av N inngangslinjer. Utgangslinjene definerer 2 ^N -bitkode for den binære informasjonen. Med enkle ord Dekoder utfører omvendt operasjon av Enkoder . Av gangen aktiveres kun én inngangslinje for enkelhets skyld. Den produserte 2 ^N -bit utgangskode tilsvarer den binære informasjonen.

Det finnes ulike typer dekodere som er som følger:

2 til 4 linjers dekoder:

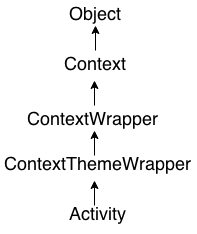
I 2 til 4 linjers dekoder er det totalt tre innganger, dvs. A ₀ , og A ₁ og E og fire utganger, dvs. Y ₀ , OG ₁ , OG ₂ , og Y ₃ . For hver kombinasjon av innganger, når aktiverings 'E' er satt til 1, vil en av disse fire utgangene være 1. Blokkdiagrammet og sannhetstabellen for 2 til 4 linjers dekoder er gitt nedenfor.

Blokkdiagram:

Sannhetstabell:

Det logiske uttrykket for begrepet Y0, Y0, Y2 og Y3 er som følger:

OG ₃ =E.A ₁ .EN ₀
OG ₂ =E.A ₁ .EN ₀ '
OG ₁ =E.A ₁ '.EN ₀
Y0=E.A ₁ '.EN ₀ '

Den logiske kretsen av uttrykkene ovenfor er gitt nedenfor:

3 til 8 linjers dekoder:

3 til 8 linjers dekoder er også kjent som Binær til oktal dekoder . I en 3 til 8 linjers dekoder er det totalt åtte utganger, dvs. Y ₀ , OG ₁ , OG ₂ , OG ₃ , OG ₄ , OG ₅ , OG ₆ , og Y ₇ og tre utganger, dvs. A ₀ , A1 og A ₂ . Denne kretsen har en aktiveringsinngang 'E'. Akkurat som 2 til 4 linjers dekoder, når aktiverings 'E' er satt til 1, vil en av disse fire utgangene være 1. Blokkdiagrammet og sannhetstabellen for 3 til 8 linjers koder er gitt nedenfor.

Blokkdiagram:

Sannhetstabell:

Det logiske uttrykket for begrepet Y ₀ , OG ₁ , OG ₂ , OG ₃ , OG ₄ , OG ₅ , OG ₆ , og Y ₇ er som følgende:

OG ₀ =A ₀ '.EN ₁ '.EN ₂ '
OG ₁ =A ₀ .EN ₁ '.EN ₂ '
OG ₂ =A ₀ '.EN ₁ .EN ₂ '
OG ₃ =A ₀ .EN ₁ .EN ₂ '
OG ₄ =A ₀ '.EN ₁ '.EN ₂
OG ₅ =A ₀ .EN ₁ '.EN ₂
OG ₆ =A ₀ '.EN ₁ .EN ₂
OG ₇ =A ₀ .EN ₁ .EN ₂

Den logiske kretsen av uttrykkene ovenfor er gitt nedenfor:

4 til 16 linjers dekoder

I dekoderen med 4 til 16 linjer er det totalt 16 utganger, dvs. Y ₀ , OG ₁ , OG ₂ ,……, OG ₁₆ og fire innganger, dvs. A ₀ , A1, A ₂ , og A ₃ . 3 til 16 linjers dekoder kan konstrueres med enten 2 til 4 dekoder eller 3 til 8 dekoder. Det er følgende formel som brukes for å finne det nødvendige antallet dekodere av lavere orden.

Nødvendig antall lavere ordens dekodere=m ₂ /m ₁

m ₁ = 8
m ₂ = 16

Nødvendig antall 3 til 8 dekodere= =2

Blokkdiagram:

Sannhetstabell:

Det logiske uttrykket for begrepet A0, A1, A2,..., A15 er som følger:

OG ₀ =A ₀ '.EN ₁ '.EN ₂ '.EN ₃ '
OG ₁ =A ₀ '.EN ₁ '.EN ₂ '.EN ₃
OG ₂ =A ₀ '.EN ₁ '.EN ₂ .EN ₃ '
OG ₃ =A ₀ '.EN ₁ '.EN ₂ .EN ₃
OG ₄ =A ₀ '.EN ₁ .EN ₂ '.EN ₃ '
OG ₅ =A ₀ '.EN ₁ .EN ₂ '.EN ₃
OG ₆ =A ₀ '.EN ₁ .EN ₂ .EN ₃ '
OG ₇ =A ₀ '.EN ₁ .EN ₂ .EN ₃
OG ₈ =A ₀ .EN ₁ '.EN ₂ '.EN ₃ '
OG ₉ =A ₀ .EN ₁ '.EN ₂ '.EN ₃
OG ₁₀ =A ₀ .EN ₁ '.EN ₂ .EN ₃ '
OG _elleve =A ₀ .EN ₁ '.EN ₂ .EN ₃
OG ₁₂ =A ₀ .EN ₁ .EN ₂ '.EN ₃ '
OG _{1. 3} =A ₀ .EN ₁ .EN ₂ '.EN ₃
OG ₁₄ =A ₀ .EN ₁ .EN ₂ .EN ₃ '
OG _femten =A ₀ .EN ₁ .EN ₂ '.EN ₃

Den logiske kretsen av uttrykkene ovenfor er gitt nedenfor: