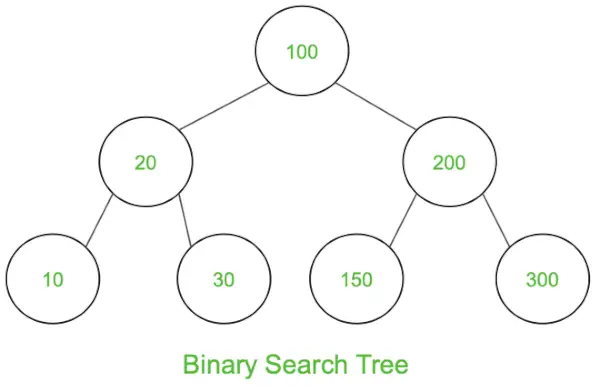
Zoek maximale lengte slangenreeks
Gegeven een raster van getallen, zoek maximale lengte slangenreeks en druk het af. Als er meerdere slangensequenties bestaan met de maximale lengte print een van deze.
Een slangenreeks bestaat uit aangrenzende getallen in het raster zodat voor elk nummer het nummer rechts of het onderstaande nummer +1 of -1 de waarde ervan is. Als u bijvoorbeeld op locatie (x y) in het raster bent, kunt u naar rechts gaan, d.w.z. (x y+1) als dat nummer ± 1 is of naar beneden gaat, d.w.z. (x+1 y) als dat aantal ± 1 is.
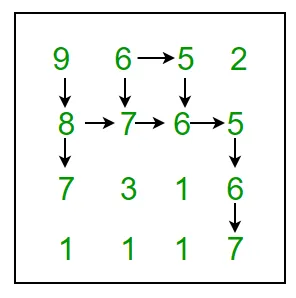
For example 9 6 5 2 8 7 6 5 7 3 1 6 1 1 1 7 In above grid the longest snake sequence is: (9 8 7 6 5 6 7)
Hieronder figuur toont alle mogelijke paden:

We raden u ten zeerste aan om uw browser te minimaliseren en dit eerst zelf te proberen.
Het idee is om dynamische programmering te gebruiken. Voor elke cel van de matrix behouden we de maximale lengte van een slang die eindigt in de huidige cel. De maximale lengte slangensequentie heeft een maximale waarde. De maximale waardecel komt overeen met de staart van de slang. Om de slang af te drukken, moeten we vanaf staart helemaal terug naar Snake's hoofd.
Let T[i][i] represent maximum length of a snake which ends at cell (i j) then for given matrix M the DP relation is defined as T[0][0] = 0 T[i][j] = max(T[i][j] T[i][j - 1] + 1) if M[i][j] = M[i][j - 1] ± 1 T[i][j] = max(T[i][j] T[i - 1][j] + 1) if M[i][j] = M[i - 1][j] ± 1
Hieronder is de implementatie van het idee
C++ // C++ program to find maximum length // Snake sequence and print it #include using namespace std ; #define M 4 #define N 4 struct Point { int x y ; }; // Function to find maximum length Snake sequence path // (i j) corresponds to tail of the snake list < Point > findPath ( int grid [ M ][ N ] int mat [ M ][ N ] int i int j ) { list < Point > path ; Point pt = { i j }; path . push_front ( pt ); while ( grid [ i ][ j ] != 0 ) { if ( i > 0 && grid [ i ][ j ] - 1 == grid [ i - 1 ][ j ]) { pt = { i - 1 j }; path . push_front ( pt ); i -- ; } else if ( j > 0 && grid [ i ][ j ] - 1 == grid [ i ][ j - 1 ]) { pt = { i j - 1 }; path . push_front ( pt ); j -- ; } } return path ; } // Function to find maximum length Snake sequence void findSnakeSequence ( int mat [ M ][ N ]) { // table to store results of subproblems int lookup [ M ][ N ]; // initialize by 0 memset ( lookup 0 sizeof lookup ); // stores maximum length of Snake sequence int max_len = 0 ; // store coordinates to snake's tail int max_row = 0 ; int max_col = 0 ; // fill the table in bottom-up fashion for ( int i = 0 ; i < M ; i ++ ) { for ( int j = 0 ; j < N ; j ++ ) { // do except for (0 0) cell if ( i || j ) { // look above if ( i > 0 && abs ( mat [ i - 1 ][ j ] - mat [ i ][ j ]) == 1 ) { lookup [ i ][ j ] = max ( lookup [ i ][ j ] lookup [ i - 1 ][ j ] + 1 ); if ( max_len < lookup [ i ][ j ]) { max_len = lookup [ i ][ j ]; max_row = i max_col = j ; } } // look left if ( j > 0 && abs ( mat [ i ][ j - 1 ] - mat [ i ][ j ]) == 1 ) { lookup [ i ][ j ] = max ( lookup [ i ][ j ] lookup [ i ][ j - 1 ] + 1 ); if ( max_len < lookup [ i ][ j ]) { max_len = lookup [ i ][ j ]; max_row = i max_col = j ; } } } } } cout < < 'Maximum length of Snake sequence is: ' < < max_len < < endl ; // find maximum length Snake sequence path list < Point > path = findPath ( lookup mat max_row max_col ); cout < < 'Snake sequence is:' ; for ( auto it = path . begin (); it != path . end (); it ++ ) cout < < endl < < mat [ it -> x ][ it -> y ] < < ' (' < < it -> x < < ' ' < < it -> y < < ')' ; } // Driver code int main () { int mat [ M ][ N ] = { { 9 6 5 2 } { 8 7 6 5 } { 7 3 1 6 } { 1 1 1 7 } }; findSnakeSequence ( mat ); return 0 ; }
Java // Java program to find maximum length // Snake sequence and print it import java.util.* ; class GFG { static int M = 4 ; static int N = 4 ; static class Point { int x y ; public Point ( int x int y ) { this . x = x ; this . y = y ; } }; // Function to find maximum length Snake sequence path // (i j) corresponds to tail of the snake static List < Point > findPath ( int grid [][] int mat [][] int i int j ) { List < Point > path = new LinkedList <> (); Point pt = new Point ( i j ); path . add ( 0 pt ); while ( grid [ i ][ j ] != 0 ) { if ( i > 0 && grid [ i ][ j ] - 1 == grid [ i - 1 ][ j ] ) { pt = new Point ( i - 1 j ); path . add ( 0 pt ); i -- ; } else if ( j > 0 && grid [ i ][ j ] - 1 == grid [ i ][ j - 1 ] ) { pt = new Point ( i j - 1 ); path . add ( 0 pt ); j -- ; } } return path ; } // Function to find maximum length Snake sequence static void findSnakeSequence ( int mat [][] ) { // table to store results of subproblems int [][] lookup = new int [ M ][ N ] ; // initialize by 0 // stores maximum length of Snake sequence int max_len = 0 ; // store coordinates to snake's tail int max_row = 0 ; int max_col = 0 ; // fill the table in bottom-up fashion for ( int i = 0 ; i < M ; i ++ ) { for ( int j = 0 ; j < N ; j ++ ) { // do except for (0 0) cell if ( i != 0 || j != 0 ) { // look above if ( i > 0 && Math . abs ( mat [ i - 1 ][ j ] - mat [ i ][ j ] ) == 1 ) { lookup [ i ][ j ] = Math . max ( lookup [ i ][ j ] lookup [ i - 1 ][ j ] + 1 ); if ( max_len < lookup [ i ][ j ] ) { max_len = lookup [ i ][ j ] ; max_row = i ; max_col = j ; } } // look left if ( j > 0 && Math . abs ( mat [ i ][ j - 1 ] - mat [ i ][ j ] ) == 1 ) { lookup [ i ][ j ] = Math . max ( lookup [ i ][ j ] lookup [ i ][ j - 1 ] + 1 ); if ( max_len < lookup [ i ][ j ] ) { max_len = lookup [ i ][ j ] ; max_row = i ; max_col = j ; } } } } } System . out . print ( 'Maximum length of Snake ' + 'sequence is: ' + max_len + 'n' ); // find maximum length Snake sequence path List < Point > path = findPath ( lookup mat max_row max_col ); System . out . print ( 'Snake sequence is:' ); for ( Point it : path ) System . out . print ( 'n' + mat [ it . x ][ it . y ] + ' (' + it . x + ' ' + it . y + ')' ); } // Driver code public static void main ( String [] args ) { int mat [][] = {{ 9 6 5 2 } { 8 7 6 5 } { 7 3 1 6 } { 1 1 1 7 }}; findSnakeSequence ( mat ); } } // This code is contributed by 29AjayKumar
C# // C# program to find maximum length // Snake sequence and print it using System ; using System.Collections.Generic ; class GFG { static int M = 4 ; static int N = 4 ; public class Point { public int x y ; public Point ( int x int y ) { this . x = x ; this . y = y ; } }; // Function to find maximum length Snake sequence path // (i j) corresponds to tail of the snake static List < Point > findPath ( int [ ] grid int [ ] mat int i int j ) { List < Point > path = new List < Point > (); Point pt = new Point ( i j ); path . Insert ( 0 pt ); while ( grid [ i j ] != 0 ) { if ( i > 0 && grid [ i j ] - 1 == grid [ i - 1 j ]) { pt = new Point ( i - 1 j ); path . Insert ( 0 pt ); i -- ; } else if ( j > 0 && grid [ i j ] - 1 == grid [ i j - 1 ]) { pt = new Point ( i j - 1 ); path . Insert ( 0 pt ); j -- ; } } return path ; } // Function to find maximum length Snake sequence static void findSnakeSequence ( int [ ] mat ) { // table to store results of subproblems int [ ] lookup = new int [ M N ]; // initialize by 0 // stores maximum length of Snake sequence int max_len = 0 ; // store coordinates to snake's tail int max_row = 0 ; int max_col = 0 ; // fill the table in bottom-up fashion for ( int i = 0 ; i < M ; i ++ ) { for ( int j = 0 ; j < N ; j ++ ) { // do except for (0 0) cell if ( i != 0 || j != 0 ) { // look above if ( i > 0 && Math . Abs ( mat [ i - 1 j ] - mat [ i j ]) == 1 ) { lookup [ i j ] = Math . Max ( lookup [ i j ] lookup [ i - 1 j ] + 1 ); if ( max_len < lookup [ i j ]) { max_len = lookup [ i j ]; max_row = i ; max_col = j ; } } // look left if ( j > 0 && Math . Abs ( mat [ i j - 1 ] - mat [ i j ]) == 1 ) { lookup [ i j ] = Math . Max ( lookup [ i j ] lookup [ i j - 1 ] + 1 ); if ( max_len < lookup [ i j ]) { max_len = lookup [ i j ]; max_row = i ; max_col = j ; } } } } } Console . Write ( 'Maximum length of Snake ' + 'sequence is: ' + max_len + 'n' ); // find maximum length Snake sequence path List < Point > path = findPath ( lookup mat max_row max_col ); Console . Write ( 'Snake sequence is:' ); foreach ( Point it in path ) Console . Write ( 'n' + mat [ it . x it . y ] + ' (' + it . x + ' ' + it . y + ')' ); } // Driver code public static void Main ( String [] args ) { int [ ] mat = { { 9 6 5 2 } { 8 7 6 5 } { 7 3 1 6 } { 1 1 1 7 } }; findSnakeSequence ( mat ); } } // This code is contributed by Princi Singh
Python3 def snakesequence ( S m n ): sequence = {} DP = [[ 1 for x in range ( m + 1 )] for x in range ( n + 1 )] a b maximum = 0 0 0 position = [ 0 0 ] for i in range ( 0 n + 1 ): for j in range ( 0 m + 1 ): a b = 0 0 p = 'initial' if ( i > 0 and abs ( S [ i ][ j ] - S [ i - 1 ][ j ]) == 1 ): a = DP [ i - 1 ][ j ] if ( j > 0 and abs ( S [ i ][ j ] - S [ i ][ j - 1 ]) == 1 ): b = DP [ i ][ j - 1 ] if a != 0 and a >= b : p = str ( i - 1 ) + ' ' + str ( j ) elif b != 0 : p = str ( i ) + ' ' + str ( j - 1 ) q = str ( i ) + ' ' + str ( j ) sequence [ q ] = p DP [ i ][ j ] = DP [ i ][ j ] + max ( a b ) if DP [ i ][ j ] >= maximum : maximum = DP [ i ][ j ] position [ 0 ] = i position [ 1 ] = j snakeValues = [] snakePositions = [] snakeValues . append ( S [ position [ 0 ]][ position [ 1 ]]) check = 'found' str_next = str ( position [ 0 ]) + ' ' + str ( position [ 1 ]) findingIndices = sequence [ str_next ] . split () while ( check == 'found' ): if sequence [ str_next ] == 'initial' : snakePositions . insert ( 0 str_next ) check = 'end' continue findingIndices = sequence [ str_next ] . split () g = int ( findingIndices [ 0 ]) h = int ( findingIndices [ 1 ]) snakeValues . insert ( 0 S [ g ][ h ]) snake_position = str ( g ) + ' ' + str ( h ) snakePositions . insert ( 0 str_next ) str_next = sequence [ str_next ] return [ snakeValues snakePositions ] S = [[ 9 6 5 2 ] [ 8 7 6 5 ] [ 7 3 1 6 ] [ 1 1 10 7 ]] m = 3 n = 3 seq = snakesequence ( S m n ) for i in range ( len ( seq [ 0 ])): print ( seq [ 0 ][ i ] '' seq [ 1 ][ i ] . split ())
JavaScript function snakesequence ( S m n ) { let sequence = {} let DP = new Array ( n + 1 ) for ( var i = 0 ; i <= n ; i ++ ) DP [ i ] = new Array ( m + 1 ). fill ( 1 ) let a = 0 b = 0 maximum = 0 let position = [ 0 0 ] for ( var i = 0 ; i <= n ; i ++ ) { for ( var j = 0 ; j <= m ; j ++ ) { a = 0 b = 0 let p = 'initial' if ( i > 0 && Math . abs ( S [ i ][ j ] - S [ i - 1 ][ j ]) == 1 ) a = DP [ i - 1 ][ j ] if ( j > 0 && Math . abs ( S [ i ][ j ] - S [ i ][ j - 1 ]) == 1 ) b = DP [ i ][ j - 1 ] if ( a != 0 && a >= b ) p = String ( i - 1 ) + ' ' + String ( j ) else if ( b != 0 ) p = String ( i ) + ' ' + String ( j - 1 ) let q = String ( i ) + ' ' + String ( j ) sequence [ q ] = p DP [ i ][ j ] = DP [ i ][ j ] + Math . max ( a b ) if ( DP [ i ][ j ] >= maximum ) { maximum = DP [ i ][ j ] position [ 0 ] = i position [ 1 ] = j } } } let snakeValues = [] let snakePositions = [] snakeValues . push ( S [ position [ 0 ]][ position [ 1 ]]) let check = 'found' let String_next = String ( position [ 0 ]) + ' ' + String ( position [ 1 ]) let findingIndices = sequence [ String_next ]. split ( ' ' ) while ( check == 'found' ) { if ( sequence [ String_next ] == 'initial' ) { snakePositions . unshift ( String_next ) check = 'end' continue } findingIndices = sequence [ String_next ]. split ( ' ' ) let g = parseInt ( findingIndices [ 0 ]) let h = parseInt ( findingIndices [ 1 ]) snakeValues . unshift ( S [ g ][ h ]) let snake_position = String ( g ) + ' ' + String ( h ) snakePositions . unshift ( String_next ) String_next = sequence [ String_next ] } return [ snakeValues snakePositions ] } // Driver Code let S = [[ 9 6 5 2 ] [ 8 7 6 5 ] [ 7 3 1 6 ] [ 1 1 10 7 ]] let m = 3 let n = 3 let seq = snakesequence ( S m n ) for ( var i = 0 ; i < seq [ 0 ]. length ; i ++ ) console . log ( seq [ 0 ][ i ] + '' seq [ 1 ][ i ]. split ( ' ' ))
Uitvoer
Maximum length of Snake sequence is: 6 Snake sequence is: 9 (0 0) 8 (1 0) 7 (1 1) 6 (1 2) 5 (1 3) 6 (2 3) 7 (3 3)
Tijdcomplexiteit van bovenstaande oplossing is O (M*N). Hulpruimte die wordt gebruikt door bovenstaande oplossing is O (m*n). Als we niet verplicht zijn om af te drukken, kan de slangenruimte verder worden gereduceerd tot O (n), omdat we alleen het resultaat van de laatste rij gebruiken.