지점과 구속을 사용하는 여행 세일즈맨 문제

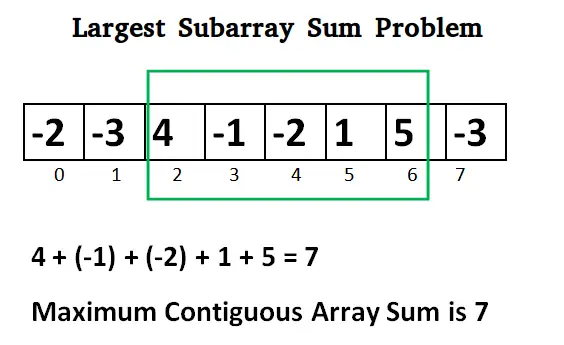
도시 세트와 모든 도시 쌍 사이의 거리가 주어지면 문제는 모든 도시를 정확히 한 번 방문하고 출발점으로 돌아갈 수있는 가장 짧은 투어를 찾는 것입니다.

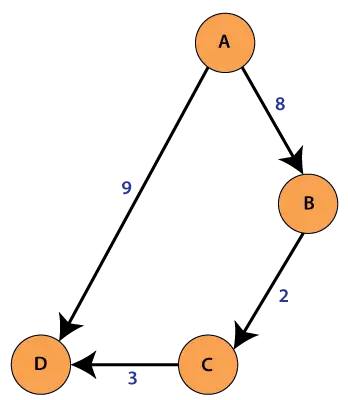
예를 들어 오른쪽 그림에 표시된 그래프를 고려하십시오. 그래프의 TSP 투어는 0-1-3-2-0입니다. 투어 비용은 10+25+30+15로 80입니다.
우리는 다음에 다음을 논의했습니다
1) 순진하고 역동적 인 프로그래밍
2) MST를 사용한 대략적인 솔루션
분기 및 바운드 솔루션
트리의 전류 노드에 대한 분기 및 바운드 메소드의 이전 기사에서 볼 수 있듯이이 노드를 아래로 내릴 경우 얻을 수있는 최상의 가능한 솔루션에 대한 바운드를 계산합니다. 최상의 가능한 솔루션 자체에 대한 바운드가 현재 최고보다 나쁘면 (지금까지 최고의 계산) 노드가 뿌리 내린 하위 트리를 무시합니다.
노드를 통한 비용에는 두 가지 비용이 포함됩니다.
1) 루트에서 노드에 도달하는 비용 (노드에 도달하면이 비용이 계산됩니다).
2) 현재 노드에서 잎으로 답변하는 비용 (이 노드로 하위 트리를 무시할지 여부를 결정하기 위해이 비용에 대한 경계를 계산합니다).
- a 최대화 문제 상한은 주어진 노드를 따르는 경우 가능한 최대 솔루션을 알려줍니다. 예를 들어 0/1 Knapsack 우리는 욕심 많은 접근법을 사용하여 상한을 찾았습니다. .
- a 최소화 문제 하한은 주어진 노드를 따르는 경우 가능한 최소 솔루션을 알려줍니다. 예를 들어 작업 할당 문제 우리는 근로자에게 최소 비용 직업을 할당함으로써 하한을 얻습니다.
지점과 묶음에서 도전적인 부분은 가능한 최상의 솔루션에 대한 바운드를 계산하는 방법을 찾는 것입니다. 아래는 여행 판매원 문제에 대한 경계를 계산하는 데 사용되는 아이디어입니다.
모든 투어 비용은 다음과 같이 작성할 수 있습니다.
Cost of a tour T = (1/2) * ? (Sum of cost of two edges adjacent to u and in the tour T) where u ? V For every vertex u if we consider two edges through it in T and sum their costs. The overall sum for all vertices would be twice of cost of tour T (We have considered every edge twice.) (Sum of two tour edges adjacent to u) >= (sum of minimum weight two edges adjacent to u) Cost of any tour >= 1/2) * ? (Sum of cost of two minimum weight edges adjacent to u) where u ? V
예를 들어 위의 그림 그래프를 고려하십시오. 다음은 모든 노드에 인접한 최소 2 개의 가장자리입니다.
Node Least cost edges Total cost 0 (0 1) (0 2) 25 1 (0 1) (1 3) 35 2 (0 2) (2 3) 45 3 (0 3) (1 3) 45 Thus a lower bound on the cost of any tour = 1/2(25 + 35 + 45 + 45) = 75 Refer this for one more example.
이제 우리는 하한 계산에 대한 아이디어가 있습니다. 상태 공간 검색 트리를 적용하는 방법을 살펴 보겠습니다. 우리는 가능한 모든 노드를 열거하기 시작합니다 (바람직하게는 사전 순서로)
1. 루트 노드 : 일반적인 손실없이 우리는 하한이 상기 계산 된 Vertex '0'에서 시작한다고 가정합니다.
레벨 2를 다루기 : 다음 레벨은 우리가 갈 수있는 모든 가능한 정점을 열거하고 (어떤 경로에서든 정점은 한 번만 발생해야한다는 점을 명심하십시오)는 1 2 3 ... n입니다 (그래프가 완료됨). 우리가 0에서 1으로 이동했기 때문에 정점 1을 계산하는 것을 고려하십시오. 투어에는 이제 Edge 0-1이 포함되었습니다. 이를 통해 루트의 하한을 변경할 수 있습니다.
Lower Bound for vertex 1 = Old lower bound - ((minimum edge cost of 0 + minimum edge cost of 1) / 2) + (edge cost 0-1)
어떻게 작동합니까? 모서리 0-1을 포함시키기 위해 가장자리 비용 0-1의 가장자리 비용을 추가하고 하한 무게를 감격하여 최소한이 단단하게 유지되므로 0과 1의 최소 모서리의 합이 2로 나뉩니다.
다른 수준 처리 : 우리가 다음 단계로 넘어 가면서 우리는 다시 가능한 모든 정점을 열거합니다. 위의 경우 1 이후에 더 나아가는 경우 2 3 4 ... n을 확인합니다.
1에서 1로 이동함에 따라 2의 하한을 고려하십시오. Edge 1-2를 투어로 포함 하고이 노드의 새로운 하한을 변경하십시오.
Lower bound(2) = Old lower bound - ((second minimum edge cost of 1 + minimum edge cost of 2)/2) + edge cost 1-2)
참고 : 공식의 유일한 변화는 이번에는 최소 에지 비용이 이미 이전 수준에서 빼기 때문에 1에 대한 두 번째 최소 에지 비용이 포함된다는 것입니다.
// C++ program to solve Traveling Salesman Problem // using Branch and Bound. #include using namespace std ; const int N = 4 ; // final_path[] stores the final solution ie the // path of the salesman. int final_path [ N + 1 ]; // visited[] keeps track of the already visited nodes // in a particular path bool visited [ N ]; // Stores the final minimum weight of shortest tour. int final_res = INT_MAX ; // Function to copy temporary solution to // the final solution void copyToFinal ( int curr_path []) { for ( int i = 0 ; i < N ; i ++ ) final_path [ i ] = curr_path [ i ]; final_path [ N ] = curr_path [ 0 ]; } // Function to find the minimum edge cost // having an end at the vertex i int firstMin ( int adj [ N ][ N ] int i ) { int min = INT_MAX ; for ( int k = 0 ; k < N ; k ++ ) if ( adj [ i ][ k ] < min && i != k ) min = adj [ i ][ k ]; return min ; } // function to find the second minimum edge cost // having an end at the vertex i int secondMin ( int adj [ N ][ N ] int i ) { int first = INT_MAX second = INT_MAX ; for ( int j = 0 ; j < N ; j ++ ) { if ( i == j ) continue ; if ( adj [ i ][ j ] <= first ) { second = first ; first = adj [ i ][ j ]; } else if ( adj [ i ][ j ] <= second && adj [ i ][ j ] != first ) second = adj [ i ][ j ]; } return second ; } // function that takes as arguments: // curr_bound -> lower bound of the root node // curr_weight-> stores the weight of the path so far // level-> current level while moving in the search // space tree // curr_path[] -> where the solution is being stored which // would later be copied to final_path[] void TSPRec ( int adj [ N ][ N ] int curr_bound int curr_weight int level int curr_path []) { // base case is when we have reached level N which // means we have covered all the nodes once if ( level == N ) { // check if there is an edge from last vertex in // path back to the first vertex if ( adj [ curr_path [ level -1 ]][ curr_path [ 0 ]] != 0 ) { // curr_res has the total weight of the // solution we got int curr_res = curr_weight + adj [ curr_path [ level -1 ]][ curr_path [ 0 ]]; // Update final result and final path if // current result is better. if ( curr_res < final_res ) { copyToFinal ( curr_path ); final_res = curr_res ; } } return ; } // for any other level iterate for all vertices to // build the search space tree recursively for ( int i = 0 ; i < N ; i ++ ) { // Consider next vertex if it is not same (diagonal // entry in adjacency matrix and not visited // already) if ( adj [ curr_path [ level -1 ]][ i ] != 0 && visited [ i ] == false ) { int temp = curr_bound ; curr_weight += adj [ curr_path [ level -1 ]][ i ]; // different computation of curr_bound for // level 2 from the other levels if ( level == 1 ) curr_bound -= (( firstMin ( adj curr_path [ level -1 ]) + firstMin ( adj i )) / 2 ); else curr_bound -= (( secondMin ( adj curr_path [ level -1 ]) + firstMin ( adj i )) / 2 ); // curr_bound + curr_weight is the actual lower bound // for the node that we have arrived on // If current lower bound < final_res we need to explore // the node further if ( curr_bound + curr_weight < final_res ) { curr_path [ level ] = i ; visited [ i ] = true ; // call TSPRec for the next level TSPRec ( adj curr_bound curr_weight level + 1 curr_path ); } // Else we have to prune the node by resetting // all changes to curr_weight and curr_bound curr_weight -= adj [ curr_path [ level -1 ]][ i ]; curr_bound = temp ; // Also reset the visited array memset ( visited false sizeof ( visited )); for ( int j = 0 ; j <= level -1 ; j ++ ) visited [ curr_path [ j ]] = true ; } } } // This function sets up final_path[] void TSP ( int adj [ N ][ N ]) { int curr_path [ N + 1 ]; // Calculate initial lower bound for the root node // using the formula 1/2 * (sum of first min + // second min) for all edges. // Also initialize the curr_path and visited array int curr_bound = 0 ; memset ( curr_path -1 sizeof ( curr_path )); memset ( visited 0 sizeof ( curr_path )); // Compute initial bound for ( int i = 0 ; i < N ; i ++ ) curr_bound += ( firstMin ( adj i ) + secondMin ( adj i )); // Rounding off the lower bound to an integer curr_bound = ( curr_bound & 1 ) ? curr_bound / 2 + 1 : curr_bound / 2 ; // We start at vertex 1 so the first vertex // in curr_path[] is 0 visited [ 0 ] = true ; curr_path [ 0 ] = 0 ; // Call to TSPRec for curr_weight equal to // 0 and level 1 TSPRec ( adj curr_bound 0 1 curr_path ); } // Driver code int main () { //Adjacency matrix for the given graph int adj [ N ][ N ] = { { 0 10 15 20 } { 10 0 35 25 } { 15 35 0 30 } { 20 25 30 0 } }; TSP ( adj ); printf ( 'Minimum cost : %d n ' final_res ); printf ( 'Path Taken : ' ); for ( int i = 0 ; i <= N ; i ++ ) printf ( '%d ' final_path [ i ]); return 0 ; }
Java // Java program to solve Traveling Salesman Problem // using Branch and Bound. import java.util.* ; class GFG { static int N = 4 ; // final_path[] stores the final solution ie the // path of the salesman. static int final_path [] = new int [ N + 1 ] ; // visited[] keeps track of the already visited nodes // in a particular path static boolean visited [] = new boolean [ N ] ; // Stores the final minimum weight of shortest tour. static int final_res = Integer . MAX_VALUE ; // Function to copy temporary solution to // the final solution static void copyToFinal ( int curr_path [] ) { for ( int i = 0 ; i < N ; i ++ ) final_path [ i ] = curr_path [ i ] ; final_path [ N ] = curr_path [ 0 ] ; } // Function to find the minimum edge cost // having an end at the vertex i static int firstMin ( int adj [][] int i ) { int min = Integer . MAX_VALUE ; for ( int k = 0 ; k < N ; k ++ ) if ( adj [ i ][ k ] < min && i != k ) min = adj [ i ][ k ] ; return min ; } // function to find the second minimum edge cost // having an end at the vertex i static int secondMin ( int adj [][] int i ) { int first = Integer . MAX_VALUE second = Integer . MAX_VALUE ; for ( int j = 0 ; j < N ; j ++ ) { if ( i == j ) continue ; if ( adj [ i ][ j ] <= first ) { second = first ; first = adj [ i ][ j ] ; } else if ( adj [ i ][ j ] <= second && adj [ i ][ j ] != first ) second = adj [ i ][ j ] ; } return second ; } // function that takes as arguments: // curr_bound -> lower bound of the root node // curr_weight-> stores the weight of the path so far // level-> current level while moving in the search // space tree // curr_path[] -> where the solution is being stored which // would later be copied to final_path[] static void TSPRec ( int adj [][] int curr_bound int curr_weight int level int curr_path [] ) { // base case is when we have reached level N which // means we have covered all the nodes once if ( level == N ) { // check if there is an edge from last vertex in // path back to the first vertex if ( adj [ curr_path [ level - 1 ]][ curr_path [ 0 ]] != 0 ) { // curr_res has the total weight of the // solution we got int curr_res = curr_weight + adj [ curr_path [ level - 1 ]][ curr_path [ 0 ]] ; // Update final result and final path if // current result is better. if ( curr_res < final_res ) { copyToFinal ( curr_path ); final_res = curr_res ; } } return ; } // for any other level iterate for all vertices to // build the search space tree recursively for ( int i = 0 ; i < N ; i ++ ) { // Consider next vertex if it is not same (diagonal // entry in adjacency matrix and not visited // already) if ( adj [ curr_path [ level - 1 ]][ i ] != 0 && visited [ i ] == false ) { int temp = curr_bound ; curr_weight += adj [ curr_path [ level - 1 ]][ i ] ; // different computation of curr_bound for // level 2 from the other levels if ( level == 1 ) curr_bound -= (( firstMin ( adj curr_path [ level - 1 ] ) + firstMin ( adj i )) / 2 ); else curr_bound -= (( secondMin ( adj curr_path [ level - 1 ] ) + firstMin ( adj i )) / 2 ); // curr_bound + curr_weight is the actual lower bound // for the node that we have arrived on // If current lower bound < final_res we need to explore // the node further if ( curr_bound + curr_weight < final_res ) { curr_path [ level ] = i ; visited [ i ] = true ; // call TSPRec for the next level TSPRec ( adj curr_bound curr_weight level + 1 curr_path ); } // Else we have to prune the node by resetting // all changes to curr_weight and curr_bound curr_weight -= adj [ curr_path [ level - 1 ]][ i ] ; curr_bound = temp ; // Also reset the visited array Arrays . fill ( visited false ); for ( int j = 0 ; j <= level - 1 ; j ++ ) visited [ curr_path [ j ]] = true ; } } } // This function sets up final_path[] static void TSP ( int adj [][] ) { int curr_path [] = new int [ N + 1 ] ; // Calculate initial lower bound for the root node // using the formula 1/2 * (sum of first min + // second min) for all edges. // Also initialize the curr_path and visited array int curr_bound = 0 ; Arrays . fill ( curr_path - 1 ); Arrays . fill ( visited false ); // Compute initial bound for ( int i = 0 ; i < N ; i ++ ) curr_bound += ( firstMin ( adj i ) + secondMin ( adj i )); // Rounding off the lower bound to an integer curr_bound = ( curr_bound == 1 ) ? curr_bound / 2 + 1 : curr_bound / 2 ; // We start at vertex 1 so the first vertex // in curr_path[] is 0 visited [ 0 ] = true ; curr_path [ 0 ] = 0 ; // Call to TSPRec for curr_weight equal to // 0 and level 1 TSPRec ( adj curr_bound 0 1 curr_path ); } // Driver code public static void main ( String [] args ) { //Adjacency matrix for the given graph int adj [][] = {{ 0 10 15 20 } { 10 0 35 25 } { 15 35 0 30 } { 20 25 30 0 } }; TSP ( adj ); System . out . printf ( 'Minimum cost : %dn' final_res ); System . out . printf ( 'Path Taken : ' ); for ( int i = 0 ; i <= N ; i ++ ) { System . out . printf ( '%d ' final_path [ i ] ); } } } /* This code contributed by PrinciRaj1992 */
Python3 # Python3 program to solve # Traveling Salesman Problem using # Branch and Bound. import math maxsize = float ( 'inf' ) # Function to copy temporary solution # to the final solution def copyToFinal ( curr_path ): final_path [: N + 1 ] = curr_path [:] final_path [ N ] = curr_path [ 0 ] # Function to find the minimum edge cost # having an end at the vertex i def firstMin ( adj i ): min = maxsize for k in range ( N ): if adj [ i ][ k ] < min and i != k : min = adj [ i ][ k ] return min # function to find the second minimum edge # cost having an end at the vertex i def secondMin ( adj i ): first second = maxsize maxsize for j in range ( N ): if i == j : continue if adj [ i ][ j ] <= first : second = first first = adj [ i ][ j ] elif ( adj [ i ][ j ] <= second and adj [ i ][ j ] != first ): second = adj [ i ][ j ] return second # function that takes as arguments: # curr_bound -> lower bound of the root node # curr_weight-> stores the weight of the path so far # level-> current level while moving # in the search space tree # curr_path[] -> where the solution is being stored # which would later be copied to final_path[] def TSPRec ( adj curr_bound curr_weight level curr_path visited ): global final_res # base case is when we have reached level N # which means we have covered all the nodes once if level == N : # check if there is an edge from # last vertex in path back to the first vertex if adj [ curr_path [ level - 1 ]][ curr_path [ 0 ]] != 0 : # curr_res has the total weight # of the solution we got curr_res = curr_weight + adj [ curr_path [ level - 1 ]] [ curr_path [ 0 ]] if curr_res < final_res : copyToFinal ( curr_path ) final_res = curr_res return # for any other level iterate for all vertices # to build the search space tree recursively for i in range ( N ): # Consider next vertex if it is not same # (diagonal entry in adjacency matrix and # not visited already) if ( adj [ curr_path [ level - 1 ]][ i ] != 0 and visited [ i ] == False ): temp = curr_bound curr_weight += adj [ curr_path [ level - 1 ]][ i ] # different computation of curr_bound # for level 2 from the other levels if level == 1 : curr_bound -= (( firstMin ( adj curr_path [ level - 1 ]) + firstMin ( adj i )) / 2 ) else : curr_bound -= (( secondMin ( adj curr_path [ level - 1 ]) + firstMin ( adj i )) / 2 ) # curr_bound + curr_weight is the actual lower bound # for the node that we have arrived on. # If current lower bound < final_res # we need to explore the node further if curr_bound + curr_weight < final_res : curr_path [ level ] = i visited [ i ] = True # call TSPRec for the next level TSPRec ( adj curr_bound curr_weight level + 1 curr_path visited ) # Else we have to prune the node by resetting # all changes to curr_weight and curr_bound curr_weight -= adj [ curr_path [ level - 1 ]][ i ] curr_bound = temp # Also reset the visited array visited = [ False ] * len ( visited ) for j in range ( level ): if curr_path [ j ] != - 1 : visited [ curr_path [ j ]] = True # This function sets up final_path def TSP ( adj ): # Calculate initial lower bound for the root node # using the formula 1/2 * (sum of first min + # second min) for all edges. Also initialize the # curr_path and visited array curr_bound = 0 curr_path = [ - 1 ] * ( N + 1 ) visited = [ False ] * N # Compute initial bound for i in range ( N ): curr_bound += ( firstMin ( adj i ) + secondMin ( adj i )) # Rounding off the lower bound to an integer curr_bound = math . ceil ( curr_bound / 2 ) # We start at vertex 1 so the first vertex # in curr_path[] is 0 visited [ 0 ] = True curr_path [ 0 ] = 0 # Call to TSPRec for curr_weight # equal to 0 and level 1 TSPRec ( adj curr_bound 0 1 curr_path visited ) # Driver code # Adjacency matrix for the given graph adj = [[ 0 10 15 20 ] [ 10 0 35 25 ] [ 15 35 0 30 ] [ 20 25 30 0 ]] N = 4 # final_path[] stores the final solution # i.e. the // path of the salesman. final_path = [ None ] * ( N + 1 ) # visited[] keeps track of the already # visited nodes in a particular path visited = [ False ] * N # Stores the final minimum weight # of shortest tour. final_res = maxsize TSP ( adj ) print ( 'Minimum cost :' final_res ) print ( 'Path Taken : ' end = ' ' ) for i in range ( N + 1 ): print ( final_path [ i ] end = ' ' ) # This code is contributed by ng24_7
C# // C# program to solve Traveling Salesman Problem // using Branch and Bound. using System ; public class GFG { static int N = 4 ; // final_path[] stores the final solution ie the // path of the salesman. static int [] final_path = new int [ N + 1 ]; // visited[] keeps track of the already visited nodes // in a particular path static bool [] visited = new bool [ N ]; // Stores the final minimum weight of shortest tour. static int final_res = Int32 . MaxValue ; // Function to copy temporary solution to // the final solution static void copyToFinal ( int [] curr_path ) { for ( int i = 0 ; i < N ; i ++ ) final_path [ i ] = curr_path [ i ]; final_path [ N ] = curr_path [ 0 ]; } // Function to find the minimum edge cost // having an end at the vertex i static int firstMin ( int [ ] adj int i ) { int min = Int32 . MaxValue ; for ( int k = 0 ; k < N ; k ++ ) if ( adj [ i k ] < min && i != k ) min = adj [ i k ]; return min ; } // function to find the second minimum edge cost // having an end at the vertex i static int secondMin ( int [ ] adj int i ) { int first = Int32 . MaxValue second = Int32 . MaxValue ; for ( int j = 0 ; j < N ; j ++ ) { if ( i == j ) continue ; if ( adj [ i j ] <= first ) { second = first ; first = adj [ i j ]; } else if ( adj [ i j ] <= second && adj [ i j ] != first ) second = adj [ i j ]; } return second ; } // function that takes as arguments: // curr_bound -> lower bound of the root node // curr_weight-> stores the weight of the path so far // level-> current level while moving in the search // space tree // curr_path[] -> where the solution is being stored // which // would later be copied to final_path[] static void TSPRec ( int [ ] adj int curr_bound int curr_weight int level int [] curr_path ) { // base case is when we have reached level N which // means we have covered all the nodes once if ( level == N ) { // check if there is an edge from last vertex in // path back to the first vertex if ( adj [ curr_path [ level - 1 ] curr_path [ 0 ]] != 0 ) { // curr_res has the total weight of the // solution we got int curr_res = curr_weight + adj [ curr_path [ level - 1 ] curr_path [ 0 ]]; // Update final result and final path if // current result is better. if ( curr_res < final_res ) { copyToFinal ( curr_path ); final_res = curr_res ; } } return ; } // for any other level iterate for all vertices to // build the search space tree recursively for ( int i = 0 ; i < N ; i ++ ) { // Consider next vertex if it is not same // (diagonal entry in adjacency matrix and not // visited already) if ( adj [ curr_path [ level - 1 ] i ] != 0 && visited [ i ] == false ) { int temp = curr_bound ; curr_weight += adj [ curr_path [ level - 1 ] i ]; // different computation of curr_bound for // level 2 from the other levels if ( level == 1 ) curr_bound -= (( firstMin ( adj curr_path [ level - 1 ]) + firstMin ( adj i )) / 2 ); else curr_bound -= (( secondMin ( adj curr_path [ level - 1 ]) + firstMin ( adj i )) / 2 ); // curr_bound + curr_weight is the actual // lower bound for the node that we have // arrived on If current lower bound < // final_res we need to explore the node // further if ( curr_bound + curr_weight < final_res ) { curr_path [ level ] = i ; visited [ i ] = true ; // call TSPRec for the next level TSPRec ( adj curr_bound curr_weight level + 1 curr_path ); } // Else we have to prune the node by // resetting all changes to curr_weight and // curr_bound curr_weight -= adj [ curr_path [ level - 1 ] i ]; curr_bound = temp ; // Also reset the visited array Array . Fill ( visited false ); for ( int j = 0 ; j <= level - 1 ; j ++ ) visited [ curr_path [ j ]] = true ; } } } // This function sets up final_path[] static void TSP ( int [ ] adj ) { int [] curr_path = new int [ N + 1 ]; // Calculate initial lower bound for the root node // using the formula 1/2 * (sum of first min + // second min) for all edges. // Also initialize the curr_path and visited array int curr_bound = 0 ; Array . Fill ( curr_path - 1 ); Array . Fill ( visited false ); // Compute initial bound for ( int i = 0 ; i < N ; i ++ ) curr_bound += ( firstMin ( adj i ) + secondMin ( adj i )); // Rounding off the lower bound to an integer curr_bound = ( curr_bound == 1 ) ? curr_bound / 2 + 1 : curr_bound / 2 ; // We start at vertex 1 so the first vertex // in curr_path[] is 0 visited [ 0 ] = true ; curr_path [ 0 ] = 0 ; // Call to TSPRec for curr_weight equal to // 0 and level 1 TSPRec ( adj curr_bound 0 1 curr_path ); } // Driver code static public void Main () { // Adjacency matrix for the given graph int [ ] adj = { { 0 10 15 20 } { 10 0 35 25 } { 15 35 0 30 } { 20 25 30 0 } }; TSP ( adj ); Console . WriteLine ( 'Minimum cost : ' + final_res ); Console . Write ( 'Path Taken : ' ); for ( int i = 0 ; i <= N ; i ++ ) { Console . Write ( final_path [ i ] + ' ' ); } } } // This code is contributed by Rohit Pradhan
JavaScript const N = 4 ; // final_path[] stores the final solution ie the // path of the salesman. let final_path = Array ( N + 1 ). fill ( - 1 ); // visited[] keeps track of the already visited nodes // in a particular path let visited = Array ( N ). fill ( false ); // Stores the final minimum weight of shortest tour. let final_res = Number . MAX_SAFE_INTEGER ; // Function to copy temporary solution to // the final solution function copyToFinal ( curr_path ){ for ( let i = 0 ; i < N ; i ++ ){ final_path [ i ] = curr_path [ i ]; } final_path [ N ] = curr_path [ 0 ]; } // Function to find the minimum edge cost // having an end at the vertex i function firstMin ( adj i ){ let min = Number . MAX_SAFE_INTEGER ; for ( let k = 0 ; k < N ; k ++ ){ if ( adj [ i ][ k ] < min && i !== k ){ min = adj [ i ][ k ]; } } return min ; } // function to find the second minimum edge cost // having an end at the vertex i function secondMin ( adj i ){ let first = Number . MAX_SAFE_INTEGER ; let second = Number . MAX_SAFE_INTEGER ; for ( let j = 0 ; j < N ; j ++ ){ if ( i == j ){ continue ; } if ( adj [ i ][ j ] <= first ){ second = first ; first = adj [ i ][ j ]; } else if ( adj [ i ][ j ] <= second && adj [ i ][ j ] !== first ){ second = adj [ i ][ j ]; } } return second ; } // function that takes as arguments: // curr_bound -> lower bound of the root node // curr_weight-> stores the weight of the path so far // level-> current level while moving in the search // space tree // curr_path[] -> where the solution is being stored which // would later be copied to final_path[] function TSPRec ( adj curr_bound curr_weight level curr_path ) { // base case is when we have reached level N which // means we have covered all the nodes once if ( level == N ) { // check if there is an edge from last vertex in // path back to the first vertex if ( adj [ curr_path [ level - 1 ]][ curr_path [ 0 ]] !== 0 ) { // curr_res has the total weight of the // solution we got let curr_res = curr_weight + adj [ curr_path [ level - 1 ]][ curr_path [ 0 ]]; // Update final result and final path if // current result is better. if ( curr_res < final_res ) { copyToFinal ( curr_path ); final_res = curr_res ; } } return ; } // for any other level iterate for all vertices to // build the search space tree recursively for ( let i = 0 ; i < N ; i ++ ){ // Consider next vertex if it is not same (diagonal // entry in adjacency matrix and not visited // already) if ( adj [ curr_path [ level - 1 ]][ i ] !== 0 && ! visited [ i ]){ let temp = curr_bound ; curr_weight += adj [ curr_path [ level - 1 ]][ i ]; // different computation of curr_bound for // level 2 from the other levels if ( level == 1 ){ curr_bound -= ( firstMin ( adj curr_path [ level - 1 ]) + firstMin ( adj i )) / 2 ; } else { curr_bound -= ( secondMin ( adj curr_path [ level - 1 ]) + firstMin ( adj i )) / 2 ; } // curr_bound + curr_weight is the actual lower bound // for the node that we have arrived on // If current lower bound < final_res we need to explore // the node further if ( curr_bound + curr_weight < final_res ){ curr_path [ level ] = i ; visited [ i ] = true ; // call TSPRec for the next level TSPRec ( adj curr_bound curr_weight level + 1 curr_path ); } // Else we have to prune the node by resetting // all changes to curr_weight and curr_bound curr_weight -= adj [ curr_path [ level - 1 ]][ i ]; curr_bound = temp ; // Also reset the visited array visited . fill ( false ) for ( var j = 0 ; j <= level - 1 ; j ++ ) visited [ curr_path [ j ]] = true ; } } } // This function sets up final_path[] function TSP ( adj ) { let curr_path = Array ( N + 1 ). fill ( - 1 ); // Calculate initial lower bound for the root node // using the formula 1/2 * (sum of first min + // second min) for all edges. // Also initialize the curr_path and visited array let curr_bound = 0 ; visited . fill ( false ); // compute initial bound for ( let i = 0 ; i < N ; i ++ ){ curr_bound += firstMin ( adj i ) + secondMin ( adj i ); } // Rounding off the lower bound to an integer curr_bound = curr_bound == 1 ? ( curr_bound / 2 ) + 1 : ( curr_bound / 2 ); // We start at vertex 1 so the first vertex // in curr_path[] is 0 visited [ 0 ] = true ; curr_path [ 0 ] = 0 ; // Call to TSPRec for curr_weight equal to // 0 and level 1 TSPRec ( adj curr_bound 0 1 curr_path ); } //Adjacency matrix for the given graph let adj = [[ 0 10 15 20 ] [ 10 0 35 25 ] [ 15 35 0 30 ] [ 20 25 30 0 ]]; TSP ( adj ); console . log ( `Minimum cost: ${ final_res } ` ); console . log ( `Path Taken: ${ final_path . join ( ' ' ) } ` ); // This code is contributed by anskalyan3.
출력 :
Minimum cost : 80 Path Taken : 0 1 3 2 0
반올림은이 코드 라인에서 수행되고 있습니다.
if (level==1) curr_bound -= ((firstMin(adj curr_path[level-1]) + firstMin(adj i))/2); else curr_bound -= ((secondMin(adj curr_path[level-1]) + firstMin(adj i))/2);
분기 및 바인딩 TSP 알고리즘에서는 각 정점의 최소 에지 비용을 추가 한 다음 2로 나누어 최적 솔루션의 총 비용에 대한 하한을 계산합니다. 그러나이 하한은 정수가 아닐 수 있습니다. 정수 하부를 얻으려면 반올림을 사용할 수 있습니다.
위의 코드에서 Curr_Bound 변수는 최적 솔루션의 총 비용에 대한 현재 하한을 보유합니다. 레벨 레벨에서 새로운 정점을 방문하면 새로운 정점과 가장 가까운 두 이웃의 최소 에지 비용의 합을 취함으로써 새로운 하한 New_bound를 계산합니다. 그런 다음 New_Bound를 가장 가까운 정수로 반올림하여 Curr_Bound 변수를 업데이트합니다.
레벨이 1이면 우리는 가장 가까운 정수로 반올림합니다. 이것은 우리가 지금까지 하나의 정점을 방문했으며 최적 솔루션의 총 비용을 추정하는 데 보수적이기를 원하기 때문입니다. 레벨이 1보다 큰 경우, 우리는 이미 일부 정점을 방문 했으므로 최적 솔루션의 총 비용을보다 정확하게 추정 할 수 있다는 사실을 고려하여보다 공격적인 반올림 전략을 사용합니다.
시간 복잡성 : 분지와 바운드의 최악의 복잡성은 무차별 힘의 복잡성과 명확하게 남아 있습니다. 최악의 경우 우리는 노드를 잘라낼 기회를 얻지 못할 수 있기 때문입니다. 반면 실제로 TSP의 다른 인스턴스에 따라 매우 잘 수행됩니다. 복잡성은 또한 경계 기능의 선택에 달려 있습니다.
참조 :
http://lcm.csa.iisc.ernet.in/dsa/node187.html