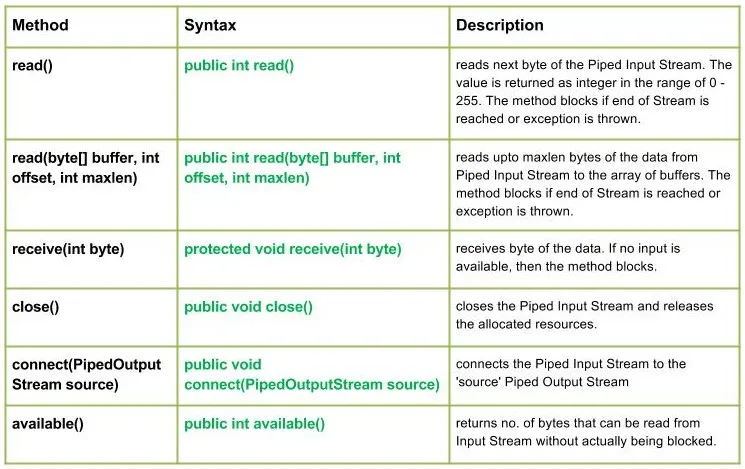
הפוך מערך בקבוצות בגודל נתון


נתון מערך arr[] ומספר שלם ק מצא את המערך לאחר היפוך של כל תת-מערך של k אלמנטים עוקבים במקום. אם במערך המשנה האחרון יש פחות מ-k אלמנטים, הפוך אותו כפי שהוא. שנה את המערך במקום אל תחזיר כלום.
דוגמאות:
קֶלֶט: arr[] = [1 2 3 4 5 6 7 8] k = 3
תְפוּקָה: [3 2 1 6 5 4 8 7]
הֶסבֵּר: אלמנטים הפוכים: [1 2 3] → [3 2 1] [4 5 6] → [6 5 4] והקבוצה האחרונה [7 8](גודל < 3) is reversed as [8 7].קֶלֶט: arr[] = [1 2 3 4 5] k = 3
פלט: [3 2 1 5 4]
הסבר: הקבוצה הראשונה מורכבת מאלמנטים 1 2 3. הקבוצה השנייה מורכבת מ-4 5.אֲנִי nput: arr[] = [5 6 8 9] k = 5
תְפוּקָה: [9 8 6 5]
הֶסבֵּר: מכיוון ש-k גדול מגודל המערך, המערך כולו הפוך.
[גִישָׁה ] היפוך קבוצה בגודל קבוע
הרעיון הוא לשקול כל תת-מערך בגודל k החל מתחילת המערך ולהפוך אותו. אנחנו צריכים לטפל בכמה מקרים מיוחדים.
=> אם k אינו כפולה של n כאשר n הוא גודל המערך עבור הקבוצה האחרונה יישארו לנו פחות מ-k אלמנטים עלינו להפוך את כל האלמנטים הנותרים.
=> אם k = 1 המערך צריך להישאר ללא שינוי. אם k >= n נהפוך את כל האלמנטים הקיימים במערך.כדי להפוך תת-מערך לשמור על שני מצביעים: שמאל וימין. כעת החליפו את הרכיבים במצביעים שמאלה וימינה והגדלו שמאלה ב-1 והקטנו ימינה ב-1. חזור עד שמצביעים ימינה ושמאלה לא יחצו זה את זה.
עובד:
C++ #include #include using namespace std ; void reverseInGroups ( vector < int >& arr int k ){ // Get the size of the array int n = arr . size (); for ( int i = 0 ; i < n ; i += k ) { int left = i ; // to handle case when k is not multiple of n int right = min ( i + k - 1 n - 1 ); // reverse the sub-array [left right] while ( left < right ) { swap ( arr [ left ++ ] arr [ right -- ]); } } } int main () { vector < int > arr = { 1 2 3 4 5 6 7 8 }; int k = 3 ; reverseInGroups ( arr k ); for ( int num : arr ) cout < < num < < ' ' ; return 0 ; }
C #include void reverseInGroups ( int arr [] int n int k ){ for ( int i = 0 ; i < n ; i += k ) { int left = i ; int right ; // to handle case when k is not multiple // of n if ( i + k -1 < n -1 ) right = i + k -1 ; else right = n -1 ; // reverse the sub-array [left right] while ( left < right ) { // swap int temp = arr [ left ]; arr [ left ] = arr [ right ]; arr [ right ] = temp ; left ++ ; right -- ; } } } int main () { int arr [] = { 1 2 3 4 5 6 7 8 }; int k = 3 ; int n = sizeof ( arr ) / sizeof ( arr [ 0 ]); reverseInGroups ( arr n k ); for ( int i = 0 ; i < n ; i ++ ) printf ( '%d ' arr [ i ]); return 0 ; }
Java class GfG { static void reverseInGroups ( int [] arr int k ){ int n = arr . length ; for ( int i = 0 ; i < n ; i += k ) { int left = i ; int right = Math . min ( i + k - 1 n - 1 ); // reverse the sub-array while ( left < right ) { int temp = arr [ left ] ; arr [ left ] = arr [ right ] ; arr [ right ] = temp ; left ++ ; right -- ; } } } public static void main ( String [] args ) { int [] arr = { 1 2 3 4 5 6 7 8 }; int k = 3 ; reverseInGroups ( arr k ); for ( int num : arr ) { System . out . print ( num + ' ' ); } } }
Python def reverseInGroups ( arr k ): i = 0 # get the size of the array n = len ( arr ) while i < n : left = i # To handle case when k is not # multiple of n right = min ( i + k - 1 n - 1 ) # reverse the sub-array [left right] while left < right : arr [ left ] arr [ right ] = arr [ right ] arr [ left ] left += 1 right -= 1 i += k if __name__ == '__main__' : arr = [ 1 2 3 4 5 6 7 8 ] k = 3 reverseInGroups ( arr k ) print ( ' ' . join ( map ( str arr )))
C# using System ; class GfG { public static void reverseInGroups ( int [] arr int k ){ int n = arr . Length ; for ( int i = 0 ; i < n ; i += k ) { int left = i ; // to handle case when k is // not multiple of n int right = Math . Min ( i + k - 1 n - 1 ); int temp ; // reverse the sub-array [left right] while ( left < right ) { temp = arr [ left ]; arr [ left ] = arr [ right ]; arr [ right ] = temp ; left += 1 ; right -= 1 ; } } } public static void Main ( string [] args ){ int [] arr = new int [] { 1 2 3 4 5 6 7 8 }; int k = 3 ; int n = arr . Length ; reverseInGroups ( arr k ); for ( int i = 0 ; i < n ; i ++ ) { Console . Write ( arr [ i ] + ' ' ); } } }
JavaScript function reverseInGroups ( arr k ) { let n = arr . length ; for ( let i = 0 ; i < n ; i += k ) { let left = i ; // to handle case when k is not // multiple of n let right = Math . min ( i + k - 1 n - 1 ); // reverse the sub-array [left right] while ( left < right ) { // Swap elements [ arr [ left ] arr [ right ]] = [ arr [ right ] arr [ left ]]; left += 1 ; right -= 1 ; } } return arr ; } // Driver Code let arr = [ 1 2 3 4 5 6 7 8 ]; let k = 3 ; let arr1 = reverseInGroups ( arr k ); console . log ( arr1 . join ( ' ' ));
תְפוּקָה
3 2 1 6 5 4 8 7
מורכבות זמן: O(n) אנחנו עוברים על כל המערך רק פעם אחת והופכים אלמנטים בקבוצות בגודל k. מכיוון שאיננו חוזרים על אף אלמנט, סך כל העבודה שבוצעה גדל באופן ליניארי עם גודל המערך. אז אם למערך יש n אלמנטים הוא לוקח בערך n צעדים.
מרחב עזר: O(1) ההיפוך נעשה ישירות בתוך המערך המקורי תוך שימוש בכמה משתנים נוספים בלבד.