ALGORITMO LUHN - TECHCODEVIEW.COM

L'algoritmo di Luhn, noto anche come modulo 10 O verso le 10 algoritmo, è una semplice formula di checksum utilizzata per convalidare una varietà di numeri di identificazione, come numeri di carta di credito, numeri IMEI e numeri di previdenza sociale canadesi. La formula LUHN è stata creata alla fine degli anni '60 da un gruppo di matematici. Poco dopo lo adottarono le società di carte di credito. Poiché l’algoritmo è di dominio pubblico, può essere utilizzato da chiunque. La maggior parte delle carte di credito e molti numeri di identificazione governativa utilizzano l'algoritmo come un metodo semplice per distinguere i numeri validi da quelli digitati erroneamente o altrimenti errati. È stato progettato per proteggere da errori accidentali e non da attacchi dannosi.

Passi coinvolti nell'algoritmo di Luhn

Capiamo l'algoritmo con un esempio:
Considera l'esempio di un numero di conto 79927398713 .

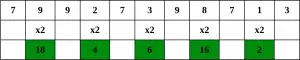
Passo 1 – Partendo dalla cifra più a destra, raddoppia il valore di ogni seconda cifra,

Passo 2 – Se il raddoppio di un numero dà come risultato un numero di due cifre, ovvero maggiore di 9 (ad esempio, 6 × 2 = 12), quindi sommare le cifre del prodotto (ad esempio, 12: 1 + 2 = 3, 15: 1 + 5 = 6), per ottenere un numero a una cifra.

Passaggio 3 – Ora prendi la somma di tutte le cifre.

Passaggio 4 – Se il totale modulo 10 è uguale a 0 (se il totale termina con zero) allora il numero è valido secondo la formula di Luhn; altrimenti non è valido.

Poiché la somma è 70, ovvero un multiplo di 10, è possibile che il numero di conto sia valido.

L'idea è semplice; attraversiamo dalla fine. Per ogni seconda cifra, la raddoppiamo prima di aggiungerla. Aggiungiamo due cifre del numero ottenuto dopo il raddoppio.

Implementazione:

C++

// C++ program to implement Luhn algorithm> #include> using> namespace> std;> // Returns true if given card number is valid> bool> checkLuhn(> const> string& cardNo)> {> > int> nDigits = cardNo.length();> > int> nSum = 0, isSecond => false> ;> > for> (> int> i = nDigits - 1; i>= 0; i--) {> > int> d = cardNo[i] -> '0'> ;> > if> (isSecond ==> true> )> > d = d * 2;> > // We add two digits to handle> > // cases that make two digits after> > // doubling> > nSum += d / 10;> > nSum += d % 10;> > isSecond = !isSecond;> > }> > return> (nSum % 10 == 0);> }> // Driver code> int> main()> {> > string cardNo => '79927398713'> ;> > if> (checkLuhn(cardNo))> > printf> (> 'This is a valid card'> );> > else> > printf> (> 'This is not a valid card'> );> > return> 0;> }>

Giava

// Java program to implement> // Luhn algorithm> import> java.io.*;> class> GFG {> > // Returns true if given> // card number is valid> static> boolean> checkLuhn(String cardNo)> {> > int> nDigits = cardNo.length();> > int> nSum => 0> ;> > boolean> isSecond => false> ;> > for> (> int> i = nDigits -> 1> ; i>=> 0> ; i--)> > {> > int> d = cardNo.charAt(i) -> '0'> ;> > if> (isSecond ==> true> )> > d = d *> 2> ;> > // We add two digits to handle> > // cases that make two digits> > // after doubling> > nSum += d /> 10> ;> > nSum += d %> 10> ;> > isSecond = !isSecond;> > }> > return> (nSum %> 10> ==> 0> );> }> > // Driver code> > static> public> void> main (String[] args)> > {> > String cardNo => '79927398713'> ;> > if> (checkLuhn(cardNo))> > System.out.println(> 'This is a valid card'> );> > else> > System.out.println(> 'This is not a valid card'> );> > > }> }> // This Code is contributed by vt_m.>

Python3

# Python3 program to implement> # Luhn algorithm> # Returns true if given card> # number is valid> def> checkLuhn(cardNo):> > > nDigits> => len> (cardNo)> > nSum> => 0> > isSecond> => False> > > for> i> in> range> (nDigits> -> 1> ,> -> 1> ,> -> 1> ):> > d> => ord> (cardNo[i])> -> ord> (> '0'> )> > > if> (isSecond> => => True> ):> > d> => d> *> 2> > > # We add two digits to handle> > # cases that make two digits after> > # doubling> > nSum> +> => d> /> /> 10> > nSum> +> => d> %> 10> > > isSecond> => not> isSecond> > > if> (nSum> %> 10> => => 0> ):> > return> True> > else> :> > return> False> # Driver code> if> __name__> => => '__main__'> :> > > cardNo> => '79927398713'> > > if> (checkLuhn(cardNo)):> > print> (> 'This is a valid card'> )> > else> :> > print> (> 'This is not a valid card'> )> # This code is contributed by rutvik_56>

C#

// C# program to implement> // Luhn algorithm> using> System;> class> GFG {> > // Returns true if given> // card number is valid> static> bool> checkLuhn(String cardNo)> {> > int> nDigits = cardNo.Length;> > int> nSum = 0;> > bool> isSecond => false> ;> > for> (> int> i = nDigits - 1; i>= 0; i--)> > {> > int> d = cardNo[i] -> '0'> ;> > if> (isSecond ==> true> )> > d = d * 2;> > // We add two digits to handle> > // cases that make two digits> > // after doubling> > nSum += d / 10;> > nSum += d % 10;> > isSecond = !isSecond;> > }> > return> (nSum % 10 == 0);> }> > // Driver code> > static> public> void> Main()> > {> > String cardNo => '79927398713'> ;> > if> (checkLuhn(cardNo))> > Console.WriteLine(> 'This is a valid card'> );> > else> > Console.WriteLine(> 'This is not a valid card'> );> > > }> }> // This Code is contributed by vt_m.>

Javascript

> > // Javascript program to implement Luhn algorithm> > > // Returns true if given> > // card number is valid> > function> checkLuhn(cardNo)> > {> > let nDigits = cardNo.length;> > let nSum = 0;> > let isSecond => false> ;> > for> (let i = nDigits - 1; i>= 0; i--)> > {> > let d = cardNo[i].charCodeAt() -> '0'> .charCodeAt();> > if> (isSecond ==> true> )> > d = d * 2;> > // We add two digits to handle> > // cases that make two digits> > // after doubling> > nSum += parseInt(d / 10, 10);> > nSum += d % 10;> > isSecond = !isSecond;> > }> > return> (nSum % 10 == 0);> > }> > > let cardNo => '79927398713'> ;> > if> (checkLuhn(cardNo))> > document.write(> 'This is a valid card'> );> > else> > document.write(> 'This is not a valid card'> );> > >

Produzione