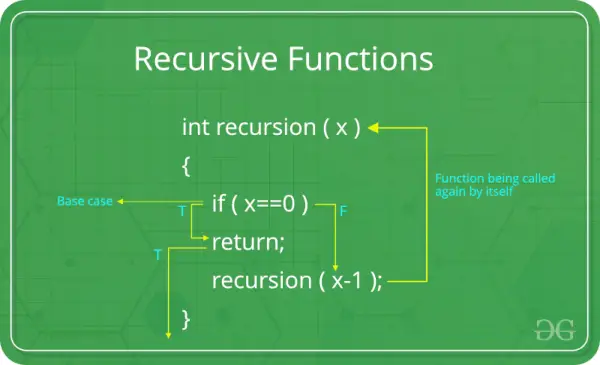
Una funzione ricorsiva può essere definita come una routine che richiama se stessa direttamente o indirettamente.

In altre parole, una funzione ricorsiva è una funzione che risolve un problema risolvendo istanze più piccole dello stesso problema. Questa tecnica è comunemente utilizzata nella programmazione per risolvere problemi che possono essere suddivisi in sottoproblemi più semplici e simili.

Necessità di funzione ricorsiva:

Una funzione ricorsiva è una funzione che risolve un problema risolvendo istanze più piccole dello stesso problema. Questa tecnica viene spesso utilizzata nella programmazione per risolvere problemi che possono essere suddivisi in sottoproblemi più semplici e simili.

1. Risoluzione di compiti complessi:

Le funzioni ricorsive suddividono i problemi complessi in istanze più piccole dello stesso problema, risultando in un codice compatto e leggibile.

2. Dividi e conquista:

Le funzioni ricorsive sono adatte per algoritmi divide et impera come Merge Sort e Quicksort, suddividendo i problemi in sottoproblemi più piccoli, risolvendoli in modo ricorsivo e unendo le soluzioni con il problema originale.

3. Fare marcia indietro :

Il backtracking ricorsivo è l'ideale per esplorare e risolvere problemi come N-Queens e Sudoku.

4. Dinamico programmazione:

Le funzioni ricorsive risolvono in modo efficiente problemi di programmazione dinamica risolvendo sottoproblemi e combinando le loro soluzioni in una soluzione completa.

5. Albero e strutture del grafico:

Le funzioni ricorsive sono ottime per lavorare con strutture ad albero e grafiche, semplificando le attività di attraversamento e riconoscimento di modelli .

Come scrivere una funzione ricorsiva:

Componenti di una funzione ricorsiva:

Caso base: Ogni funzione ricorsiva deve avere un caso base. Il caso base è lo scenario più semplice che non richiede ulteriore ricorsione. Questa è una condizione di terminazione che impedisce alla funzione di richiamarsi indefinitamente. Senza un caso base adeguato, una funzione ricorsiva può portare a una ricorsione infinita.

Caso ricorsivo: Nel caso ricorsivo, la funzione richiama se stessa con gli argomenti modificati. Questa è l’essenza della ricorsione: risolvere un problema più grande scomponendolo in istanze più piccole dello stesso problema. Il caso ricorsivo dovrebbe avvicinarsi al caso base ad ogni iterazione.

Consideriamo l'esempio di fattoriale del numero :

In questo esempio, il caso base è quando N È 0 e la funzione ritorna 1 . Il caso ricorsivo si moltiplica N con il risultato della funzione chiamata con parametro n-1 . Il processo continua fino al raggiungimento del caso base.

È essenziale garantire che la funzione ricorsiva abbia un caso base corretto e che le chiamate ricorsive portino al caso base, altrimenti la procedura potrebbe essere eseguita indefinitamente, portando a un overflow dello stack (superamento della memoria disponibile allocata per le chiamate di funzione).

Di seguito è riportata l'implementazione del fattoriale di un numero:

#include  using namespace std; // Recursive Function to calculate Factorial of a number int factorial(int n) {  // Base case  if (n == 0) {  return 1;  }  // Recursive case  return n * factorial(n - 1); } // Driver Code int main() {  int n = 4;  cout  < < 'Factorial of '  < < n   < < ' is:'  < < factorial(n);  return 0; } 

import java.util.Scanner; public class Factorial {  // Recursive Function to calculate the factorial of a number  static int factorial(int n) {  // Base case: If n is 0, the factorial is 1.  if (n == 0) {  return 1;  }  // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1).  return n * factorial(n - 1);  }  public static void main(String[] args) {  int n = 4;  // Calculate and print the factorial of n.  int result = factorial(n);  System.out.println('Factorial of ' + n + ' is: ' + result);  } } 

# Recursive Function to calculate Factorial of a number def factorial(n): # Base case if n == 0: return 1 # Recursive case return n * factorial(n - 1) # Driver Code if __name__ == '__main__': n = 4 print('Factorial of', n, 'is:', factorial(n)) 

using System; class Program {  // Recursive Function to calculate Factorial of a number  static int Factorial(int n)  {  // Base case  if (n == 0)  {  return 1;  }  // Recursive case  return n * Factorial(n - 1);  }  // Driver Code  static void Main()  {  int n = 4;  Console.WriteLine('Factorial of ' + n + ' is: ' + Factorial(n));  } } 

// Function to calculate the factorial of a number using recursion function factorial(n) {  // Base case: If n is 0, the factorial is 1.  if (n === 0) {  return 1;  }  // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1).  return n * factorial(n - 1); } // Main function function main() {  // Given number  let n = 4;  // Calculate the factorial of n.  let result = factorial(n);  // Print the result  console.log('Factorial of ' + n + ' is: ' + result); } // Call the main function main(); 

Factorial of 4 is:24 

Complessità temporale: SU)
Spazio ausiliario: SU)