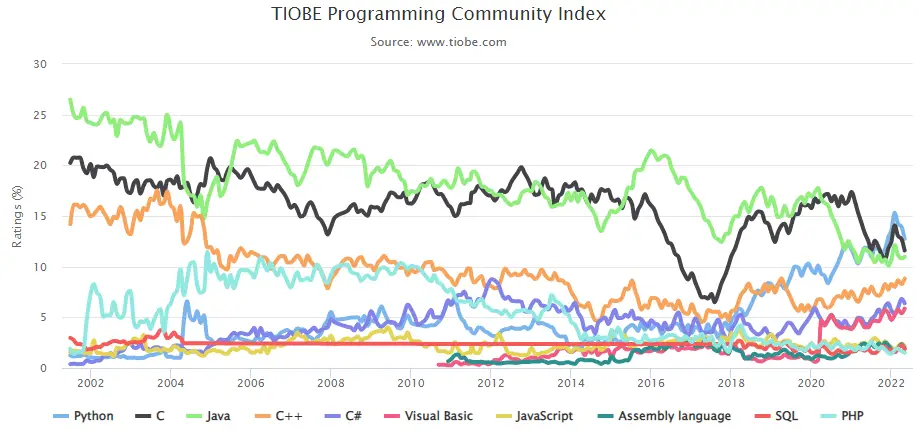
Tasokaavio:

Graafin sanotaan olevan tasomainen, jos se voidaan piirtää tasoon siten, että mikään reuna ei ylitä.
Esimerkki: Kuvassa oleva kaavio on tasokuvaaja.


Kaavion alue: Tarkastellaan tasograafia G=(V,E). Alue määritellään tason alueeksi, jota rajaavat reunat ja jota ei voida jakaa edelleen. Tasokaavio jakaa suunnitelmat yhteen tai useampaan alueeseen. Yksi näistä alueista on ääretön.
Rajallinen alue: Jos alueen pinta-ala on äärellinen, sitä kutsutaan äärelliseksi alueeksi.
Ääretön alue: Jos alueen pinta-ala on ääretön, sitä kutsutaan äärettömäksi alueeksi. Tasograafissa on vain yksi ääretön alue.
Esimerkki: Tarkastellaan kuvan kuvaajaa. Määritä alueiden, äärellisten alueiden ja äärettömän alueen lukumäärä.

Ratkaisu: Yllä olevassa kaaviossa on viisi aluetta, eli r 1 ,r 2 ,r 3 ,r 4 ,r 5 .
Graafissa on neljä äärellistä aluetta, eli r 2 ,r 3 ,r 4 ,r 5 .
On vain yksi äärellinen alue, eli r 1
Tasokaavioiden ominaisuudet:
- Jos yhdistetyllä tasograafilla G on e reunaa ja r aluetta, niin r ≦
 Se on.
Se on. - Jos yhdistetyllä tasograafilla G on e reunaa, v pistettä ja r aluetta, niin v-e+r=2.
- Jos yhdistetyllä tasograafilla G on e reunaa ja v pistettä, niin 3v-e≧6.
- Täydellinen kaavio K n on taso, jos ja vain jos n <5. < li>
- Täydellinen kaksiosainen graafi K mn on tasainen jos ja vain jos m3.
Esimerkki: Todista, että täydellinen graafi K 4 on tasomainen.
Ratkaisu: Täydellinen kaavio K 4 sisältää 4 kärkeä ja 6 reunaa.
Tiedämme, että yhdistetylle tasograafille 3v-e≧6.Siksi K:lle 4 , meillä on 3x4-6=6, joka tyydyttää ominaisuuden (3).
Näin K 4 on tasograafi. Siksi todistettu.
Ei-tasokaavio:
Graafia sanotaan ei-tasomaiseksi, jos sitä ei voida piirtää tasoon siten, että sen reuna ei ylitä.
Esimerkki: Kuvassa esitetyt kaaviot ovat ei-tasomaisia.

Näitä kuvaajia ei voida piirtää tasoon siten, että yksikään reuna ei risteä, joten ne ovat ei-tasograafisia.
Ei-tasokaavioiden ominaisuudet:
Graafi on ei-tasoinen silloin ja vain, jos se sisältää K:lle homeomorfisen osagraafin 5 tai K 3.3
Esimerkki1: Näytä, että K 5 on ei-tasomainen.
Ratkaisu: Täydellinen kaavio K 5 sisältää 5 kärkeä ja 10 reunaa.
Nyt yhdistetylle tasograafille 3v-e≧6.
Siksi K 5 , meillä on 3 x 5-10=5 (joka ei täytä ominaisuutta 3, koska sen on oltava suurempi tai yhtä suuri kuin 6).
Näin ollen K 5 on ei-tasoinen graafi.
Esimerkki2: Osoita, että kuvassa 2 esitetyt kuvaajat ovat ei-tasoisia etsimällä K:n homeomorfinen osagraafi 5 tai K 3.3 .


Ratkaisu: Jos poistamme reunat (V 1 ,SISÄÄN 4 ),(SISÄÄN 3 ,SISÄÄN 4 ) ja (V 5 ,SISÄÄN 4 ) kaavio G 1 , muuttuu K:lle homeomorfiseksi 5 .Siksi se ei ole tasomainen.
Jos poistamme reunan V 2, V 7) kaavio G 2 tulee homeomorfiseksi K:lle 3.3 .Siksi se ei ole tasomainen.
Kaavion väritys:
Oletetaan, että G= (V,E) on graafi, jossa ei ole useita reunoja. G:n kärkiväritys on värien määritys G:n kärkipisteille siten, että vierekkäisillä pisteillä on eri värit. Graafi G on M-värittävä, jos G:lle on olemassa M-värejä käyttävä väritys.
Oikea väritys: Väritys on oikea, jos kahdella vierekkäisellä kärjellä u ja v on eri värit, muuten sitä kutsutaan vääräksi väritykseksi.
Esimerkki: Harkitse seuraavaa kuvaajaa ja väriä C={r, w, b, y}. Väritä kaavio oikein käyttämällä kaikkia värejä tai vähemmän värejä.

Kuvassa esitetty kaavio on vähintään 3-väritettävä, joten x(G)=3
Ratkaisu: Kuvassa on kaavio oikein värjättynä kaikilla neljällä värillä.

Kuvassa on kaavio oikein väritettynä kolmella värillä.

G:n kromaattinen luku: Vähimmäismäärää värejä, jotka tarvitaan graafin G oikean värityksen tuottamiseen, kutsutaan G:n kromaattiseksi lukumääräksi ja sitä merkitään x(G).
Esimerkki: K:n kromaattinen luku n on n.
Ratkaisu: Väritys K n voidaan rakentaa käyttämällä n väriä määrittämällä eri värit jokaiselle kärkipisteelle. Kahdelle pisteelle ei voi antaa samoja värejä, koska tämän graafin jokainen kaksi kärkeä on vierekkäinen. Tästä syystä K:n kromaattinen luku n =n.
Graafisen värityksen sovellukset
Joitakin kaavioiden värityksen sovelluksia ovat:
- Rekisterin allokointi
- Kartan väritys
- Bipartite Graph Checking
- Mobiiliradiotaajuusmääritys
- Aikataulun tekeminen jne.
Esitä ja todista Kättelylause.
Kättelylause: Graafin G kaikkien kärkien asteiden summa on yhtä suuri kuin kaksi kertaa graafin reunojen lukumäärä.
Matemaattisesti se voidaan ilmaista seuraavasti:
∑ v∈V deg(v) = 2e
Todiste: Olkoon G = (V, E) graafi, jossa V = {v 1 ,sisään 2 , . . . . . . . . . .} on pisteiden joukko ja E = {e 1 ,Se on 2 . . . . . . . . . .} on reunojen joukko. Tiedämme, että jokainen reuna on kahden kärjen välissä, joten se antaa kullekin kärjelle yhden asteen. Siten jokainen reuna antaa graafin asteen kaksi. Joten kaikkien pisteiden asteiden summa on yhtä suuri kuin kaksi kertaa G:n reunojen lukumäärä.
Siksi ∑ v∈V deg(v) = 2e