REGRESIÓN LOGÍSTICA EN PROGRAMACIÓN R

La regresión logística en programación R es un algoritmo de clasificación que se utiliza para encontrar la probabilidad de éxito y fracaso de un evento. La regresión logística se utiliza cuando la variable dependiente es de naturaleza binaria (0/1, Verdadero/Falso, Sí/No). La función logit se utiliza como función de enlace en una distribución binomial.

La probabilidad de una variable de resultado binaria se puede predecir utilizando la técnica de modelado estadístico conocida como regresión logística. Se emplea ampliamente en muchas industrias diferentes, incluidas la mercadotecnia, las finanzas, las ciencias sociales y la investigación médica.

La función logística, comúnmente conocida como función sigmoidea, es la idea básica que sustenta la regresión logística. Esta función sigmoidea se utiliza en regresión logística para describir la correlación entre las variables predictivas y la probabilidad del resultado binario.

Regresión logística en programación R

La regresión logística también se conoce como Regresión logística binomial . Se basa en la función sigmoidea donde la salida es probabilidad y la entrada puede ser de -infinito a +infinito.

Teoría

La regresión logística también se conoce como modelo lineal generalizado. Como se utiliza como técnica de clasificación para predecir una respuesta cualitativa, el valor de y varía de 0 a 1 y se puede representar mediante la siguiente ecuación:

Regresión logística en programación R

pag es la probabilidad de la característica de interés. El odds ratio se define como la probabilidad de éxito en comparación con la probabilidad de fracaso. Es una representación clave de los coeficientes de regresión logística y puede tomar valores entre 0 e infinito. El odds ratio de 1 es cuando la probabilidad de éxito es igual a la probabilidad de fracaso. El odds ratio de 2 es cuando la probabilidad de éxito es el doble de la probabilidad de fracaso. El odds ratio de 0,5 es cuando la probabilidad de fracaso es el doble de la probabilidad de éxito.

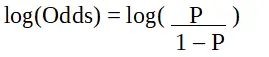
Regresión logística en programación R

Dado que estamos trabajando con una distribución binomial (variable dependiente), debemos elegir la función de enlace que mejor se adapte a esta distribución.

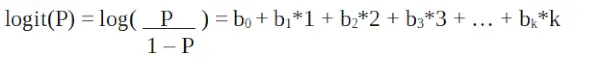
Regresión logística en programación R

Es un función logit . En la ecuación anterior, el paréntesis se elige para maximizar la probabilidad de observar los valores de la muestra en lugar de minimizar la suma de errores cuadrados (como la regresión ordinaria). El logit también se conoce como registro de probabilidades. La función logit debe estar relacionada linealmente con las variables independientes. Esto es de la ecuación A, donde el lado izquierdo es una combinación lineal de x. Esto es similar al supuesto de MCO de que y está relacionado linealmente con x. Las variables b0, b1, b2… etc. son desconocidas y deben estimarse a partir de los datos de entrenamiento disponibles. En un modelo de regresión logística, multiplicar b1 por una unidad cambia el logit por b0. Los cambios de P debido a un cambio de una unidad dependerán del valor multiplicado. Si b1 es positivo entonces P aumentará y si b1 es negativo entonces P disminuirá.

El conjunto de datos

mtcars (Prueba en carretera de automóviles de tendencia de motor) comprende el consumo de combustible, el rendimiento y 10 aspectos del diseño del automóvil para 32 automóviles. Viene preinstalado con dplyr paquete en R.

R

# Installing the package> install.packages> (> 'dplyr'> )> # Loading package> library> (dplyr)> # Summary of dataset in package> summary> (mtcars)>

Realizar una regresión logística en un conjunto de datos

La regresión logística se implementa en R usando glm() entrenando el modelo utilizando características o variables en el conjunto de datos.

R

# Installing the package> # For Logistic regression> install.packages> (> 'caTools'> )> # For ROC curve to evaluate model> install.packages> (> 'ROCR'> )> > # Loading package> library> (caTools)> library> (ROCR)>

Dividiendo los datos

R

# Splitting dataset> split <-> sample.split> (mtcars, SplitRatio = 0.8)> split> train_reg <-> subset> (mtcars, split ==> 'TRUE'> )> test_reg <-> subset> (mtcars, split ==> 'FALSE'> )> # Training model> logistic_model <-> glm> (vs ~ wt + disp,> > data = train_reg,> > family => 'binomial'> )> logistic_model> # Summary> summary> (logistic_model)>

Producción:

Call: glm(formula = vs ~ wt + disp, family = 'binomial', data = train_reg) Deviance Residuals: Min 1Q Median 3Q Max -1.6552 -0.4051 0.4446 0.6180 1.9191 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercepción) 1,58781 2,60087 0,610 0,5415 peso 1,36958 1,60524 0,853 0,3936 disp -0,02969 0,01577 -1,882 0,0598 . --- Significativo. códigos: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1 (el parámetro de dispersión para la familia binomial se considera 1) Desviación nula: 34,617 en 24 grados de libertad Desviación residual: 20,212 en 22 grados de libertad AIC: 26.212 Número de iteraciones de puntuación de Fisher: 6

Llamada: se muestra la llamada a la función utilizada para ajustar el modelo de regresión logística, junto con información sobre la familia, la fórmula y los datos. Residuos de desviación: estos son los residuos de desviación, que miden el grado de bondad de ajuste del modelo. Representan discrepancias entre las respuestas reales y la probabilidad predicha por el modelo de regresión logística. Coeficientes: estos coeficientes en la regresión logística representan las probabilidades logarítmicas o logit de la variable de respuesta. Los errores estándar relacionados con los coeficientes estimados se muestran en el estándar. Columna de errores. Códigos de significancia: el nivel de significancia de cada variable predictiva se indica mediante los códigos de significancia. Parámetro de dispersión: en la regresión logística, el parámetro de dispersión sirve como parámetro de escala para la distribución binomial. En este caso, se establece en 1, lo que indica que la dispersión supuesta es 1. Desviación nula: la desviación nula calcula la desviación del modelo cuando solo se tiene en cuenta la intersección. Simboliza la desviación que resultaría de un modelo sin predictores. Desviación residual: la desviación residual calcula la desviación del modelo después de que se hayan ajustado los predictores. Representa la desviación residual después de tener en cuenta los predictores. AIC: El Criterio de Información de Akaike (AIC), que tiene en cuenta el número de predictores, es un indicador de la bondad de ajuste de un modelo. Penaliza los modelos más complejos para evitar el sobreajuste. Los modelos que se ajustan mejor se indican con valores de AIC más bajos. Número de iteraciones de puntuación de Fisher: el número de iteraciones que necesita el procedimiento de puntuación de Fisher para estimar los parámetros del modelo se indica mediante el número de iteraciones.

Predecir datos de prueba basados en el modelo

R

predict_reg <-> predict> (logistic_model,> > test_reg, type => 'response'> )> predict_reg>

Producción:

Hornet Sportabout Merc 280C Merc 450SE Chrysler Imperial 0.01226166 0.78972164 0.26380531 0.01544309 AMC Javelin Camaro Z28 Ford Pantera L 0.06104267 0.02807992 0.01107943

R

# Changing probabilities> predict_reg <-> ifelse> (predict_reg>0.5, 1, 0)> # Evaluating model accuracy> # using confusion matrix> table> (test_reg$vs, predict_reg)> missing_classerr <-> mean> (predict_reg != test_reg$vs)> print> (> paste> (> 'Accuracy ='> , 1 - missing_classerr))> # ROC-AUC Curve> ROCPred <-> prediction> (predict_reg, test_reg$vs)> ROCPer <-> performance> (ROCPred, measure => 'tpr'> ,> > x.measure => 'fpr'> )> auc <-> performance> (ROCPred, measure => 'auc'> )> auc <- [email protected][[1]]> auc> # Plotting curve> plot> (ROCPer)> plot> (ROCPer, colorize => TRUE> ,> > print.cutoffs.at => seq> (0.1, by = 0.1),> > main => 'ROC CURVE'> )> abline> (a = 0, b = 1)> auc <-> round> (auc, 4)> legend> (.6, .4, auc, title => 'AUC'> , cex = 1)>

Producción:

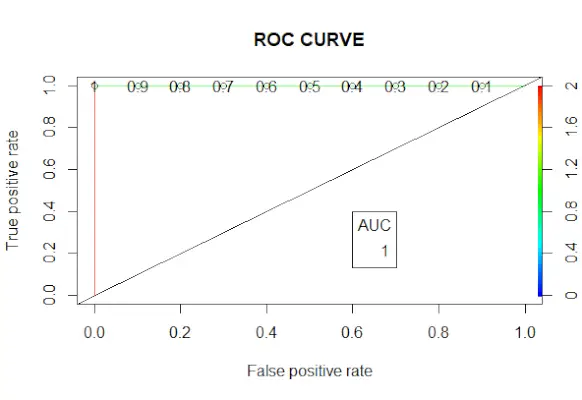
Curva ROC

Ejemplo 2:

Podemos realizar un modelo de regresión logística Titanic Data establecido en R.

R

# Load the dataset> data> (Titanic)> # Convert the table to a data frame> data <-> as.data.frame> (Titanic)> # Fit the logistic regression model> model <-> glm> (Survived ~ Class + Sex + Age, family = binomial, data = data)> # View the summary of the model> summary> (model)>

Producción:

Call: glm(formula = Survived ~ Class + Sex + Age, family = binomial, data = data) Deviance Residuals: Min 1Q Median 3Q Max -1.177 -1.177 0.000 1.177 1.177 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercepción) 4.022e-16 8.660e-01 0 1 Clase2nd -9.762e-16 1.000e+00 0 1 Class3rd -4.699e-16 1.000e+00 0 1 ClassCrew -5.551e-16 1.000e+ 00 0 1 SexoMujer -3.140e-16 7.071e-01 0 1 EdadAdulto 5.103e-16 7.071e-01 0 1 (Parámetro de dispersión para familia binomial tomado como 1) Desviación nula: 44.361 en 31 grados de libertad Desviación residual: 44.361 en 26 grados de libertad AIC: 56.361 Número de iteraciones de puntuación de Fisher: 2

Trazar la curva ROC para el conjunto de datos del Titanic

R

# Install and load the required packages> install.packages> (> 'ROCR'> )> library> (ROCR)> # Fit the logistic regression model> model <-> glm> (Survived ~ Class + Sex + Age, family = binomial, data = data)> # Make predictions on the dataset> predictions <-> predict> (model, type => 'response'> )> # Create a prediction object for ROCR> prediction_objects <-> prediction> (predictions, titanic_df$Survived)> # Create an ROC curve object> roc_object <-> performance> (prediction_obj, measure => 'tpr'> , x.measure => 'fpr'> )> # Plot the ROC curve> plot> (roc_object, main => 'ROC Curve'> , col => 'blue'> , lwd = 2)> # Add labels and a legend to the plot> legend> (> 'bottomright'> , legend => > paste> (> 'AUC ='> ,> round> (> performance> (prediction_objects, measure => 'auc'> )> > @y.values[[1]], 2)), col => 'blue'> , lwd = 2)>

Producción:

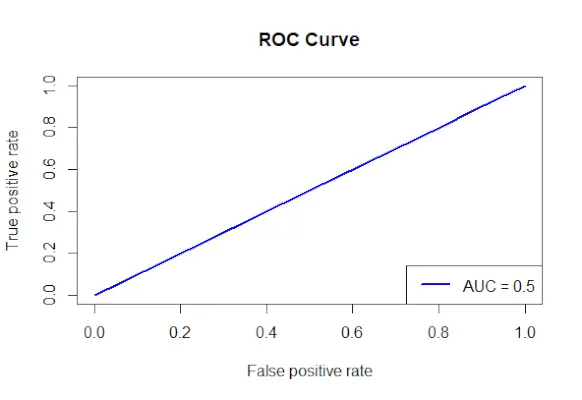
curva ROC

Se especifican los factores utilizados para predecir los supervivientes y se utiliza la fórmula Clase de supervivientes + Sexo + Edad para crear un modelo de regresión logística.
Utilizando la función predict(), se realizan predicciones en el conjunto de datos utilizando el modelo ajustado.
Las probabilidades proyectadas se combinan con los valores de resultado reales para crear un objeto de predicción utilizando el método predict() del paquete ROCR.
Se especifican la medida de la tasa de verdaderos positivos (tpr) y la medida del eje x de la tasa de falsos positivos (fpr), y se crea un objeto de curva ROC utilizando la función performance() del paquete ROCR.
El objeto de curva ROC (roc_obj), que especifica el título principal, el color y el ancho de la línea, se traza utilizando la función plot().
Utiliza la función performance() con medida = auc para determinar el valor de AUC (área bajo la curva) y agrega etiquetas y una leyenda al gráfico.