Algoritmo de multiplicación de Booth

El algoritmo de stand es un algoritmo de multiplicación que nos permite multiplicar los dos enteros binarios con signo en complemento a 2, respectivamente. También se utiliza para acelerar la realización del proceso de multiplicación. También es muy eficiente. Funciona con los bits de cadena 0 en el multiplicador, lo que no requiere ningún bit adicional, solo desplaza los bits de cadena más a la derecha y una cadena de unos en un peso de bit multiplicador de 2. k al peso 2 metro que se puede considerar como 2 k+ 1 - 2 metro .
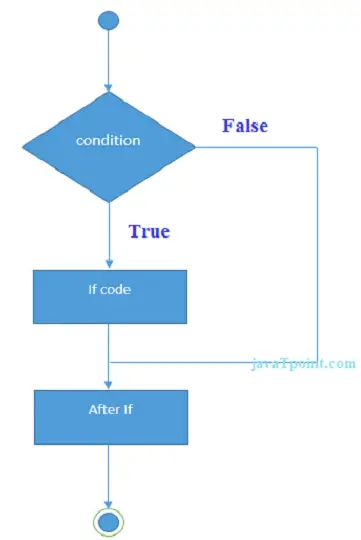
A continuación se muestra la representación gráfica del algoritmo de Booth:

En el diagrama de flujo anterior, inicialmente, C.A. y q norte + 1 Los bits se establecen en 0 y el CAROLINA DEL SUR es un contador de secuencia que representa el conjunto total de bits norte, que es igual al número de bits en el multiplicador. Hay BR que representan el bits multiplicando, y QR representa el bits multiplicadores . Después de eso, encontramos dos bits del multiplicador como Q norte y q norte + 1 , donde Qn representa el último bit de QR y Q norte + 1 representa el bit incrementado de Qn en 1. Supongamos que dos bits del multiplicador son iguales a 10; significa que tenemos que restar el multiplicador del producto parcial en el acumulador AC y luego realizar la operación de desplazamiento aritmético (ashr). Si los dos multiplicadores son iguales a 01, significa que debemos realizar la suma del multiplicando al producto parcial en el acumulador AC y luego realizar la operación de desplazamiento aritmético ( ashr ), incluido q norte + 1 . La operación de desplazamiento aritmético se utiliza en el algoritmo de Booth para desplazar los bits AC y QR uno a la derecha y mantiene el bit de signo en AC sin cambios. Y el contador de secuencia disminuye continuamente hasta que se repite el ciclo computacional, igual al número de bits (n).
Trabajando en el algoritmo de stand
- Establezca los bits binarios Multiplicando y Multiplicador como M y Q, respectivamente.
- Inicialmente, configuramos AC y Q norte + 1 registra el valor a 0.
- SC representa el número de bits multiplicadores (Q) y es un contador de secuencia que disminuye continuamente hasta igualar el número de bits (n) o llegar a 0.
- Un Qn representa el último bit de Q, y el Q n+1 muestra el bit incrementado de Qn en 1.
- En cada ciclo del algoritmo de cabina, Q norte y q norte + 1 Los bits se verificarán en los siguientes parámetros de la siguiente manera:
- Cuando dos bits Q norte y q norte + 1 son 00 u 11, simplemente realizamos la operación de desplazamiento aritmético a la derecha (ashr) al producto parcial AC. Y los bits de Qn y Q norte + 1 se incrementa en 1 bit.
- Si los bits de Q norte y q norte + 1 Si muestra 01, los bits del multiplicando (M) se agregarán al AC (registro del acumulador). Después de eso, realizamos la operación de desplazamiento a la derecha a los bits AC y QR en 1.
- Si los bits de Q norte y q norte + 1 Si muestra 10, los bits del multiplicando (M) se restarán del AC (registro del acumulador). Después de eso, realizamos la operación de desplazamiento a la derecha a los bits AC y QR en 1.
- La operación funciona continuamente hasta que alcanzamos n - 1 bit en el algoritmo de cabina.
- Los resultados de los bits binarios de multiplicación se almacenarán en los registros AC y QR.
Hay dos métodos utilizados en el algoritmo de Booth:
1. RSC (Circular de desplazamiento a la derecha)
Desplaza el bit más a la derecha del número binario y luego se agrega al comienzo de los bits binarios.

2. RSA (aritmética de desplazamiento a la derecha)
Agrega los dos bits binarios y luego desplaza el resultado hacia la derecha una posición de 1 bit.
Ejemplo : 0100 + 0110 => 1010, después de sumar el número binario, desplace cada bit 1 hacia la derecha y coloque el primer bit del resultante al comienzo del nuevo bit.
Ejemplo: multiplica los dos números 7 y 3 usando el algoritmo de multiplicación de Booth.
Años . Aquí tenemos dos números, 7 y 3. En primer lugar, necesitamos convertir 7 y 3 en números binarios como 7 = (0111) y 3 = (0011). Ahora establezca 7 (en binario 0111) como multiplicando (M) y 3 (en binario 0011) como multiplicador (Q). Y SC (Sequence Count) representa el número de bits, y aquí tenemos 4 bits, así que establezca SC = 4. Además, muestra el número de ciclos de iteración de los algoritmos de la cabina y luego los ciclos ejecutados SC = SC - 1 vez.
| q norte | q norte + 1 | M = (0111) M' + 1 = (1001) & Operación | C.A. | q | q norte + 1 | CAROLINA DEL SUR |
|---|---|---|---|---|---|---|
| 1 | 0 | Inicial | 0000 | 0011 | 0 | 4 |
| Sustraer (M'+1) | 1001 | |||||
| 1001 | ||||||
| Realizar operaciones aritméticas de desplazamiento a la derecha (ashr) | 1100 | 1001 | 1 | 3 | ||
| 1 | 1 | Realizar operaciones aritméticas de desplazamiento a la derecha (ashr) | 1110 | 0100 | 1 | 2 |
| 0 | 1 | Suma (A + M) | 0111 | |||
| 0101 | 0100 | |||||
| Realizar operación aritmética de desplazamiento a la derecha | 0010 | 1010 | 0 | 1 | ||
| 0 | 0 | Realizar operación aritmética de desplazamiento a la derecha | 0001 | 0101 | 0 | 0 |
El ejemplo numérico del algoritmo de multiplicación de Booth es 7 x 3 = 21 y la representación binaria de 21 es 10101. Aquí obtenemos el resultado en binario 00010101. Ahora lo convertimos a decimal, como (000010101). 10 = 2*4 + 2*3 + 2*2 + 2*1 + 2*0 => 21.
Ejemplo: multiplica los dos números 23 y -9 usando el algoritmo de multiplicación de Booth.
Aquí, M = 23 = (010111) y Q = -9 = (110111)
| q norte q norte + 1 | METRO = 0 1 0 1 1 1 M' + 1 = 1 0 1 0 0 1 | C.A. | q | q norte + 1 CAROLINA DEL SUR |
|---|---|---|---|---|
| Inicialmente | 000000 | 110111 | 0 6 | |
| 1 0 | Restar M | 101001 | ||
| 101001 | ||||
| Realizar operación aritmética de desplazamiento a la derecha | 110100 | 111011 | 1 5 | |
| 1 1 | Realizar operación aritmética de desplazamiento a la derecha | 111010 | 011101 | 1 4 |
| 1 1 | Realizar operación aritmética de desplazamiento a la derecha | 111101 | 001110 | 1 3 |
| 0 1 | Suma (A + M) | 010111 | ||
| 010100 | ||||
| Realizar operación aritmética de desplazamiento a la derecha | 001010 | 000111 | 0 2 | |
| 1 0 | Restar M | 101001 | ||
| 110011 | ||||
| Realizar operación aritmética de desplazamiento a la derecha | 111001 | 100011 | 1 1 | |
| 1 1 | Realizar operación aritmética de desplazamiento a la derecha | 111100 | 110001 | 1 0 |
q norte + 1 = 1, significa que la salida es negativa.
Por lo tanto, 23 * -9 = complemento a 2 de 111100110001 => (00001100111)