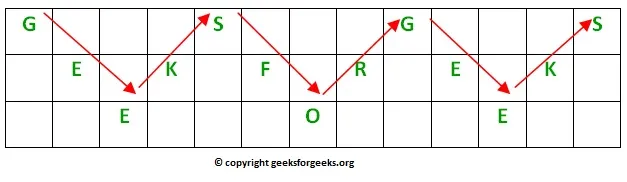
Position eines Elements nach stabiler Sortierung

 #practiceLinkDiv { display: none !important; }
#practiceLinkDiv { display: none !important; } Bei einem Array von Ganzzahlen, das möglicherweise doppelte Elemente enthält, wird uns ein Element dieses Arrays übergeben. Wir müssen die endgültige Position dieses Elements im Array angeben, wenn ein stabiler Sortieralgorithmus angewendet wird.
Beispiele:
Input : arr[] = [3 4 3 5 2 3 4 3 1 5] index = 5 Output : 4 Element initial index – 5 (third 3) After sorting array by stable sorting algorithm we get array as shown below [1(8) 2(4) 3(0) 3(2) 3(5) 3(7) 4(1) 4(6) 5(3) 5(9)] with their initial indices shown in parentheses next to them Element's index after sorting = 4Recommended Practice Stabile Sortierung und Position Probieren Sie es aus!
Eine einfache Möglichkeit, dieses Problem zu lösen, besteht darin, einen beliebigen stabilen Sortieralgorithmus wie zu verwenden Einfügungssortierung Sortieren geht usw. und erhalten dann den neuen Index des angegebenen Elements, aber wir können dieses Problem lösen, ohne das Array zu sortieren.
Da die Position eines Elements in einem sortierten Array nur von den Elementen bestimmt wird, die kleiner als das angegebene Element sind. Wir zählen alle Array-Elemente, die kleiner als das angegebene Element sind, und für diejenigen Elemente, die gleich den angegebenen Elementelementen sind, die vor dem Index des angegebenen Elements auftreten, werden sie in die Anzahl der kleineren Elemente einbezogen, wodurch die Stabilität des Ergebnisindex sichergestellt wird.
Einfacher Code zur Implementierung des oben genannten Ansatzes wird unten implementiert:
C++ // C++ program to get index of array element in // sorted array #include using namespace std ; // Method returns the position of arr[idx] after // performing stable-sort on array int getIndexInSortedArray ( int arr [] int n int idx ) { /* Count of elements smaller than current element plus the equal element occurring before given index*/ int result = 0 ; for ( int i = 0 ; i < n ; i ++ ) { // If element is smaller then increase // the smaller count if ( arr [ i ] < arr [ idx ]) result ++ ; // If element is equal then increase count // only if it occurs before if ( arr [ i ] == arr [ idx ] && i < idx ) result ++ ; } return result ; } // Driver code to test above methods int main () { int arr [] = { 3 4 3 5 2 3 4 3 1 5 }; int n = sizeof ( arr ) / sizeof ( arr [ 0 ]); int idxOfEle = 5 ; cout < < getIndexInSortedArray ( arr n idxOfEle ); return 0 ; }
Java // Java program to get index of array // element in sorted array class ArrayIndex { // Method returns the position of // arr[idx] after performing stable-sort // on array static int getIndexInSortedArray ( int arr [] int n int idx ) { /* Count of elements smaller than current element plus the equal element occurring before given index*/ int result = 0 ; for ( int i = 0 ; i < n ; i ++ ) { // If element is smaller then // increase the smaller count if ( arr [ i ] < arr [ idx ] ) result ++ ; // If element is equal then increase // count only if it occurs before if ( arr [ i ] == arr [ idx ] && i < idx ) result ++ ; } return result ; } // Driver code to test above methods public static void main ( String [] args ) { int arr [] = { 3 4 3 5 2 3 4 3 1 5 }; int n = arr . length ; int idxOfEle = 5 ; System . out . println ( getIndexInSortedArray ( arr n idxOfEle )); } } // This code is contributed by Raghav sharma
Python3 # Python program to get index of array element in # sorted array # Method returns the position of arr[idx] after # performing stable-sort on array def getIndexInSortedArray ( arr n idx ): # Count of elements smaller than current # element plus the equal element occurring # before given index result = 0 for i in range ( n ): # If element is smaller then increase # the smaller count if ( arr [ i ] < arr [ idx ]): result += 1 # If element is equal then increase count # only if it occurs before if ( arr [ i ] == arr [ idx ] and i < idx ): result += 1 return result ; # Driver code to test above methods arr = [ 3 4 3 5 2 3 4 3 1 5 ] n = len ( arr ) idxOfEle = 5 print ( getIndexInSortedArray ( arr n idxOfEle )) # Contributed by: Afzal Ansari
C# // C# program to get index of array // element in sorted array using System ; class ArrayIndex { // Method returns the position of // arr[idx] after performing stable-sort // on array static int getIndexInSortedArray ( int [] arr int n int idx ) { /* Count of elements smaller than current element plus the equal element occurring before given index*/ int result = 0 ; for ( int i = 0 ; i < n ; i ++ ) { // If element is smaller then // increase the smaller count if ( arr [ i ] < arr [ idx ]) result ++ ; // If element is equal then increase // count only if it occurs before if ( arr [ i ] == arr [ idx ] && i < idx ) result ++ ; } return result ; } // Driver code to test above methods public static void Main () { int [] arr = { 3 4 3 5 2 3 4 3 1 5 }; int n = arr . Length ; int idxOfEle = 5 ; Console . WriteLine ( getIndexInSortedArray ( arr n idxOfEle )); } } // This code is contributed by vt_m
PHP // PHP program to get index of // array element in sorted array // Method returns the position of // arr[idx] after performing // stable-sort on array function getIndexInSortedArray ( $arr $n $idx ) { /* Count of elements smaller than current element plus the equal element occurring before given index */ $result = 0 ; for ( $i = 0 ; $i < $n ; $i ++ ) { // If element is smaller then // increase the smaller count if ( $arr [ $i ] < $arr [ $idx ]) $result ++ ; // If element is equal then // increase count only if // it occurs before if ( $arr [ $i ] == $arr [ $idx ] and $i < $idx ) $result ++ ; } return $result ; } // Driver Code $arr = array ( 3 4 3 5 2 3 4 3 1 5 ); $n = count ( $arr ); $idxOfEle = 5 ; echo getIndexInSortedArray ( $arr $n $idxOfEle ); // This code is contributed by anuj_67. ?>
JavaScript < script > // JavaScript program to get index of array // element in sorted array // Method returns the position of // arr[idx] after performing stable-sort // on array function getIndexInSortedArray ( arr n idx ) { /* Count of elements smaller than current element plus the equal element occurring before given index*/ let result = 0 ; for ( let i = 0 ; i < n ; i ++ ) { // If element is smaller then // increase the smaller count if ( arr [ i ] < arr [ idx ]) result ++ ; // If element is equal then increase // count only if it occurs before if ( arr [ i ] == arr [ idx ] && i < idx ) result ++ ; } return result ; } // Driver Code let arr = [ 3 4 3 5 2 3 4 3 1 5 ]; let n = arr . length ; let idxOfEle = 5 ; document . write ( getIndexInSortedArray ( arr n idxOfEle )); // This code is contributed by code_hunt. < /script>
Ausgabe
4
Zeitkomplexität: An) wobei n die Größe des Arrays ist.
Hilfsraum: O(1)
Quiz erstellen