الحد الأدنى لمسار المجموع في صفيف ثلاثي الأبعاد
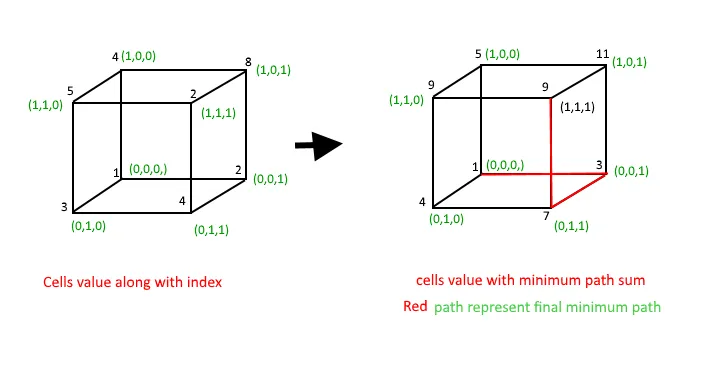
بالنظر إلى مصفوفة ثلاثية الأبعاد arr[l][m][n]، تكون المهمة هي العثور على الحد الأدنى لمجموع المسار من الخلية الأولى في المصفوفة إلى الخلية الأخيرة في المصفوفة. يمكننا فقط العبور إلى العنصر المجاور، أي من خلية معينة (i j k) يمكن اجتياز الخلايا (i+1 j k) (i j+1 k) و(i j k+1) العبور القطري غير مسموح به قد نفترض أن جميع التكاليف هي أعداد صحيحة موجبة.
أمثلة:
Input : arr[][][]= { {{1 2} {3 4}} {{4 8} {5 2}} }; Output : 9 Explanation : arr[0][0][0] + arr[0][0][1] + arr[0][1][1] + arr[1][1][1] Input : { { {1 2} {4 3}} { {3 4} {2 1}} }; Output : 7 Explanation : arr[0][0][0] + arr[0][0][1] + arr[0][1][1] + arr[1][1][1] دعونا نفكر في مصفوفة ثلاثية الأبعاد [2] [2] [2] ممثلة بمكعب مكعب لها قيم على النحو التالي:
arr[][][] = {{{1 2} {3 4}} { {4 8} {5 2}}}; Result = 9 is calculated as: 
هذه المشكلة مشابهة ل الحد الأدنى لمسار التكلفة ويمكن حلها باستخدام البرمجة الديناميكية.
// Array for storing result int tSum[l][m][n]; tSum[0][0][0] = arr[0][0][0]; /* Initialize first row of tSum array */ for (i = 1; i < l; i++) tSum[i][0][0] = tSum[i-1][0][0] + arr[i][0][0]; /* Initialize first column of tSum array */ for (j = 1; j < m; j++) tSum[0][j][0] = tSum[0][j-1][0] + arr[0][j][0]; /* Initialize first width of tSum array */ for (k = 1; k < n; k++) tSum[0][0][k] = tSum[0][0][k-1] + arr[0][0][k]; /* Initialize first row- First column of tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) tSum[i][j][0] = min(tSum[i-1][j][0] tSum[i][j-1][0] INT_MAX) + arr[i][j][0]; /* Initialize first row- First width of tSum array */ for (i = 1; i < l; i++) for (k = 1; k < n; k++) tSum[i][0][k] = min(tSum[i-1][0][k] tSum[i][0][k-1] INT_MAX) + arr[i][0][k]; /* Initialize first width- First column of tSum array */ for (k = 1; k < n; k++) for (j = 1; j < m; j++) tSum[0][j][k] = min(tSum[0][j][k-1] tSum[0][j-1][k] INT_MAX) + arr[0][j][k]; /* Construct rest of the tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) for (k = 1; k < n; k++) tSum[i][j][k] = min(tSum[i-1][j][k] tSum[i][j-1][k] tSum[i][j][k-1]) + arr[i][j][k]; return tSum[l-1][m-1][n-1];C++
// C++ program for Min path sum of 3D-array #include using namespace std ; #define l 3 #define m 3 #define n 3 // A utility function that returns minimum // of 3 integers int min ( int x int y int z ) { return ( x < y ) ? (( x < z ) ? x : z ) : (( y < z ) ? y : z ); } // function to calculate MIN path sum of 3D array int minPathSum ( int arr [][ m ][ n ]) { int i j k ; int tSum [ l ][ m ][ n ]; tSum [ 0 ][ 0 ][ 0 ] = arr [ 0 ][ 0 ][ 0 ]; /* Initialize first row of tSum array */ for ( i = 1 ; i < l ; i ++ ) tSum [ i ][ 0 ][ 0 ] = tSum [ i -1 ][ 0 ][ 0 ] + arr [ i ][ 0 ][ 0 ]; /* Initialize first column of tSum array */ for ( j = 1 ; j < m ; j ++ ) tSum [ 0 ][ j ][ 0 ] = tSum [ 0 ][ j -1 ][ 0 ] + arr [ 0 ][ j ][ 0 ]; /* Initialize first width of tSum array */ for ( k = 1 ; k < n ; k ++ ) tSum [ 0 ][ 0 ][ k ] = tSum [ 0 ][ 0 ][ k -1 ] + arr [ 0 ][ 0 ][ k ]; /* Initialize first row- First column of tSum array */ for ( i = 1 ; i < l ; i ++ ) for ( j = 1 ; j < m ; j ++ ) tSum [ i ][ j ][ 0 ] = min ( tSum [ i -1 ][ j ][ 0 ] tSum [ i ][ j -1 ][ 0 ] INT_MAX ) + arr [ i ][ j ][ 0 ]; /* Initialize first row- First width of tSum array */ for ( i = 1 ; i < l ; i ++ ) for ( k = 1 ; k < n ; k ++ ) tSum [ i ][ 0 ][ k ] = min ( tSum [ i -1 ][ 0 ][ k ] tSum [ i ][ 0 ][ k -1 ] INT_MAX ) + arr [ i ][ 0 ][ k ]; /* Initialize first width- First column of tSum array */ for ( k = 1 ; k < n ; k ++ ) for ( j = 1 ; j < m ; j ++ ) tSum [ 0 ][ j ][ k ] = min ( tSum [ 0 ][ j ][ k -1 ] tSum [ 0 ][ j -1 ][ k ] INT_MAX ) + arr [ 0 ][ j ][ k ]; /* Construct rest of the tSum array */ for ( i = 1 ; i < l ; i ++ ) for ( j = 1 ; j < m ; j ++ ) for ( k = 1 ; k < n ; k ++ ) tSum [ i ][ j ][ k ] = min ( tSum [ i -1 ][ j ][ k ] tSum [ i ][ j -1 ][ k ] tSum [ i ][ j ][ k -1 ]) + arr [ i ][ j ][ k ]; return tSum [ l -1 ][ m -1 ][ n -1 ]; } // Driver program int main () { int arr [ l ][ m ][ n ] = { { { 1 2 4 } { 3 4 5 } { 5 2 1 }} { { 4 8 3 } { 5 2 1 } { 3 4 2 }} { { 2 4 1 } { 3 1 4 } { 6 3 8 }} }; cout < < minPathSum ( arr ); return 0 ; }
Java // Java program for Min path sum of 3D-array import java.io.* ; class GFG { static int l = 3 ; static int m = 3 ; static int n = 3 ; // A utility function that returns minimum // of 3 integers static int min ( int x int y int z ) { return ( x < y ) ? (( x < z ) ? x : z ) : (( y < z ) ? y : z ); } // function to calculate MIN path sum of 3D array static int minPathSum ( int arr [][][] ) { int i j k ; int tSum [][][] = new int [ l ][ m ][ n ] ; tSum [ 0 ][ 0 ][ 0 ] = arr [ 0 ][ 0 ][ 0 ] ; /* Initialize first row of tSum array */ for ( i = 1 ; i < l ; i ++ ) tSum [ i ][ 0 ][ 0 ] = tSum [ i - 1 ][ 0 ][ 0 ] + arr [ i ][ 0 ][ 0 ] ; /* Initialize first column of tSum array */ for ( j = 1 ; j < m ; j ++ ) tSum [ 0 ][ j ][ 0 ] = tSum [ 0 ][ j - 1 ][ 0 ] + arr [ 0 ][ j ][ 0 ] ; /* Initialize first width of tSum array */ for ( k = 1 ; k < n ; k ++ ) tSum [ 0 ][ 0 ][ k ] = tSum [ 0 ][ 0 ][ k - 1 ] + arr [ 0 ][ 0 ][ k ] ; /* Initialize first row- First column of tSum array */ for ( i = 1 ; i < l ; i ++ ) for ( j = 1 ; j < m ; j ++ ) tSum [ i ][ j ][ 0 ] = min ( tSum [ i - 1 ][ j ][ 0 ] tSum [ i ][ j - 1 ][ 0 ] Integer . MAX_VALUE ) + arr [ i ][ j ][ 0 ] ; /* Initialize first row- First width of tSum array */ for ( i = 1 ; i < l ; i ++ ) for ( k = 1 ; k < n ; k ++ ) tSum [ i ][ 0 ][ k ] = min ( tSum [ i - 1 ][ 0 ][ k ] tSum [ i ][ 0 ][ k - 1 ] Integer . MAX_VALUE ) + arr [ i ][ 0 ][ k ] ; /* Initialize first width- First column of tSum array */ for ( k = 1 ; k < n ; k ++ ) for ( j = 1 ; j < m ; j ++ ) tSum [ 0 ][ j ][ k ] = min ( tSum [ 0 ][ j ][ k - 1 ] tSum [ 0 ][ j - 1 ][ k ] Integer . MAX_VALUE ) + arr [ 0 ][ j ][ k ] ; /* Construct rest of the tSum array */ for ( i = 1 ; i < l ; i ++ ) for ( j = 1 ; j < m ; j ++ ) for ( k = 1 ; k < n ; k ++ ) tSum [ i ][ j ][ k ] = min ( tSum [ i - 1 ][ j ][ k ] tSum [ i ][ j - 1 ][ k ] tSum [ i ][ j ][ k - 1 ] ) + arr [ i ][ j ][ k ] ; return tSum [ l - 1 ][ m - 1 ][ n - 1 ] ; } // Driver program public static void main ( String [] args ) { int arr [][][] = { { { 1 2 4 } { 3 4 5 } { 5 2 1 }} { { 4 8 3 } { 5 2 1 } { 3 4 2 }} { { 2 4 1 } { 3 1 4 } { 6 3 8 }} }; System . out . println ( minPathSum ( arr )); } } // This code is contributed by vt_m
Python3 # Python3 program for Min # path sum of 3D-array l = 3 m = 3 n = 3 # A utility function # that returns minimum # of 3 integers def Min ( x y z ): return min ( min ( x y ) z ) # function to calculate MIN # path sum of 3D array def minPathSum ( arr ): tSum = [[[ 0 for k in range ( n )] for j in range ( m )] for i in range ( l )] tSum [ 0 ][ 0 ][ 0 ] = arr [ 0 ][ 0 ][ 0 ] # Initialize first # row of tSum array for i in range ( 1 l ): tSum [ i ][ 0 ][ 0 ] = tSum [ i - 1 ][ 0 ][ 0 ] + arr [ i ][ 0 ][ 0 ] # Initialize first column # of tSum array for j in range ( 1 m ): tSum [ 0 ][ j ][ 0 ] = tSum [ 0 ][ j - 1 ][ 0 ] + arr [ 0 ][ j ][ 0 ] # Initialize first # width of tSum array for k in range ( 1 n ): tSum [ 0 ][ 0 ][ k ] = tSum [ 0 ][ 0 ][ k - 1 ] + arr [ 0 ][ 0 ][ k ] # Initialize first # row- First column of # tSum array for i in range ( 1 l ): for j in range ( 1 m ): tSum [ i ][ j ][ 0 ] = Min ( tSum [ i - 1 ][ j ][ 0 ] tSum [ i ][ j - 1 ][ 0 ] 1000000000 ) + arr [ i ][ j ][ 0 ]; # Initialize first # row- First width of # tSum array for i in range ( 1 l ): for k in range ( 1 n ): tSum [ i ][ 0 ][ k ] = Min ( tSum [ i - 1 ][ 0 ][ k ] tSum [ i ][ 0 ][ k - 1 ] 1000000000 ) + arr [ i ][ 0 ][ k ] # Initialize first # width- First column of # tSum array for k in range ( 1 n ): for j in range ( 1 m ): tSum [ 0 ][ j ][ k ] = Min ( tSum [ 0 ][ j ][ k - 1 ] tSum [ 0 ][ j - 1 ][ k ] 1000000000 ) + arr [ 0 ][ j ][ k ] # Construct rest of # the tSum array for i in range ( 1 l ): for j in range ( 1 m ): for k in range ( 1 n ): tSum [ i ][ j ][ k ] = Min ( tSum [ i - 1 ][ j ][ k ] tSum [ i ][ j - 1 ][ k ] tSum [ i ][ j ][ k - 1 ]) + arr [ i ][ j ][ k ] return tSum [ l - 1 ][ m - 1 ][ n - 1 ] # Driver Code arr = [[[ 1 2 4 ] [ 3 4 5 ] [ 5 2 1 ]] [[ 4 8 3 ] [ 5 2 1 ] [ 3 4 2 ]] [[ 2 4 1 ] [ 3 1 4 ] [ 6 3 8 ]]] print ( minPathSum ( arr )) # This code is contributed by shinjanpatra
C# // C# program for Min // path sum of 3D-array using System ; class GFG { static int l = 3 ; static int m = 3 ; static int n = 3 ; // A utility function // that returns minimum // of 3 integers static int min ( int x int y int z ) { return ( x < y ) ? (( x < z ) ? x : z ) : (( y < z ) ? y : z ); } // function to calculate MIN // path sum of 3D array static int minPathSum ( int [] arr ) { int i j k ; int [ ] tSum = new int [ l m n ]; tSum [ 0 0 0 ] = arr [ 0 0 0 ]; /* Initialize first row of tSum array */ for ( i = 1 ; i < l ; i ++ ) tSum [ i 0 0 ] = tSum [ i - 1 0 0 ] + arr [ i 0 0 ]; /* Initialize first column of tSum array */ for ( j = 1 ; j < m ; j ++ ) tSum [ 0 j 0 ] = tSum [ 0 j - 1 0 ] + arr [ 0 j 0 ]; /* Initialize first width of tSum array */ for ( k = 1 ; k < n ; k ++ ) tSum [ 0 0 k ] = tSum [ 0 0 k - 1 ] + arr [ 0 0 k ]; /* Initialize first row- First column of tSum array */ for ( i = 1 ; i < l ; i ++ ) for ( j = 1 ; j < m ; j ++ ) tSum [ i j 0 ] = min ( tSum [ i - 1 j 0 ] tSum [ i j - 1 0 ] int . MaxValue ) + arr [ i j 0 ]; /* Initialize first row- First width of tSum array */ for ( i = 1 ; i < l ; i ++ ) for ( k = 1 ; k < n ; k ++ ) tSum [ i 0 k ] = min ( tSum [ i - 1 0 k ] tSum [ i 0 k - 1 ] int . MaxValue ) + arr [ i 0 k ]; /* Initialize first width- First column of tSum array */ for ( k = 1 ; k < n ; k ++ ) for ( j = 1 ; j < m ; j ++ ) tSum [ 0 j k ] = min ( tSum [ 0 j k - 1 ] tSum [ 0 j - 1 k ] int . MaxValue ) + arr [ 0 j k ]; /* Construct rest of the tSum array */ for ( i = 1 ; i < l ; i ++ ) for ( j = 1 ; j < m ; j ++ ) for ( k = 1 ; k < n ; k ++ ) tSum [ i j k ] = min ( tSum [ i - 1 j k ] tSum [ i j - 1 k ] tSum [ i j k - 1 ]) + arr [ i j k ]; return tSum [ l - 1 m - 1 n - 1 ]; } // Driver Code static public void Main () { int [ ] arr = {{{ 1 2 4 } { 3 4 5 } { 5 2 1 }} {{ 4 8 3 } { 5 2 1 } { 3 4 2 }} {{ 2 4 1 } { 3 1 4 } { 6 3 8 }}}; Console . WriteLine ( minPathSum ( arr )); } } // This code is contributed by ajit
JavaScript < script > // Javascript program for Min // path sum of 3D-array var l = 3 ; var m = 3 ; var n = 3 ; // A utility function // that returns minimum // of 3 integers function min ( x y z ) { return ( x < y ) ? (( x < z ) ? x : z ) : (( y < z ) ? y : z ); } // function to calculate MIN // path sum of 3D array function minPathSum ( arr ) { var i j k ; var tSum = Array ( l ); for ( var i = 0 ; i < l ; i ++ ) { tSum [ i ] = Array . from ( Array ( m ) ()=> Array ( n )); } tSum [ 0 ][ 0 ][ 0 ] = arr [ 0 ][ 0 ][ 0 ]; /* Initialize first row of tSum array */ for ( i = 1 ; i < l ; i ++ ) tSum [ i ][ 0 ][ 0 ] = tSum [ i - 1 ][ 0 ][ 0 ] + arr [ i ][ 0 ][ 0 ]; /* Initialize first column of tSum array */ for ( j = 1 ; j < m ; j ++ ) tSum [ 0 ][ j ][ 0 ] = tSum [ 0 ][ j - 1 ][ 0 ] + arr [ 0 ][ j ][ 0 ]; /* Initialize first width of tSum array */ for ( k = 1 ; k < n ; k ++ ) tSum [ 0 ][ 0 ][ k ] = tSum [ 0 ][ 0 ][ k - 1 ] + arr [ 0 ][ 0 ][ k ]; /* Initialize first row- First column of tSum array */ for ( i = 1 ; i < l ; i ++ ) for ( j = 1 ; j < m ; j ++ ) tSum [ i ][ j ][ 0 ] = min ( tSum [ i - 1 ][ j ][ 0 ] tSum [ i ][ j - 1 ][ 0 ] 1000000000 ) + arr [ i ][ j ][ 0 ]; /* Initialize first row- First width of tSum array */ for ( i = 1 ; i < l ; i ++ ) for ( k = 1 ; k < n ; k ++ ) tSum [ i ][ 0 ][ k ] = min ( tSum [ i - 1 ][ 0 ][ k ] tSum [ i ][ 0 ][ k - 1 ] 1000000000 ) + arr [ i ][ 0 ][ k ]; /* Initialize first width- First column of tSum array */ for ( k = 1 ; k < n ; k ++ ) for ( j = 1 ; j < m ; j ++ ) tSum [ 0 ][ j ][ k ] = min ( tSum [ 0 ][ j ][ k - 1 ] tSum [ 0 ][ j - 1 ][ k ] 1000000000 ) + arr [ 0 ][ j ][ k ]; /* Construct rest of the tSum array */ for ( i = 1 ; i < l ; i ++ ) for ( j = 1 ; j < m ; j ++ ) for ( k = 1 ; k < n ; k ++ ) tSum [ i ][ j ][ k ] = min ( tSum [ i - 1 ][ j ][ k ] tSum [ i ][ j - 1 ][ k ] tSum [ i ][ j ][ k - 1 ]) + arr [ i ][ j ][ k ]; return tSum [ l - 1 ][ m - 1 ][ n - 1 ]; } // Driver Code var arr = [[[ 1 2 4 ] [ 3 4 5 ] [ 5 2 1 ]] [[ 4 8 3 ] [ 5 2 1 ] [ 3 4 2 ]] [[ 2 4 1 ] [ 3 1 4 ] [ 6 3 8 ]]]; document . write ( minPathSum ( arr )); < /script>
الإخراج:
20
تعقيد الوقت : يا (ل * م * ن)
المساحة المساعدة : يا (ل * م * ن)