Максимізація суми N X N верхньої лівої підматриці із заданої матриці 2N X 2N

Враховуючи а 2N x 2N матриця цілих чисел. Вам дозволено перевертати будь-який рядок або стовпець будь-яку кількість разів і в будь-якому порядку. Завдання полягає в тому, щоб обчислити максимальну суму верхнього лівого N X N підматриця, тобто сума елементів підматриці від (0 0) до (N - 1 N - 1).
приклади:
Вхідні дані: з [][] = {
112 42 83 119
56 125 56 49
15 78 101 43
62 98 114 108
}
Вихід: 414
Дана матриця має розмір 4 X 4, який нам потрібно максимізувати
сума верхньої лівої матриці 2 X 2, тобто
сума mat[0][0] + mat[0][1] + mat[1][0] + mat[1][1].
Наступні операції максимізують суму:
1. Виворітний стовпчик 2
112 42 114 119
56 125 101 49
15 78 56 43
62 98 83 108
2. Виворітний ряд 0
119 114 42 112
56 125 101 49
15 78 56 43
62 98 83 108
Сума лівої верхньої матриці = 119 + 114 + 56 + 125 = 414.
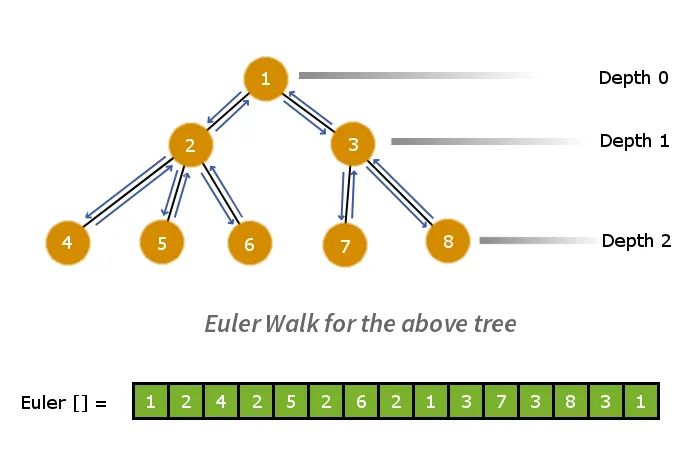
Щоб максимізувати суму верхньої лівої підматриці, спостерігайте, що для кожної комірки верхньої лівої підматриці є чотири кандидати, що означають відповідні комірки у верхній лівій, верхній, правій, нижній лівій та нижній правій підматрицях, якими її можна поміняти місцями.
Тепер спостерігайте за кожною коміркою, де б вона не була, ми можемо поміняти її відповідним значенням-кандидатом у верхній лівій підматриці, не змінюючи порядок інших комірок у верхній лівій підматриці. Діаграма показує приклад, коли максимальне значення з 4 кандидатів знаходиться у верхній правій підматриці. Якщо він знаходиться в нижній лівій або нижній правій підматрицях, ми можемо спочатку змінити рядок або стовпець, щоб помістити їх у верхню праву підматрицю, а потім виконати ту саму послідовність операцій, як показано на схемі.
У цій матриці припустимо a 26 є максимальним із 4 кандидатів і a 23 потрібно замінити на a 26 без зміни порядку комірок у верхній лівій підматриці.

Виворітний ряд 2

Зворотний стовпчик 2

Виворітний ряд 7

Зворотний стовпчик 6

Виворітний ряд 2

Нижче наведено реалізацію цього підходу:
C++ // C++ program to find maximum value of top N/2 x N/2 // matrix using row and column reverse operations #include #define R 4 #define C 4 using namespace std ; int maxSum ( int mat [ R ][ C ]) { int sum = 0 ; for ( int i = 0 ; i < R / 2 ; i ++ ) for ( int j = 0 ; j < C / 2 ; j ++ ) { int r1 = i ; int r2 = R - i - 1 ; int c1 = j ; int c2 = C - j - 1 ; // We can replace current cell [i j] // with 4 cells without changing affecting // other elements. sum += max ( max ( mat [ r1 ][ c1 ] mat [ r1 ][ c2 ]) max ( mat [ r2 ][ c1 ] mat [ r2 ][ c2 ])); } return sum ; } // Driven Program int main () { int mat [ R ][ C ] = { 112 42 83 119 56 125 56 49 15 78 101 43 62 98 114 108 }; cout < < maxSum ( mat ) < < endl ; return 0 ; }
Java // Java program to find maximum value of top N/2 x N/2 // matrix using row and column reverse operations class GFG { static int maxSum ( int mat [][] ) { int sum = 0 ; int maxI = mat . length ; int maxIPossible = maxI - 1 ; int maxJ = mat [ 0 ] . length ; int maxJPossible = maxJ - 1 ; for ( int i = 0 ; i < maxI / 2 ; i ++ ) { for ( int j = 0 ; j < maxJ / 2 ; j ++ ) { // We can replace current cell [i j] // with 4 cells without changing affecting // other elements. sum += Math . max ( Math . max ( mat [ i ][ j ] mat [ maxIPossible - i ][ j ] ) Math . max ( mat [ maxIPossible - i ] [ maxJPossible - j ] mat [ i ][ maxJPossible - j ] )); } } return sum ; } // Driven Program public static void main ( String [] args ) { int mat [][] = { { 112 42 83 119 } { 56 125 56 49 } { 15 78 101 43 } { 62 98 114 108 } }; System . out . println ( maxSum ( mat )); } } /* This Java code is contributed by Rajput-Ji*/
Python3 # Python3 program to find the maximum value # of top N/2 x N/2 matrix using row and # column reverse operations def maxSum ( mat ): Sum = 0 for i in range ( 0 R // 2 ): for j in range ( 0 C // 2 ): r1 r2 = i R - i - 1 c1 c2 = j C - j - 1 # We can replace current cell [i j] # with 4 cells without changing/affecting # other elements. Sum += max ( max ( mat [ r1 ][ c1 ] mat [ r1 ][ c2 ]) max ( mat [ r2 ][ c1 ] mat [ r2 ][ c2 ])) return Sum # Driver Code if __name__ == '__main__' : R = C = 4 mat = [[ 112 42 83 119 ] [ 56 125 56 49 ] [ 15 78 101 43 ] [ 62 98 114 108 ]] print ( maxSum ( mat )) # This code is contributed # by Rituraj Jain
C# // C# program to find maximum value // of top N/2 x N/2 matrix using row // and column reverse operations using System ; class GFG { static int R = 4 ; static int C = 4 ; static int maxSum ( int [ ] mat ) { int sum = 0 ; for ( int i = 0 ; i < R / 2 ; i ++ ) { for ( int j = 0 ; j < C / 2 ; j ++ ) { int r1 = i ; int r2 = R - i - 1 ; int c1 = j ; int c2 = C - j - 1 ; // We can replace current cell [i j] // with 4 cells without changing affecting // other elements. sum += Math . Max ( Math . Max ( mat [ r1 c1 ] mat [ r1 c2 ]) Math . Max ( mat [ r2 c1 ] mat [ r2 c2 ])); } } return sum ; } // Driven Code public static void Main () { int [ ] mat = { { 112 42 83 119 } { 56 125 56 49 } { 15 78 101 43 } { 62 98 114 108 } }; Console . Write ( maxSum ( mat )); } } // This code is contributed // by ChitraNayal
PHP // PHP program to find maximum value // of top N/2 x N/2 matrix using row // and column reverse operations function maxSum ( $mat ) { $R = 4 ; $C = 4 ; $sum = 0 ; for ( $i = 0 ; $i < $R / 2 ; $i ++ ) for ( $j = 0 ; $j < $C / 2 ; $j ++ ) { $r1 = $i ; $r2 = $R - $i - 1 ; $c1 = $j ; $c2 = $C - $j - 1 ; // We can replace current cell [i j] // with 4 cells without changing // affecting other elements. $sum += max ( max ( $mat [ $r1 ][ $c1 ] $mat [ $r1 ][ $c2 ]) max ( $mat [ $r2 ][ $c1 ] $mat [ $r2 ][ $c2 ])); } return $sum ; } // Driver Code $mat = array ( array ( 112 42 83 119 ) array ( 56 125 56 49 ) array ( 15 78 101 43 ) array ( 62 98 114 108 )); echo maxSum ( $mat ) . ' n ' ; // This code is contributed // by Mukul Singh ?>
JavaScript < script > // Javascript program to find maximum value of top N/2 x N/2 // matrix using row and column reverse operations let R = 4 ; let C = 4 ; function maxSum ( mat ) { let sum = 0 ; for ( let i = 0 ; i < R / 2 ; i ++ ) { for ( let j = 0 ; j < C / 2 ; j ++ ) { let r1 = i ; let r2 = R - i - 1 ; let c1 = j ; let c2 = C - j - 1 ; // We can replace current cell [i j] // with 4 cells without changing affecting // other elements. sum += Math . max ( Math . max ( mat [ r1 ][ c1 ] mat [ r1 ][ c2 ]) Math . max ( mat [ r2 ][ c1 ] mat [ r2 ][ c2 ])); } } return sum ; } // Driven Program let mat = [[ 112 42 83 119 ] [ 56 125 56 49 ] [ 15 78 101 43 ] [ 62 98 114 108 ]]; document . write ( maxSum ( mat )); // This code is contributed by avanitrachhadiya2155 < /script>
Вихід
414
Часова складність: O(N 2 ).
Допоміжний простір: O(1) оскільки він використовує постійний простір для змінних
Створіть вікторину