İki Dışbükey Çokgen arasındaki teğetler
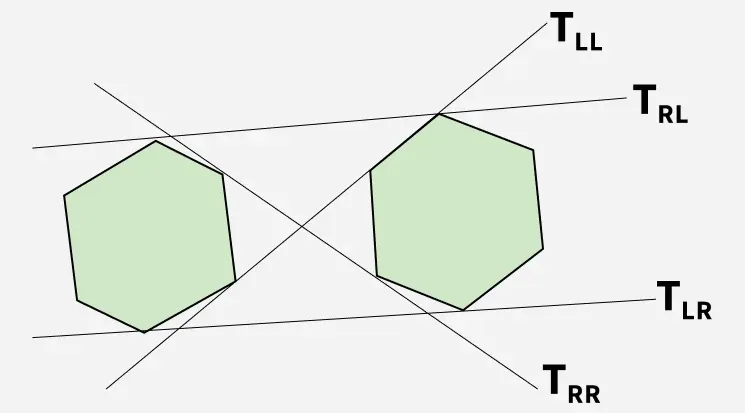
İki dışbükey çokgen verildiğinde, bunları birbirine bağlayan alt ve üst teğetleri belirlemeyi hedefliyoruz.
Aşağıdaki şekilde gösterildiği gibi T RL Ve T LR sırasıyla üst ve alt teğetleri temsil eder.

Örnekler:
Giriş: Birinci Çokgen : [[2 2] [3 3] [5 2] [4 0] [3 1]]
İkinci Çokgen : [[-1 0] [0 1] [1 0] [0 -2]].
Çıkış: Üst Teğet - çizgi birleştirme (01) ve (33)
Alt Teğet - çizgi birleştirme (0-2) ve (40)
Açıklama: Resimde yapı ve iki çokgeni birbirine bağlayan teğetler açıkça görülüyor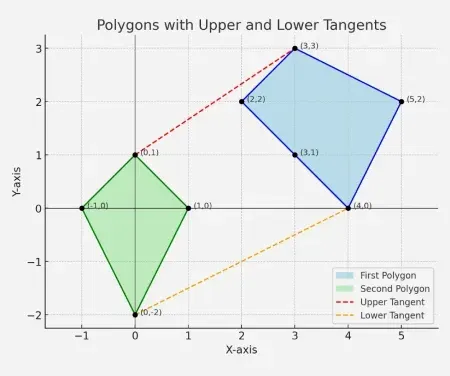
Yaklaşmak:
Üst teğeti bulmak için iki nokta seçerek başlıyoruz: çokgenin en sağ noktası A ve çokgenin en sol noktası B . Bu iki noktayı birleştiren doğruya şu ad verilir: 1. satır . Bu doğru çokgenden geçtiği için B (yani tam üstünde değil) saat yönünün tersine bir sonraki noktaya geçiyoruz B şekillendirme Astar 2 . Bu çizgi artık çokgenin üstünde B bu iyi. Ancak çokgeni geçiyor A bu yüzden bir sonraki noktaya geçiyoruz A saat yönünde oluşturma 3. satır . 3. satır hala çokgeni geçiyor A başka bir hamleye teşvik etmek 4. satır . 4. satır ancak çokgeni geçiyor B o yüzden devam ediyoruz 5. satır . Nihayet 5. satır her iki çokgeni de kesmez, bu da onu verilen çokgenler için doğru üst teğet yapar.
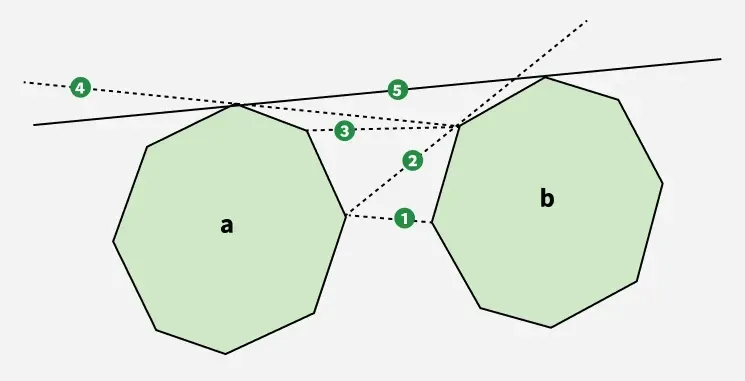
Alttaki teğeti bulmak için çokgenler boyunca ters yönde hareket etmemiz gerekir, yani eğer çizgi b çokgenini geçiyorsa bir sonraki saat yönünde, eğer çizgi a çokgenini geçiyorsa bir sonraki saat yönünün tersine hareket ederiz.
Üst teğet için algoritma:
L ← a'nın en sağ noktası ile b'nin en sol noktasını birleştiren çizgi. while (L çokgenlerden herhangi birini keser) { while(L b'yi keser) L ← L' : b üzerindeki nokta yukarı doğru hareket eder. (L a'yı keserken) L ← L' : a'nın noktası yukarı doğru hareket eder. }
Alt teğet için algoritma:
L ← a'nın en sağ noktası ile b'nin en sol noktasını birleştiren çizgi. while (L çokgenlerden herhangi birini keser) { while (L b'yi keser) L ← L' : b üzerindeki nokta aşağı doğru hareket eder. (L a'yı geçerken) L ← L' : a'nın üzerindeki nokta aşağı doğru hareket eder. }
Yukarıdaki kodun yalnızca üst tanjantı hesapladığını unutmayın. Alt teğeti bulmak için de benzer bir yaklaşım kullanılabilir.
CPP #include using namespace std ; // Determines the quadrant of a point relative to origin int quad ( vector < int > p ) { if ( p [ 0 ] >= 0 && p [ 1 ] >= 0 ) return 1 ; if ( p [ 0 ] <= 0 && p [ 1 ] >= 0 ) return 2 ; if ( p [ 0 ] <= 0 && p [ 1 ] <= 0 ) return 3 ; return 4 ; } // Returns the orientation of ordered triplet (a b c) // 0 -> Collinear 1 -> Clockwise -1 -> Counterclockwise int orientation ( vector < int > a vector < int > b vector < int > c ) { int res = ( b [ 1 ] - a [ 1 ]) * ( c [ 0 ] - b [ 0 ]) - ( c [ 1 ] - b [ 1 ]) * ( b [ 0 ] - a [ 0 ]); if ( res == 0 ) return 0 ; if ( res > 0 ) return 1 ; return -1 ; } // Compare function to sort points counter-clockwise around center bool compare ( vector < int > p1 vector < int > q1 vector < int > mid ) { vector < int > p = { p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ]}; vector < int > q = { q1 [ 0 ] - mid [ 0 ] q1 [ 1 ] - mid [ 1 ]}; int one = quad ( p ); int two = quad ( q ); if ( one != two ) return ( one < two ); return ( p [ 1 ] * q [ 0 ] < q [ 1 ] * p [ 0 ]); } // Sorts the polygon points counter-clockwise vector < vector < int >> sortPoints ( vector < vector < int >> polygon ) { vector < int > mid = { 0 0 }; int n = polygon . size (); // Calculate center (centroid) of the polygon for ( int i = 0 ; i < n ; i ++ ) { mid [ 0 ] += polygon [ i ][ 0 ]; mid [ 1 ] += polygon [ i ][ 1 ]; polygon [ i ][ 0 ] *= n ; polygon [ i ][ 1 ] *= n ; } // Sort points based on their angle from the center sort ( polygon . begin () polygon . end () [ mid ]( vector < int > p1 vector < int > p2 ) { return compare ( p1 p2 mid ); }); // Divide back to original coordinates for ( int i = 0 ; i < n ; i ++ ) { polygon [ i ][ 0 ] /= n ; polygon [ i ][ 1 ] /= n ; } return polygon ; } // Finds the upper tangent between two convex polygons a and b // Returns two points forming the upper tangent vector < vector < int >> findUpperTangent ( vector < vector < int >> a vector < vector < int >> b ) { int n1 = a . size () n2 = b . size (); // Find the rightmost point of polygon a and leftmost point of polygon b int maxa = INT_MIN ; for ( auto & p : a ) maxa = max ( maxa p [ 0 ]); int minb = INT_MAX ; for ( auto & p : b ) minb = min ( minb p [ 0 ]); // Sort both polygons counter-clockwise a = sortPoints ( a ); b = sortPoints ( b ); // Ensure polygon a is to the left of polygon b if ( minb < maxa ) swap ( a b ); n1 = a . size (); n2 = b . size (); // Find the rightmost point in a int ia = 0 ib = 0 ; for ( int i = 1 ; i < n1 ; i ++ ) if ( a [ i ][ 0 ] > a [ ia ][ 0 ]) ia = i ; // Find the leftmost point in b for ( int i = 1 ; i < n2 ; i ++ ) if ( b [ i ][ 0 ] < b [ ib ][ 0 ]) ib = i ; // Initialize starting points int inda = ia indb = ib ; bool done = false ; // Find upper tangent using orientation checks while ( ! done ) { done = true ; // Move to next point in a if necessary while ( orientation ( b [ indb ] a [ inda ] a [( inda + 1 ) % n1 ]) > 0 ) inda = ( inda + 1 ) % n1 ; // Move to previous point in b if necessary while ( orientation ( a [ inda ] b [ indb ] b [( n2 + indb - 1 ) % n2 ]) < 0 ) { indb = ( n2 + indb - 1 ) % n2 ; done = false ; } } // Return the points forming the upper tangent return { a [ inda ] b [ indb ]}; } // Main driver code int main () { vector < vector < int >> a = {{ 2 2 } { 3 1 } { 3 3 } { 5 2 } { 4 0 }}; vector < vector < int >> b = {{ 0 1 } { 1 0 } { 0 -2 } { -1 0 }}; vector < vector < int >> tangent = findUpperTangent ( a b ); for ( auto it : tangent ){ cout < < it [ 0 ] < < ' ' < < it [ 1 ] < < ' n ' ; } return 0 ; }
Java import java.util.* ; class GfG { // Determines the quadrant of a point static int quad ( int [] p ) { if ( p [ 0 ] >= 0 && p [ 1 ] >= 0 ) return 1 ; if ( p [ 0 ] <= 0 && p [ 1 ] >= 0 ) return 2 ; if ( p [ 0 ] <= 0 && p [ 1 ] <= 0 ) return 3 ; return 4 ; } // Checks whether the line is crossing the polygon static int orientation ( int [] a int [] b int [] c ) { int res = ( b [ 1 ] - a [ 1 ] ) * ( c [ 0 ] - b [ 0 ] ) - ( c [ 1 ] - b [ 1 ] ) * ( b [ 0 ] - a [ 0 ] ); if ( res == 0 ) return 0 ; if ( res > 0 ) return 1 ; return - 1 ; } // Compare function for sorting static class PointComparator implements Comparator < int []> { int [] mid ; public PointComparator ( int [] mid ) { this . mid = mid ; } public int compare ( int [] p1 int [] p2 ) { int [] p = { p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ] }; int [] q = { p2 [ 0 ] - mid [ 0 ] p2 [ 1 ] - mid [ 1 ] }; int one = quad ( p ); int two = quad ( q ); if ( one != two ) return one - two ; return p [ 1 ] * q [ 0 ] - q [ 1 ] * p [ 0 ] ; } } // Finds upper tangent of two polygons 'a' and 'b' // represented as 2D arrays and stores the result static int [][] findUpperTangent ( int [][] a int [][] b ) { // n1 -> number of points in polygon a // n2 -> number of points in polygon b int n1 = a . length n2 = b . length ; int [] mid = { 0 0 }; int maxa = Integer . MIN_VALUE ; // Calculate centroid for polygon a and adjust points for scaling for ( int i = 0 ; i < n1 ; i ++ ) { maxa = Math . max ( maxa a [ i ][ 0 ] ); mid [ 0 ] += a [ i ][ 0 ] ; mid [ 1 ] += a [ i ][ 1 ] ; a [ i ][ 0 ] *= n1 ; a [ i ][ 1 ] *= n1 ; } // Sorting the points in counter-clockwise order for polygon a Arrays . sort ( a new PointComparator ( mid )); for ( int i = 0 ; i < n1 ; i ++ ) { a [ i ][ 0 ] /= n1 ; a [ i ][ 1 ] /= n1 ; } mid [ 0 ] = 0 ; mid [ 1 ] = 0 ; int minb = Integer . MAX_VALUE ; // Calculate centroid for polygon b and adjust points for scaling for ( int i = 0 ; i < n2 ; i ++ ) { mid [ 0 ] += b [ i ][ 0 ] ; mid [ 1 ] += b [ i ][ 1 ] ; minb = Math . min ( minb b [ i ][ 0 ] ); b [ i ][ 0 ] *= n2 ; b [ i ][ 1 ] *= n2 ; } // Sorting the points in counter-clockwise order for polygon b Arrays . sort ( b new PointComparator ( mid )); for ( int i = 0 ; i < n2 ; i ++ ) { b [ i ][ 0 ] /= n2 ; b [ i ][ 1 ] /= n2 ; } // If a is to the right of b swap a and b if ( minb < maxa ) { int [][] temp = a ; a = b ; b = temp ; n1 = a . length ; n2 = b . length ; } // ia -> rightmost point of a int ia = 0 ib = 0 ; for ( int i = 1 ; i < n1 ; i ++ ) { if ( a [ i ][ 0 ] > a [ ia ][ 0 ] ) ia = i ; } // ib -> leftmost point of b for ( int i = 1 ; i < n2 ; i ++ ) { if ( b [ i ][ 0 ] < b [ ib ][ 0 ] ) ib = i ; } // Finding the upper tangent int inda = ia indb = ib ; boolean done = false ; while ( ! done ) { done = true ; while ( orientation ( b [ indb ] a [ inda ] a [ ( inda + 1 ) % n1 ] ) > 0 ) inda = ( inda + 1 ) % n1 ; while ( orientation ( a [ inda ] b [ indb ] b [ ( n2 + indb - 1 ) % n2 ] ) < 0 ) { indb = ( n2 + indb - 1 ) % n2 ; done = false ; } } // Returning the upper tangent as a 2D array return new int [][] { { a [ inda ][ 0 ] a [ inda ][ 1 ] } { b [ indb ][ 0 ] b [ indb ][ 1 ] } }; } // Driver code public static void main ( String [] args ) { int [][] a = {{ 2 2 }{ 3 1 }{ 3 3 }{ 5 2 }{ 4 0 }}; int [][] b = {{ 0 1 }{ 1 0 }{ 0 - 2 }{ - 1 0 }}; // Get the upper tangent as a 2D array int [][] upperTangent = findUpperTangent ( a b ); // Store or use the result System . out . println ( upperTangent [ 0 ][ 0 ] + ' ' + upperTangent [ 0 ][ 1 ] ); System . out . println ( upperTangent [ 1 ][ 0 ] + ' ' + upperTangent [ 1 ][ 1 ] ); } }
Python from functools import cmp_to_key def quad ( p ): if p [ 0 ] >= 0 and p [ 1 ] >= 0 : return 1 if p [ 0 ] <= 0 and p [ 1 ] >= 0 : return 2 if p [ 0 ] <= 0 and p [ 1 ] <= 0 : return 3 return 4 def orientation ( a b c ): res = ( b [ 1 ] - a [ 1 ]) * ( c [ 0 ] - b [ 0 ]) - ( c [ 1 ] - b [ 1 ]) * ( b [ 0 ] - a [ 0 ]) if res == 0 : return 0 if res > 0 : return 1 return - 1 def compare ( mid ): def cmp ( p1 q1 ): p = [ p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ]] q = [ q1 [ 0 ] - mid [ 0 ] q1 [ 1 ] - mid [ 1 ]] one = quad ( p ) two = quad ( q ) if one != two : return one - two if p [ 1 ] * q [ 0 ] < q [ 1 ] * p [ 0 ]: return - 1 return 1 return cmp def findUpperTangent ( a b ): n1 n2 = len ( a ) len ( b ) mid_a = [ 0 0 ] maxa = float ( '-inf' ) for i in range ( n1 ): maxa = max ( maxa a [ i ][ 0 ]) mid_a [ 0 ] += a [ i ][ 0 ] mid_a [ 1 ] += a [ i ][ 1 ] a = sorted ( a key = cmp_to_key ( compare ( mid_a ))) mid_b = [ 0 0 ] minb = float ( 'inf' ) for i in range ( n2 ): minb = min ( minb b [ i ][ 0 ]) mid_b [ 0 ] += b [ i ][ 0 ] mid_b [ 1 ] += b [ i ][ 1 ] b = sorted ( b key = cmp_to_key ( compare ( mid_b ))) if minb < maxa : a b = b a n1 n2 = n2 n1 ia = 0 for i in range ( 1 n1 ): if a [ i ][ 0 ] > a [ ia ][ 0 ]: ia = i ib = 0 for i in range ( 1 n2 ): if b [ i ][ 0 ] < b [ ib ][ 0 ]: ib = i inda indb = ia ib done = False while not done : done = True while orientation ( b [ indb ] a [ inda ] a [( inda + 1 ) % n1 ]) > 0 : inda = ( inda + 1 ) % n1 while orientation ( a [ inda ] b [ indb ] b [( n2 + indb - 1 ) % n2 ]) < 0 : indb = ( n2 + indb - 1 ) % n2 done = False # return integer coordinates return [[ int ( a [ inda ][ 0 ]) int ( a [ inda ][ 1 ])] [ int ( b [ indb ][ 0 ]) int ( b [ indb ][ 1 ])]] # Driver Code if __name__ == '__main__' : a = [ [ 2 2 ] [ 3 1 ] [ 3 3 ] [ 5 2 ] [ 4 0 ] ] b = [ [ 0 1 ] [ 1 0 ] [ 0 - 2 ] [ - 1 0 ] ] upperTangent = findUpperTangent ( a b ) for point in upperTangent : print ( f ' { point [ 0 ] } { point [ 1 ] } ' )
C# using System ; public class UpperTangentFinder { static int Quad ( int x int y ) { if ( x >= 0 && y >= 0 ) return 1 ; if ( x <= 0 && y >= 0 ) return 2 ; if ( x <= 0 && y <= 0 ) return 3 ; return 4 ; } static int Orientation ( int [] a int [] b int [] c ) { int res = ( b [ 1 ] - a [ 1 ]) * ( c [ 0 ] - b [ 0 ]) - ( c [ 1 ] - b [ 1 ]) * ( b [ 0 ] - a [ 0 ]); if ( res == 0 ) return 0 ; return res > 0 ? 1 : - 1 ; } static bool Compare ( int [] p1 int [] p2 int [] mid ) { int [] p = { p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ] }; int [] q = { p2 [ 0 ] - mid [ 0 ] p2 [ 1 ] - mid [ 1 ] }; int quadP = Quad ( p [ 0 ] p [ 1 ]); int quadQ = Quad ( q [ 0 ] q [ 1 ]); if ( quadP != quadQ ) return quadP < quadQ ; return ( p [ 1 ] * q [ 0 ]) < ( q [ 1 ] * p [ 0 ]); } static int [] SortPoints ( int [] polygon ) { int n = polygon . GetLength ( 0 ); int [] mid = { 0 0 }; for ( int i = 0 ; i < n ; i ++ ) { mid [ 0 ] += polygon [ i 0 ]; mid [ 1 ] += polygon [ i 1 ]; polygon [ i 0 ] *= n ; polygon [ i 1 ] *= n ; } for ( int i = 0 ; i < n - 1 ; i ++ ) { for ( int j = i + 1 ; j < n ; j ++ ) { int [] p1 = { polygon [ i 0 ] polygon [ i 1 ] }; int [] p2 = { polygon [ j 0 ] polygon [ j 1 ] }; if ( ! Compare ( p1 p2 mid )) { int tempX = polygon [ i 0 ] tempY = polygon [ i 1 ]; polygon [ i 0 ] = polygon [ j 0 ]; polygon [ i 1 ] = polygon [ j 1 ]; polygon [ j 0 ] = tempX ; polygon [ j 1 ] = tempY ; } } } for ( int i = 0 ; i < n ; i ++ ) { polygon [ i 0 ] /= n ; polygon [ i 1 ] /= n ; } return polygon ; } static int [] FindUpperTangent ( int [] a int [] b ) { int n1 = a . GetLength ( 0 ); int n2 = b . GetLength ( 0 ); int maxa = int . MinValue ; for ( int i = 0 ; i < n1 ; i ++ ) maxa = Math . Max ( maxa a [ i 0 ]); int minb = int . MaxValue ; for ( int i = 0 ; i < n2 ; i ++ ) minb = Math . Min ( minb b [ i 0 ]); a = SortPoints ( a ); b = SortPoints ( b ); if ( minb < maxa ) { int [] temp = a ; a = b ; b = temp ; n1 = a . GetLength ( 0 ); n2 = b . GetLength ( 0 ); } int ia = 0 ib = 0 ; for ( int i = 1 ; i < n1 ; i ++ ) if ( a [ i 0 ] > a [ ia 0 ]) ia = i ; for ( int i = 1 ; i < n2 ; i ++ ) if ( b [ i 0 ] < b [ ib 0 ]) ib = i ; int inda = ia indb = ib ; bool done = false ; while ( ! done ) { done = true ; while ( Orientation ( new int [] { b [ indb 0 ] b [ indb 1 ] } new int [] { a [ inda 0 ] a [ inda 1 ] } new int [] { a [( inda + 1 ) % n1 0 ] a [( inda + 1 ) % n1 1 ] }) > 0 ){ inda = ( inda + 1 ) % n1 ; } while ( Orientation ( new int [] { a [ inda 0 ] a [ inda 1 ] } new int [] { b [ indb 0 ] b [ indb 1 ] } new int [] { b [( n2 + indb - 1 ) % n2 0 ] b [( n2 + indb - 1 ) % n2 1 ] }) < 0 ){ indb = ( n2 + indb - 1 ) % n2 ; done = false ; } } int [] result = new int [ 2 2 ]; result [ 0 0 ] = a [ inda 0 ]; result [ 0 1 ] = a [ inda 1 ]; result [ 1 0 ] = b [ indb 0 ]; result [ 1 1 ] = b [ indb 1 ]; return result ; } public static void Main ( string [] args ) { int [] a = new int [] { { 2 2 } { 3 1 } { 3 3 } { 5 2 } { 4 0 } }; int [] b = new int [] { { 0 1 } { 1 0 } { 0 - 2 } { - 1 0 } }; int [] tangent = FindUpperTangent ( a b ); for ( int i = 0 ; i < 2 ; i ++ ) { Console . WriteLine ( tangent [ i 0 ] + ' ' + tangent [ i 1 ]); } } }
JavaScript // Determine the quadrant of a point function quad ( p ) { if ( p [ 0 ] >= 0 && p [ 1 ] >= 0 ) return 1 ; if ( p [ 0 ] <= 0 && p [ 1 ] >= 0 ) return 2 ; if ( p [ 0 ] <= 0 && p [ 1 ] <= 0 ) return 3 ; return 4 ; } // Find orientation of triplet (a b c) function orientation ( a b c ) { let res = ( b [ 1 ] - a [ 1 ]) * ( c [ 0 ] - b [ 0 ]) - ( c [ 1 ] - b [ 1 ]) * ( b [ 0 ] - a [ 0 ]); if ( res === 0 ) return 0 ; return res > 0 ? 1 : - 1 ; } // Compare two points based on mid function compare ( p1 p2 mid ) { let p = [ p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ]]; let q = [ p2 [ 0 ] - mid [ 0 ] p2 [ 1 ] - mid [ 1 ]]; let quadP = quad ( p ); let quadQ = quad ( q ); if ( quadP !== quadQ ) return quadP - quadQ ; return ( p [ 1 ] * q [ 0 ]) - ( q [ 1 ] * p [ 0 ]); } // Sort polygon points counter-clockwise function sortPoints ( polygon ) { let n = polygon . length ; let mid = [ 0 0 ]; for ( let i = 0 ; i < n ; i ++ ) { mid [ 0 ] += polygon [ i ][ 0 ]; mid [ 1 ] += polygon [ i ][ 1 ]; polygon [ i ][ 0 ] *= n ; polygon [ i ][ 1 ] *= n ; } polygon . sort (( p1 p2 ) => compare ( p1 p2 mid )); for ( let i = 0 ; i < n ; i ++ ) { polygon [ i ][ 0 ] = Math . floor ( polygon [ i ][ 0 ] / n ); polygon [ i ][ 1 ] = Math . floor ( polygon [ i ][ 1 ] / n ); } return polygon ; } // Find upper tangent between two convex polygons function findUpperTangent ( a b ) { let n1 = a . length ; let n2 = b . length ; let maxa = - Infinity ; for ( let i = 0 ; i < n1 ; i ++ ) maxa = Math . max ( maxa a [ i ][ 0 ]); let minb = Infinity ; for ( let i = 0 ; i < n2 ; i ++ ) minb = Math . min ( minb b [ i ][ 0 ]); a = sortPoints ( a ); b = sortPoints ( b ); if ( minb < maxa ) { let temp = a ; a = b ; b = temp ; n1 = a . length ; n2 = b . length ; } let ia = 0 ib = 0 ; for ( let i = 1 ; i < n1 ; i ++ ) if ( a [ i ][ 0 ] > a [ ia ][ 0 ]) ia = i ; for ( let i = 1 ; i < n2 ; i ++ ) if ( b [ i ][ 0 ] < b [ ib ][ 0 ]) ib = i ; let inda = ia indb = ib ; let done = false ; while ( ! done ) { done = true ; while ( orientation ( b [ indb ] a [ inda ] a [( inda + 1 ) % n1 ]) > 0 ) inda = ( inda + 1 ) % n1 ; while ( orientation ( a [ inda ] b [ indb ] b [( n2 + indb - 1 ) % n2 ]) < 0 ) { indb = ( n2 + indb - 1 ) % n2 ; done = false ; } } return [ a [ inda ] b [ indb ]]; } // Driver code let a = [[ 2 2 ][ 3 1 ][ 3 3 ][ 5 2 ][ 4 0 ]]; let b = [[ 0 1 ][ 1 0 ][ 0 - 2 ][ - 1 0 ]]; let tangent = findUpperTangent ( a b ); for ( let point of tangent ) { console . log ( point [ 0 ] + ' ' + point [ 1 ]); }
Çıkış
upper tangent (01) (33)
Zaman Karmaşıklığı: O(n1 log (n1) + n2 log(n2))
Yardımcı Alan: Ç(1)