N-ary Ağacı için LCA | Sabit Sorgu O(1)
N-ary ağaçta LCA'yı hesaplamak için farklı Zaman Karmaşıklıklarına sahip çeşitli yöntemler gördük: -
Yöntem 1: Naif Yöntem (kökten düğüme giden yolu hesaplayarak) | Sorgu başına O(n)
Yöntem 2: Sqrt Ayrıştırmayı Kullanma | O(karek H)
Yöntem 3: Seyrek Matris DP yaklaşımını kullanma | O(giriş)
Yukarıdaki yöntemlerin hepsinden daha hızlı sorgulama süresine sahip başka bir yöntemi inceleyelim. Yani amacımız LCA'yı hesaplamak olacaktır. sabit zaman ~ O(1) . Bakalım bunu nasıl başarabiliriz.
Yöntem 4: Aralık Minimum Sorgusunu Kullanma
tartıştık İkili ağaç için LCA ve RMQ . Burada n'li ağaç için LCA problemini RMQ problemine dönüştürmeyi tartışıyoruz.
Pre-requisites:- LCA in Binary Tree using RMQ RMQ using sparse table
Anahtar Konsept: Bu yöntemde LCA problemimizi statik bir dizi üzerinden RMQ(Range Minimum Query) problemine indirgeyeceğiz. Bunu yaptıktan sonra Aralık minimum sorgularını gerekli LCA sorgularıyla ilişkilendireceğiz.
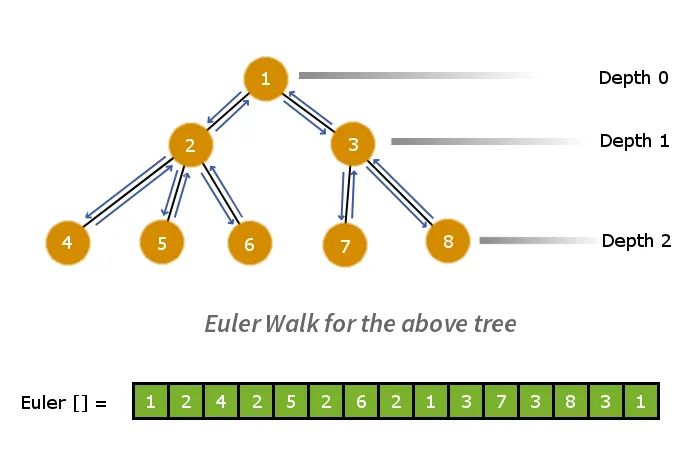
İlk adım, ağacı düz bir doğrusal diziye ayırmak olacaktır. Bunu yapmak için Euler yürüyüşünü uygulayabiliriz. Euler yürüyüşü grafiğin ön sıra geçişini verecektir. Bu yüzden ağaç üzerinde bir Euler Yürüyüşü gerçekleştireceğiz ve düğümleri ziyaret ettiğimizde bir dizide saklayacağız. Bu işlem ağacı azaltır > 
Şimdi genel anlamda düşünelim: Ağaçtaki herhangi iki düğümü düşünün. Hem düğümleri birbirine bağlayan tam olarak bir yol olacak ve yoldaki en küçük derinlik değerine sahip olan düğüm, verilen iki düğümün LCA'sı olacaktır.
Şimdi herhangi iki farklı düğümü ele alalım içinde Ve v Euler yürüyüş dizisinde. Artık u'dan v'ye giden yoldaki tüm öğeler, Euler yürüyüş dizisindeki u ve v düğümlerinin indeksleri arasında yer alacaktır. Bu nedenle, euler dizisindeki u düğümünün indeksi ile v düğümü arasındaki minimum derinliğe sahip düğümü hesaplamamız yeterlidir.
Bunun için, Euler yürüyüş dizisindeki konumlarına karşılık gelen tüm düğümlerin derinliğini içerecek başka bir dizi tutacağız, böylece RMQ algoritmamızı ona uygulayabiliriz.
Aşağıda verilen, derinlik yolu dizisine paralel olan euler yürüme dizisidir.

Örnek: - İki düğümü düşünün düğüm 6 Ve düğüm 7 euler dizisinde. Düğüm 6 ve düğüm 7'nin LCA'sını hesaplamak için, düğüm 6 ve düğüm 7 arasındaki tüm düğümler için en küçük derinlik değerine bakarız.
Öyleyse düğüm 1 en küçüğü var derinlik değeri = 0 ve dolayısıyla düğüm 6 ve düğüm 7 için LCA'dır.

Uygulama: -
We will be maintaining three arrays 1) Euler Path 2) Depth array 3) First Appearance Index
Euler Yolu ve Derinlik dizisi yukarıda açıklananlarla aynıdır
İlk Görünüm Dizini FAI[] : İlk Görünüm Dizini Dizisi, Euler Yolu dizisindeki her düğümün ilk konumu için dizini saklar. FAI[i] = Euler Walk dizisinde i'inci düğümün ilk görünümü.
Yukarıdaki yöntemin uygulaması aşağıda verilmiştir: -
Uygulama:
C++ // C++ program to demonstrate LCA of n-ary tree // in constant time. #include 'bits/stdc++.h' using namespace std ; #define sz 101 vector < int > adj [ sz ]; // stores the tree vector < int > euler ; // tracks the eulerwalk vector < int > depthArr ; // depth for each node corresponding // to eulerwalk int FAI [ sz ]; // stores first appearance index of every node int level [ sz ]; // stores depth for all nodes in the tree int ptr ; // pointer to euler walk int dp [ sz ][ 18 ]; // sparse table int logn [ sz ]; // stores log values int p2 [ 20 ]; // stores power of 2 void buildSparseTable ( int n ) { // initializing sparse table memset ( dp -1 sizeof ( dp )); // filling base case values for ( int i = 1 ; i < n ; i ++ ) dp [ i -1 ][ 0 ] = ( depthArr [ i ] > depthArr [ i -1 ]) ? i -1 : i ; // dp to fill sparse table for ( int l = 1 ; l < 15 ; l ++ ) for ( int i = 0 ; i < n ; i ++ ) if ( dp [ i ][ l -1 ] != -1 and dp [ i + p2 [ l -1 ]][ l -1 ] != -1 ) dp [ i ][ l ] = ( depthArr [ dp [ i ][ l -1 ]] > depthArr [ dp [ i + p2 [ l -1 ]][ l -1 ]]) ? dp [ i + p2 [ l -1 ]][ l -1 ] : dp [ i ][ l -1 ]; else break ; } int query ( int l int r ) { int d = r - l ; int dx = logn [ d ]; if ( l == r ) return l ; if ( depthArr [ dp [ l ][ dx ]] > depthArr [ dp [ r - p2 [ dx ]][ dx ]]) return dp [ r - p2 [ dx ]][ dx ]; else return dp [ l ][ dx ]; } void preprocess () { // memorizing powers of 2 p2 [ 0 ] = 1 ; for ( int i = 1 ; i < 18 ; i ++ ) p2 [ i ] = p2 [ i -1 ] * 2 ; // memorizing all log(n) values int val = 1 ptr = 0 ; for ( int i = 1 ; i < sz ; i ++ ) { logn [ i ] = ptr -1 ; if ( val == i ) { val *= 2 ; logn [ i ] = ptr ; ptr ++ ; } } } /** * Euler Walk ( preorder traversal) * converting tree to linear depthArray * Time Complexity : O(n) * */ void dfs ( int cur int prev int dep ) { // marking FAI for cur node if ( FAI [ cur ] == -1 ) FAI [ cur ] = ptr ; level [ cur ] = dep ; // pushing root to euler walk euler . push_back ( cur ); // incrementing euler walk pointer ptr ++ ; for ( auto x : adj [ cur ]) { if ( x != prev ) { dfs ( x cur dep + 1 ); // pushing cur again in backtrack // of euler walk euler . push_back ( cur ); // increment euler walk pointer ptr ++ ; } } } // Create Level depthArray corresponding // to the Euler walk Array void makeArr () { for ( auto x : euler ) depthArr . push_back ( level [ x ]); } int LCA ( int u int v ) { // trivial case if ( u == v ) return u ; if ( FAI [ u ] > FAI [ v ]) swap ( u v ); // doing RMQ in the required range return euler [ query ( FAI [ u ] FAI [ v ])]; } void addEdge ( int u int v ) { adj [ u ]. push_back ( v ); adj [ v ]. push_back ( u ); } int main ( int argc char const * argv []) { // constructing the described tree int numberOfNodes = 8 ; addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 2 4 ); addEdge ( 2 5 ); addEdge ( 2 6 ); addEdge ( 3 7 ); addEdge ( 3 8 ); // performing required precalculations preprocess (); // doing the Euler walk ptr = 0 ; memset ( FAI -1 sizeof ( FAI )); dfs ( 1 0 0 ); // creating depthArray corresponding to euler[] makeArr (); // building sparse table buildSparseTable ( depthArr . size ()); cout < < 'LCA(67) : ' < < LCA ( 6 7 ) < < ' n ' ; cout < < 'LCA(64) : ' < < LCA ( 6 4 ) < < ' n ' ; return 0 ; }
Java // Java program to demonstrate LCA of n-ary // tree in constant time. import java.util.ArrayList ; import java.util.Arrays ; class GFG { static int sz = 101 ; @SuppressWarnings ( 'unchecked' ) // Stores the tree static ArrayList < Integer >[] adj = new ArrayList [ sz ] ; // Tracks the eulerwalk static ArrayList < Integer > euler = new ArrayList <> (); // Depth for each node corresponding static ArrayList < Integer > depthArr = new ArrayList <> (); // to eulerwalk // Stores first appearance index of every node static int [] FAI = new int [ sz ] ; // Stores depth for all nodes in the tree static int [] level = new int [ sz ] ; // Pointer to euler walk static int ptr ; // Sparse table static int [][] dp = new int [ sz ][ 18 ] ; // Stores log values static int [] logn = new int [ sz ] ; // Stores power of 2 static int [] p2 = new int [ 20 ] ; static void buildSparseTable ( int n ) { // Initializing sparse table for ( int i = 0 ; i < sz ; i ++ ) { for ( int j = 0 ; j < 18 ; j ++ ) { dp [ i ][ j ] = - 1 ; } } // Filling base case values for ( int i = 1 ; i < n ; i ++ ) dp [ i - 1 ][ 0 ] = ( depthArr . get ( i ) > depthArr . get ( i - 1 )) ? i - 1 : i ; // dp to fill sparse table for ( int l = 1 ; l < 15 ; l ++ ) for ( int i = 0 ; i < n ; i ++ ) if ( dp [ i ][ l - 1 ] != - 1 && dp [ i + p2 [ l - 1 ]][ l - 1 ] != - 1 ) dp [ i ][ l ] = ( depthArr . get ( dp [ i ][ l - 1 ] ) > depthArr . get ( dp [ i + p2 [ l - 1 ]][ l - 1 ] )) ? dp [ i + p2 [ l - 1 ]][ l - 1 ] : dp [ i ][ l - 1 ] ; else break ; } static int query ( int l int r ) { int d = r - l ; int dx = logn [ d ] ; if ( l == r ) return l ; if ( depthArr . get ( dp [ l ][ dx ] ) > depthArr . get ( dp [ r - p2 [ dx ]][ dx ] )) return dp [ r - p2 [ dx ]][ dx ] ; else return dp [ l ][ dx ] ; } static void preprocess () { // Memorizing powers of 2 p2 [ 0 ] = 1 ; for ( int i = 1 ; i < 18 ; i ++ ) p2 [ i ] = p2 [ i - 1 ] * 2 ; // Memorizing all log(n) values int val = 1 ptr = 0 ; for ( int i = 1 ; i < sz ; i ++ ) { logn [ i ] = ptr - 1 ; if ( val == i ) { val *= 2 ; logn [ i ] = ptr ; ptr ++ ; } } } // Euler Walk ( preorder traversal) converting // tree to linear depthArray // Time Complexity : O(n) static void dfs ( int cur int prev int dep ) { // Marking FAI for cur node if ( FAI [ cur ] == - 1 ) FAI [ cur ] = ptr ; level [ cur ] = dep ; // Pushing root to euler walk euler . add ( cur ); // Incrementing euler walk pointer ptr ++ ; for ( Integer x : adj [ cur ] ) { if ( x != prev ) { dfs ( x cur dep + 1 ); // Pushing cur again in backtrack // of euler walk euler . add ( cur ); // Increment euler walk pointer ptr ++ ; } } } // Create Level depthArray corresponding // to the Euler walk Array static void makeArr () { for ( Integer x : euler ) depthArr . add ( level [ x ] ); } static int LCA ( int u int v ) { // Trivial case if ( u == v ) return u ; if ( FAI [ u ] > FAI [ v ] ) { int temp = u ; u = v ; v = temp ; } // Doing RMQ in the required range return euler . get ( query ( FAI [ u ] FAI [ v ] )); } static void addEdge ( int u int v ) { adj [ u ] . add ( v ); adj [ v ] . add ( u ); } // Driver code public static void main ( String [] args ) { for ( int i = 0 ; i < sz ; i ++ ) { adj [ i ] = new ArrayList <> (); } // Constructing the described tree int numberOfNodes = 8 ; addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 2 4 ); addEdge ( 2 5 ); addEdge ( 2 6 ); addEdge ( 3 7 ); addEdge ( 3 8 ); // Performing required precalculations preprocess (); // Doing the Euler walk ptr = 0 ; Arrays . fill ( FAI - 1 ); dfs ( 1 0 0 ); // Creating depthArray corresponding to euler[] makeArr (); // Building sparse table buildSparseTable ( depthArr . size ()); System . out . println ( 'LCA(67) : ' + LCA ( 6 7 )); System . out . println ( 'LCA(64) : ' + LCA ( 6 4 )); } } // This code is contributed by sanjeev2552
Python3 # Python program to demonstrate LCA of n-ary tree # in constant time. from typing import List # stores the tree adj = [[] for _ in range ( 101 )] # tracks the eulerwalk euler = [] # depth for each node corresponding to eulerwalk depthArr = [] # stores first appearance index of every node FAI = [ - 1 ] * 101 # stores depth for all nodes in the tree level = [ 0 ] * 101 # pointer to euler walk ptr = 0 # sparse table dp = [[ - 1 ] * 18 for _ in range ( 101 )] # stores log values logn = [ 0 ] * 101 # stores power of 2 p2 = [ 0 ] * 20 def buildSparseTable ( n : int ): # initializing sparse table for i in range ( n ): dp [ i ][ 0 ] = i - 1 if depthArr [ i ] > depthArr [ i - 1 ] else i # dp to fill sparse table for l in range ( 1 15 ): for i in range ( n ): if dp [ i ][ l - 1 ] != - 1 and dp [ i + p2 [ l - 1 ]][ l - 1 ] != - 1 : dp [ i ][ l ] = dp [ i + p2 [ l - 1 ]][ l - 1 ] if depthArr [ dp [ i ][ l - 1 ] ] > depthArr [ dp [ i + p2 [ l - 1 ]][ l - 1 ]] else dp [ i ][ l - 1 ] else : break def query ( l : int r : int ) -> int : d = r - l dx = logn [ d ] if l == r : return l if depthArr [ dp [ l ][ dx ]] > depthArr [ dp [ r - p2 [ dx ]][ dx ]]: return dp [ r - p2 [ dx ]][ dx ] else : return dp [ l ][ dx ] def preprocess (): global ptr # memorizing powers of 2 p2 [ 0 ] = 1 for i in range ( 1 18 ): p2 [ i ] = p2 [ i - 1 ] * 2 # memorizing all log(n) values val = 1 ptr = 0 for i in range ( 1 101 ): logn [ i ] = ptr - 1 if val == i : val *= 2 logn [ i ] = ptr ptr += 1 def dfs ( cur : int prev : int dep : int ): global ptr # marking FAI for cur node if FAI [ cur ] == - 1 : FAI [ cur ] = ptr level [ cur ] = dep # pushing root to euler walk euler . append ( cur ) # incrementing euler walk pointer ptr += 1 for x in adj [ cur ]: if x != prev : dfs ( x cur dep + 1 ) # pushing cur again in backtrack # of euler walk euler . append ( cur ) # increment euler walk pointer ptr += 1 # Create Level depthArray corresponding # to the Euler walk Array def makeArr (): global depthArr for x in euler : depthArr . append ( level [ x ]) def LCA ( u : int v : int ) -> int : # trivial case if u == v : return u if FAI [ u ] > FAI [ v ]: u v = v u # doing RMQ in the required range return euler [ query ( FAI [ u ] FAI [ v ])] def addEdge ( u v ): adj [ u ] . append ( v ) adj [ v ] . append ( u ) # constructing the described tree numberOfNodes = 8 addEdge ( 1 2 ) addEdge ( 1 3 ) addEdge ( 2 4 ) addEdge ( 2 5 ) addEdge ( 2 6 ) addEdge ( 3 7 ) addEdge ( 3 8 ) # performing required precalculations preprocess () # doing the Euler walk ptr = 0 FAI = [ - 1 ] * ( numberOfNodes + 1 ) dfs ( 1 0 0 ) # creating depthArray corresponding to euler[] makeArr () # building sparse table buildSparseTable ( len ( depthArr )) print ( 'LCA(67) : ' LCA ( 6 7 )) print ( 'LCA(64) : ' LCA ( 6 4 ))
C# // C# program to demonstrate LCA of n-ary // tree in constant time. using System ; using System.Collections.Generic ; public class GFG { static int sz = 101 ; // Stores the tree static List < int > [] adj = new List < int > [ sz ]; // Tracks the eulerwalk static List < int > euler = new List < int > (); // Depth for each node corresponding static List < int > depthArr = new List < int > (); // to eulerwalk // Stores first appearance index of every node static int [] FAI = new int [ sz ]; // Stores depth for all nodes in the tree static int [] level = new int [ sz ]; // Pointer to euler walk static int ptr ; // Sparse table static int [] dp = new int [ sz 18 ]; // Stores log values static int [] logn = new int [ sz ]; // Stores power of 2 static int [] p2 = new int [ 20 ]; static void buildSparseTable ( int n ) { // Initializing sparse table for ( int i = 0 ; i < sz ; i ++ ) { for ( int j = 0 ; j < 18 ; j ++ ) { dp [ i j ] = - 1 ; } } // Filling base case values for ( int i = 1 ; i < n ; i ++ ) dp [ i - 1 0 ] = ( depthArr [ i ] > depthArr [ i - 1 ]) ? i - 1 : i ; // dp to fill sparse table for ( int l = 1 ; l < 15 ; l ++ ) for ( int i = 0 ; i < n ; i ++ ) if ( dp [ i l - 1 ] != - 1 && dp [ i + p2 [ l - 1 ] l - 1 ] != - 1 ) dp [ i l ] = ( depthArr [ dp [ i l - 1 ]] > depthArr [ dp [ i + p2 [ l - 1 ] l - 1 ]]) ? dp [ i + p2 [ l - 1 ] l - 1 ] : dp [ i l - 1 ]; else break ; } static int query ( int l int r ) { int d = r - l ; int dx = logn [ d ]; if ( l == r ) return l ; if ( depthArr [ dp [ l dx ]] > depthArr [ dp [ r - p2 [ dx ] dx ]]) return dp [ r - p2 [ dx ] dx ]; else return dp [ l dx ]; } static void preprocess () { // Memorizing powers of 2 p2 [ 0 ] = 1 ; for ( int i = 1 ; i < 18 ; i ++ ) p2 [ i ] = p2 [ i - 1 ] * 2 ; // Memorizing all log(n) values int val = 1 ptr = 0 ; for ( int i = 1 ; i < sz ; i ++ ) { logn [ i ] = ptr - 1 ; if ( val == i ) { val *= 2 ; logn [ i ] = ptr ; ptr ++ ; } } } // Euler Walk ( preorder traversal) converting // tree to linear depthArray // Time Complexity : O(n) static void dfs ( int cur int prev int dep ) { // Marking FAI for cur node if ( FAI [ cur ] == - 1 ) FAI [ cur ] = ptr ; level [ cur ] = dep ; // Pushing root to euler walk euler . Add ( cur ); // Incrementing euler walk pointer ptr ++ ; foreach ( int x in adj [ cur ]) { if ( x != prev ) { dfs ( x cur dep + 1 ); euler . Add ( cur ); ptr ++ ; } } } // Create Level depthArray corresponding // to the Euler walk Array static void makeArr () { foreach ( int x in euler ) depthArr . Add ( level [ x ]); } static int LCA ( int u int v ) { // Trivial case if ( u == v ) return u ; if ( FAI [ u ] > FAI [ v ]) { int temp = u ; u = v ; v = temp ; } // Doing RMQ in the required range return euler [ query ( FAI [ u ] FAI [ v ])]; } static void addEdge ( int u int v ) { adj [ u ]. Add ( v ); adj [ v ]. Add ( u ); } // Driver Code static void Main ( string [] args ) { int sz = 9 ; adj = new List < int > [ sz ]; for ( int i = 0 ; i < sz ; i ++ ) { adj [ i ] = new List < int > (); } // Constructing the described tree int numberOfNodes = 8 ; addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 2 4 ); addEdge ( 2 5 ); addEdge ( 2 6 ); addEdge ( 3 7 ); addEdge ( 3 8 ); // Performing required precalculations preprocess (); // Doing the Euler walk ptr = 0 ; Array . Fill ( FAI - 1 ); dfs ( 1 0 0 ); // Creating depthArray corresponding to euler[] makeArr (); // Building sparse table buildSparseTable ( depthArr . Count ); Console . WriteLine ( 'LCA(67) : ' + LCA ( 6 7 )); Console . WriteLine ( 'LCA(64) : ' + LCA ( 6 4 )); } } // This code is contributed by Prince Kumar
JavaScript let adj = []; for ( let _ = 0 ; _ < 101 ; _ ++ ) { adj . push ([]); } // tracks the eulerwalk let euler = []; // depth for each node corresponding to eulerwalk let depthArr = []; // stores first appearance index of every node let FAI = new Array ( 101 ). fill ( - 1 ); // stores depth for all nodes in the tree let level = new Array ( 101 ). fill ( 0 ); // pointer to euler walk let ptr = 0 ; // sparse table let dp = []; for ( let _ = 0 ; _ < 101 ; _ ++ ) { dp . push ( new Array ( 18 ). fill ( - 1 )); } // stores log values let logn = new Array ( 101 ). fill ( 0 ); // stores power of 2 let p2 = new Array ( 20 ). fill ( 0 ); function buildSparseTable ( n ) { // initializing sparse table for ( let i = 0 ; i < n ; i ++ ) { dp [ i ][ 0 ] = i - 1 >= 0 && depthArr [ i ] > depthArr [ i - 1 ] ? i - 1 : i ; } // dp to fill sparse table for ( let l = 1 ; l < 15 ; l ++ ) { for ( let i = 0 ; i < n ; i ++ ) { if ( dp [ i ][ l - 1 ] !== - 1 && dp [ i + p2 [ l - 1 ]][ l - 1 ] !== - 1 ) { dp [ i ][ l ] = depthArr [ dp [ i ][ l - 1 ]] > depthArr [ dp [ i + p2 [ l - 1 ]][ l - 1 ]] ? dp [ i + p2 [ l - 1 ]][ l - 1 ] : dp [ i ][ l - 1 ]; } else { break ; } } } } function query ( l r ) { let d = r - l ; let dx = logn [ d ]; if ( l === r ) { return l ; } if ( depthArr [ dp [ l ][ dx ]] > depthArr [ dp [ r - p2 [ dx ]][ dx ]]) { return dp [ r - p2 [ dx ]][ dx ]; } else { return dp [ l ][ dx ]; } } function preprocess () { // memorizing powers of 2 p2 [ 0 ] = 1 ; for ( let i = 1 ; i < 18 ; i ++ ) { p2 [ i ] = p2 [ i - 1 ] * 2 ; } // memorizing all log(n) values let val = 1 ; ptr = 0 ; for ( let i = 1 ; i < 101 ; i ++ ) { logn [ i ] = ptr - 1 ; if ( val === i ) { val *= 2 ; logn [ i ] = ptr ; ptr += 1 ; } } } function dfs ( cur prev dep ) { // marking FAI for cur node if ( FAI [ cur ] === - 1 ) { FAI [ cur ] = ptr ; } level [ cur ] = dep ; // pushing root to euler walk euler . push ( cur ); // incrementing euler walk pointer ptr += 1 ; for ( let x of adj [ cur ]) { if ( x !== prev ) { dfs ( x cur dep + 1 ); // pushing cur again in backtrack // of euler walk euler . push ( cur ); // increment euler walk pointer ptr += 1 ; } } } // Create Level depthArray corresponding // to the Euler walk Array function makeArr () { for ( let x of euler ) { depthArr . push ( level [ x ]); } } function LCA ( u v ) { // trivial case if ( u === v ) { return u ; } if ( FAI [ u ] > FAI [ v ]) { [ u v ] = [ v u ]; } // doing RMQ in the required range return euler [ query ( FAI [ u ] FAI [ v ])]; } function addEdge ( u v ) { adj [ u ]. push ( v ); adj [ v ]. push ( u ); } // constructing the described tree let numberOfNodes = 8 ; addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 2 4 ); addEdge ( 2 5 ); addEdge ( 2 6 ); addEdge ( 3 7 ); addEdge ( 3 8 ); // performing required precalculations preprocess (); // doing the Euler walk ptr = 0 ; FAI = new Array ( numberOfNodes + 1 ). fill ( - 1 ); dfs ( 1 0 0 ); // creating depthArray corresponding to euler[] makeArr (); // building sparse table buildSparseTable ( depthArr . length ); console . log ( 'LCA(67) : ' LCA ( 6 7 )); console . log ( 'LCA(64) : ' LCA ( 6 4 ));
Çıkış
LCA(67) : 1 LCA(64) : 2
Not : Sorgu başına sabit zaman karmaşıklığı sağlamak için 2'lerin gerekli tüm gücünü önceden hesaplıyoruz ve ayrıca gerekli tüm günlük değerlerini de önceden hesaplıyoruz. Aksi takdirde her sorgu işlemi için log hesaplaması yapsaydık Zaman karmaşıklığımız sabit olmazdı.
Zaman Karmaşıklığı: LCA'dan RMQ'ya dönüştürme işlemi Euler Walk tarafından yapılır. Açık) zaman.
RMQ'daki seyrek tablonun ön işlenmesi O(nlogn) zaman alır ve her Sorguyu yanıtlamak Sabit zamanlı bir işlemdir. Bu nedenle genel Zaman Karmaşıklığı O(nlogn)'dur - ön işleme ve Ç(1) her sorgu için.
Yardımcı Alan: O(n+s)
Test Oluştur