Bir kümede Ekleme, Silme ve Ortanca sorgularını verimli bir şekilde tasarlayın

Başlangıçta boş bir küme ve bunun üzerinde her biri muhtemelen aşağıdaki türlerden olan bir dizi sorgu verildiğinde:
- 'x' ekleme işlemi update(1 0 10^6 x 1) kullanılarak yapılır. Ağacın kökünün iletildiğini, başlangıç indeksinin 0 olarak ve bitiş indeksinin 10^6 olarak iletildiğini, böylece x'i içeren tüm aralıkların güncellendiğini unutmayın.
- 'x' silme işlemi update(1 0 10^6 x -1) kullanılarak yapılır. Ağacın kökünün iletildiğini, başlangıç indeksinin 0 olarak ve bitiş indeksinin 10^6 olarak iletildiğini, böylece x'i içeren tüm aralıkların güncellendiğini unutmayın.
Örnek:
Input : Insert 1 Insert 4 Insert 7 Median Output : The first three queries should insert 1 4 and 7 into an empty set. The fourth query should return 4 (median of 1 4 7).
Açıklama amacıyla aşağıdakileri varsayıyoruz ancak bu varsayımlar burada tartışılan yöntemin sınırlamaları değildir:
1. Her durumda tüm unsurlar farklıdır, yani hiçbiri birden fazla meydana gelmez.
2. 'Medyan' sorgusu sadece kümede tek sayıda eleman olduğunda yapılır.(Çift sayı olması durumunda segment ağacımızda iki sorgulama yapmamız gerekecek)
3. Kümenin elemanları 1'den +10^6'ya kadar değişir.
Yöntem 1 (Saf)
Saf uygulamada ilk iki sorguyu O(1)'de yapabiliriz, ancak son sorguyu O(max_elem)'de yapabiliriz; burada max_elem tüm zamanların maksimum öğesidir (silinmiş öğeler dahil).
Bir dizi varsayalım saymak[] (boyut 10^6 + 1) alt kümedeki her bir öğenin sayısını korumak için. Aşağıda 3 sorgu için basit ve kendini açıklayan algoritmalar verilmiştir:
X sorgusu ekle:
count[x]++; if (x > max_elem) max_elem = x; n++;
X sorgusunu sil:
if (count[x] > 0) count[x]--; n--;
Medyan sorgusu:
sum = 0; i = 0; while( sum <= n / 2 ) { i++; sum += count[i]; } median = i; return median; Medyan elemanı '7' olan {1 4 7 8 9} kümesini temsil eden dizi sayısı[] gösterimi:

'Medyan' sorgusu, dizideki (n + 1)/2. '1'i, bu durumda 3. '1'i bulmayı amaçlamaktadır; şimdi aynısını bir segment ağacı kullanarak yapıyoruz.
Yöntem 2(Kullanarak Segment Ağacı )
Biz bir segment ağacı aralıkların toplamını saklamak için; burada bir aralık [a b], o anda [a b] aralığındaki kümede bulunan öğelerin sayısını temsil eder. Örneğin yukarıdaki örneği ele alırsak query( 3 7) 2 değerini döndürür query(4 4) 1 değerini döndürür query(5 5) 0 değerini döndürür.
Sorgu ekleme ve silme işlemleri basittir ve her ikisi de update(int x int diff) işlevi kullanılarak uygulanabilir ('x' dizinine 'diff' eklenir)
Algoritma
// adds ‘diff’ at index ‘x’ update(node a b x diff) // If leaf node If a == b and a == x segmentTree[node] += diff // If non-leaf node and x lies in its range If x is in [a b] // Update children recursively update(2*node a (a + b)/2 x diff) update(2*node + 1 (a + b)/2 + 1 b x diff) // Update node segmentTree[node] = segmentTree[2 * node] + segmentTree[2 * node + 1]
Yukarıdaki özyinelemeli işlev çalışır O( günlük( max_elem ) ) (bu durumda max_elem 10^6'dır) ve aşağıdaki çağrılarda hem ekleme hem de silme için kullanılır:
Şimdi, k'inci '1' ile indeksi bulma fonksiyonu, burada 'k' bu durumda her zaman (n + 1) / 2 olacaktır, bu ikili aramaya çok benzer şekilde çalışacaktır, bunu bir bölüm ağacındaki özyinelemeli ikili arama fonksiyonu olarak düşünebilirsiniz.
Kümemizin şu anda { 1 4 7 8 9 } elemanlarına sahip olduğunu ve dolayısıyla aşağıdaki parça ağacıyla temsil edildiğini anlamak için bir örnek alalım.
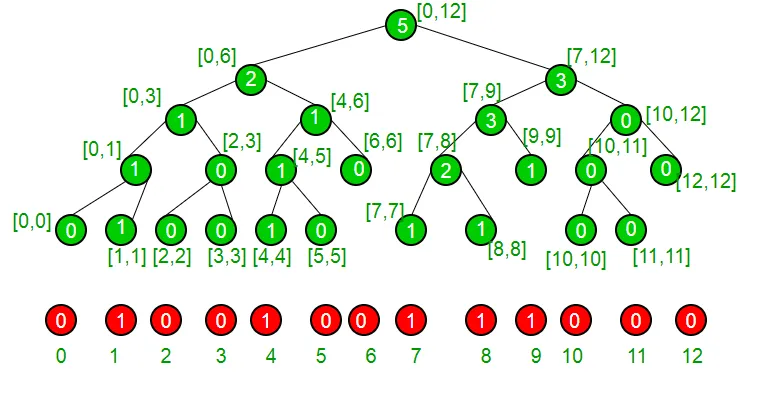
Yaprak olmayan bir düğümdeysek, her iki çocuğunun da olduğundan eminiz, sol çocuğun 'k' olarak daha fazla veya eşit sayıda bire sahip olup olmadığını görürüz, eğer evet ise indeksimizin sol alt ağaçta olduğundan eminiz, aksi takdirde sol alt ağaçta k'den daha az sayıda 1 varsa o zaman indeksimizin sağ alt ağaçta olduğundan eminiz. Dizinimize ulaşmak için bunu yinelemeli olarak yapıyoruz ve oradan geri döndürüyoruz.
Algoritma
1.findKth(node a b k) 2. If a != b 3. If segmentTree[ 2 * node ] >= k 4. return findKth(2*node a (a + b)/2 k) 5. else 6. return findKth(2*node + 1 (a + b)/2 + 1 b k - segmentTree[ 2 * node ]) 7. else 8. return a
Yukarıdaki özyinelemeli işlev çalışır O( log(max_elem)) .
// A C++ program to implement insert delete and // median queries using segment tree #include #define maxn 3000005 #define max_elem 1000000 using namespace std ; // A global array to store segment tree. // Note: Since it is global all elements are 0. int segmentTree [ maxn ]; // Update 'node' and its children in segment tree. // Here 'node' is index in segmentTree[] 'a' and // 'b' are starting and ending indexes of range stored // in current node. // 'diff' is the value to be added to value 'x'. void update ( int node int a int b int x int diff ) { // If current node is a leaf node if ( a == b && a == x ) { // add 'diff' and return segmentTree [ node ] += diff ; return ; } // If current node is non-leaf and 'x' is in its // range if ( x >= a && x <= b ) { // update both sub-trees left and right update ( node * 2 a ( a + b ) / 2 x diff ); update ( node * 2 + 1 ( a + b ) / 2 + 1 b x diff ); // Finally update current node segmentTree [ node ] = segmentTree [ node * 2 ] + segmentTree [ node * 2 + 1 ]; } } // Returns k'th node in segment tree int findKth ( int node int a int b int k ) { // non-leaf node will definitely have both // children; left and right if ( a != b ) { // If kth element lies in the left subtree if ( segmentTree [ node * 2 ] >= k ) return findKth ( node * 2 a ( a + b ) / 2 k ); // If kth one lies in the right subtree return findKth ( node * 2 + 1 ( a + b ) / 2 + 1 b k - segmentTree [ node * 2 ]); } // if at a leaf node return the index it stores // information about return ( segmentTree [ node ]) ? a : -1 ; } // insert x in the set void insert ( int x ) { update ( 1 0 max_elem x 1 ); } // delete x from the set void delete ( int x ) { update ( 1 0 max_elem x -1 ); } // returns median element of the set with odd // cardinality only int median () { int k = ( segmentTree [ 1 ] + 1 ) / 2 ; return findKth ( 1 0 max_elem k ); } // Driver code int main () { insert ( 1 ); insert ( 4 ); insert ( 7 ); cout < < 'Median for the set {147} = ' < < median () < < endl ; insert ( 8 ); insert ( 9 ); cout < < 'Median for the set {14789} = ' < < median () < < endl ; delete ( 1 ); delete ( 8 ); cout < < 'Median for the set {479} = ' < < median () < < endl ; return 0 ; }
Java // A Java program to implement insert delete and // median queries using segment tree import java.io.* ; class GFG { public static int maxn = 3000005 ; public static int max_elem = 1000000 ; // A global array to store segment tree. // Note: Since it is global all elements are 0. public static int [] segmentTree = new int [ maxn ] ; // Update 'node' and its children in segment tree. // Here 'node' is index in segmentTree[] 'a' and // 'b' are starting and ending indexes of range stored // in current node. // 'diff' is the value to be added to value 'x'. public static void update ( int node int a int b int x int diff ) { // If current node is a leaf node if ( a == b && a == x ) { // Add 'diff' and return segmentTree [ node ] += diff ; return ; } // If current node is non-leaf and 'x' // is in its range if ( x >= a && x <= b ) { // Update both sub-trees left and right update ( node * 2 a ( a + b ) / 2 x diff ); update ( node * 2 + 1 ( a + b ) / 2 + 1 b x diff ); // Finally update current node segmentTree [ node ] = segmentTree [ node * 2 ] + segmentTree [ node * 2 + 1 ] ; } } // Returns k'th node in segment tree public static int findKth ( int node int a int b int k ) { // Non-leaf node will definitely have both // children; left and right if ( a != b ) { // If kth element lies in the left subtree if ( segmentTree [ node * 2 ] >= k ) { return findKth ( node * 2 a ( a + b ) / 2 k ); } // If kth one lies in the right subtree return findKth ( node * 2 + 1 ( a + b ) / 2 + 1 b k - segmentTree [ node * 2 ] ); } // If at a leaf node return the index it stores // information about return ( segmentTree [ node ] != 0 ) ? a : - 1 ; } // Insert x in the set public static void insert ( int x ) { update ( 1 0 max_elem x 1 ); } // Delete x from the set public static void delete ( int x ) { update ( 1 0 max_elem x - 1 ); } // Returns median element of the set // with odd cardinality only public static int median () { int k = ( segmentTree [ 1 ] + 1 ) / 2 ; return findKth ( 1 0 max_elem k ); } // Driver code public static void main ( String [] args ) { insert ( 1 ); insert ( 4 ); insert ( 7 ); System . out . println ( 'Median for the set {147} = ' + median ()); insert ( 8 ); insert ( 9 ); System . out . println ( 'Median for the set {14789} = ' + median ()); delete ( 1 ); delete ( 8 ); System . out . println ( 'Median for the set {479} = ' + median ()); } } // This code is contributed by avanitrachhadiya2155
Python3 # A Python3 program to implement insert delete and # median queries using segment tree maxn = 3000005 max_elem = 1000000 # A global array to store segment tree. # Note: Since it is global all elements are 0. segmentTree = [ 0 for i in range ( maxn )] # Update 'node' and its children in segment tree. # Here 'node' is index in segmentTree[] 'a' and # 'b' are starting and ending indexes of range stored # in current node. # 'diff' is the value to be added to value 'x'. def update ( node a b x diff ): global segmentTree # If current node is a leaf node if ( a == b and a == x ): # add 'diff' and return segmentTree [ node ] += diff return # If current node is non-leaf and 'x' is in its # range if ( x >= a and x <= b ): # update both sub-trees left and right update ( node * 2 a ( a + b ) // 2 x diff ) update ( node * 2 + 1 ( a + b ) // 2 + 1 b x diff ) # Finally update current node segmentTree [ node ] = segmentTree [ node * 2 ] + segmentTree [ node * 2 + 1 ] # Returns k'th node in segment tree def findKth ( node a b k ): global segmentTree # non-leaf node will definitely have both # children left and right if ( a != b ): # If kth element lies in the left subtree if ( segmentTree [ node * 2 ] >= k ): return findKth ( node * 2 a ( a + b ) // 2 k ) # If kth one lies in the right subtree return findKth ( node * 2 + 1 ( a + b ) // 2 + 1 b k - segmentTree [ node * 2 ]) # if at a leaf node return the index it stores # information about return a if ( segmentTree [ node ]) else - 1 # insert x in the set def insert ( x ): update ( 1 0 max_elem x 1 ) # delete x from the set def delete ( x ): update ( 1 0 max_elem x - 1 ) # returns median element of the set with odd # cardinality only def median (): k = ( segmentTree [ 1 ] + 1 ) // 2 return findKth ( 1 0 max_elem k ) # Driver code if __name__ == '__main__' : insert ( 1 ) insert ( 4 ) insert ( 7 ) print ( 'Median for the set {147} =' median ()) insert ( 8 ) insert ( 9 ) print ( 'Median for the set {14789} =' median ()) delete ( 1 ) delete ( 8 ) print ( 'Median for the set {479} =' median ()) # This code is contributed by mohit kumar 29
C# // A C# program to implement insert delete // and median queries using segment tree using System ; class GFG { public static int maxn = 3000005 ; public static int max_elem = 1000000 ; // A global array to store segment tree. // Note: Since it is global all elements are 0. public static int [] segmentTree = new int [ maxn ]; // Update 'node' and its children in segment tree. // Here 'node' is index in segmentTree[] 'a' and // 'b' are starting and ending indexes of range stored // in current node. // 'diff' is the value to be added to value 'x'. public static void update ( int node int a int b int x int diff ) { // If current node is a leaf node if ( a == b && a == x ) { // Add 'diff' and return segmentTree [ node ] += diff ; return ; } // If current node is non-leaf and 'x' // is in its range if ( x >= a && x <= b ) { // Update both sub-trees left and right update ( node * 2 a ( a + b ) / 2 x diff ); update ( node * 2 + 1 ( a + b ) / 2 + 1 b x diff ); // Finally update current node segmentTree [ node ] = segmentTree [ node * 2 ] + segmentTree [ node * 2 + 1 ]; } } // Returns k'th node in segment tree public static int findKth ( int node int a int b int k ) { // Non-leaf node will definitely have both // children; left and right if ( a != b ) { // If kth element lies in the left subtree if ( segmentTree [ node * 2 ] >= k ) { return findKth ( node * 2 a ( a + b ) / 2 k ); } // If kth one lies in the right subtree return findKth ( node * 2 + 1 ( a + b ) / 2 + 1 b k - segmentTree [ node * 2 ]); } // If at a leaf node return the index it // stores information about if ( segmentTree [ node ] != 0 ) { return a ; } else { return - 1 ; } } // Insert x in the set public static void insert ( int x ) { update ( 1 0 max_elem x 1 ); } // Delete x from the set public static void delete ( int x ) { update ( 1 0 max_elem x - 1 ); } // Returns median element of the set // with odd cardinality only public static int median () { int k = ( segmentTree [ 1 ] + 1 ) / 2 ; return findKth ( 1 0 max_elem k ); } // Driver code static public void Main () { insert ( 1 ); insert ( 4 ); insert ( 7 ); Console . WriteLine ( 'Median for the set {147} = ' + median ()); insert ( 8 ); insert ( 9 ); Console . WriteLine ( 'Median for the set {14789} = ' + median ()); delete ( 1 ); delete ( 8 ); Console . WriteLine ( 'Median for the set {479} = ' + median ()); } } // This code is contributed by rag2127
JavaScript < script > // A Javascript program to implement insert delete and // median queries using segment tree let maxn = 3000005 ; let max_elem = 1000000 ; // A global array to store segment tree. // Note: Since it is global all elements are 0. let segmentTree = new Array ( maxn ); for ( let i = 0 ; i < maxn ; i ++ ) { segmentTree [ i ] = 0 ; } // Update 'node' and its children in segment tree. // Here 'node' is index in segmentTree[] 'a' and // 'b' are starting and ending indexes of range stored // in current node. // 'diff' is the value to be added to value 'x'. function update ( node a b x diff ) { // If current node is a leaf node if ( a == b && a == x ) { // Add 'diff' and return segmentTree [ node ] += diff ; return ; } // If current node is non-leaf and 'x' // is in its range if ( x >= a && x <= b ) { // Update both sub-trees left and right update ( node * 2 a Math . floor (( a + b ) / 2 ) x diff ); update ( node * 2 + 1 Math . floor (( a + b ) / 2 ) + 1 b x diff ); // Finally update current node segmentTree [ node ] = segmentTree [ node * 2 ] + segmentTree [ node * 2 + 1 ]; } } // Returns k'th node in segment tree function findKth ( node a b k ) { // Non-leaf node will definitely have both // children; left and right if ( a != b ) { // If kth element lies in the left subtree if ( segmentTree [ node * 2 ] >= k ) { return findKth ( node * 2 a Math . floor (( a + b ) / 2 ) k ); } // If kth one lies in the right subtree return findKth ( node * 2 + 1 Math . floor (( a + b ) / 2 ) + 1 b k - segmentTree [ node * 2 ]); } // If at a leaf node return the index it stores // information about return ( segmentTree [ node ] != 0 ) ? a : - 1 ; } // Insert x in the set function insert ( x ) { update ( 1 0 max_elem x 1 ); } // Delete x from the set function delet ( x ) { update ( 1 0 max_elem x - 1 ); } // Returns median element of the set // with odd cardinality only function median () { let k = ( segmentTree [ 1 ] + 1 ) / 2 ; return findKth ( 1 0 max_elem k ); } // Driver code insert ( 1 ); insert ( 4 ); insert ( 7 ); document . write ( 'Median for the set {147} = ' + median () + '
' ); insert ( 8 ); insert ( 9 ); document . write ( 'Median for the set {14789} = ' + median () + '
' ); delet ( 1 ); delet ( 8 ); document . write ( 'Median for the set {479} = ' + median () + '
' ); // This code is contributed by unknown2108 < /script>
Çıkış:
Median for the set {147} = 4 Median for the set {14789} = 7 Median for the set {479} = 7
Çözüm:
Her üç sorgu da çalıştırılıyor O( log(max_elem)) bu durumda max_elem = 10^6 yani log(max_elem) yaklaşık olarak 20'ye eşittir.
Segment ağacının kullandığı Ç(max_elem) uzay.
Silme sorgusu olmasaydı sorun ünlü bir algoritmayla da çözülmüş olabilirdi Burada .