Tangentes entre deux polygones convexes
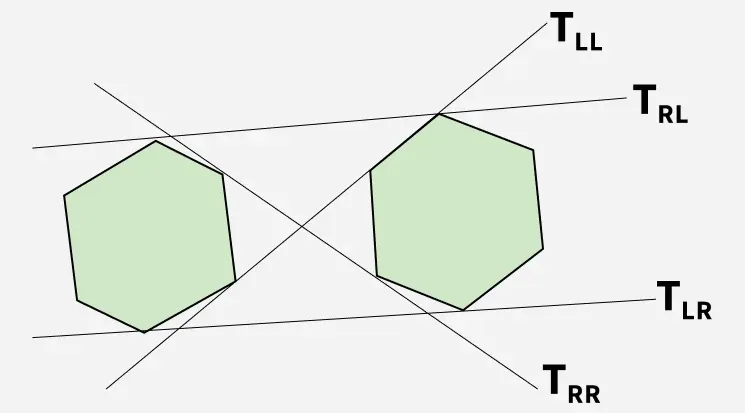
Étant donné deux polygones convexes, nous visons à identifier les tangentes inférieure et supérieure qui les relient.
Comme le montre la figure ci-dessous T R.L. et T LR représentent respectivement les tangentes supérieure et inférieure.

Exemples :
Saisir: Premier polygone : [[2 2] [3 3] [5 2] [4 0] [3 1]]
Deuxième polygone : [[-1 0] [0 1] [1 0] [0 -2]].
Sortir: Tangente supérieure - ligne joignant (01) et (33)
Tangente inférieure - ligne joignant (0-2) et (40)
Explication: L'image montre clairement la structure et les tangentes reliant les deux polygones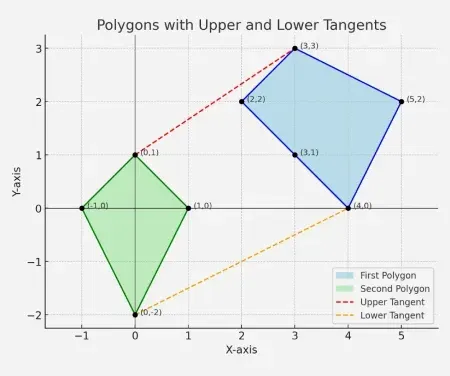
Approche:
Pour trouver la tangente supérieure, nous commençons par sélectionner deux points : le point le plus à droite du polygone un et le point le plus à gauche du polygone b . La ligne reliant ces deux points est notée Ligne 1 . Puisque cette ligne passe par un polygone b (c'est-à-dire qu'il n'est pas complètement au-dessus), nous passons au point suivant dans le sens inverse des aiguilles d'une montre sur b formation Doubler 2 . Cette ligne est maintenant au-dessus du polygone b ce qui est bien. Cependant il traverse le polygone un nous passons donc au point suivant un dans le sens des aiguilles d'une montre en créant Ligne 3 . Ligne 3 traverse toujours le polygone un provoquant un autre mouvement vers Ligne 4 . Ligne 4 mais traverse le polygone b donc nous procédons à Ligne 5 . Enfin Ligne 5 ne traverse aucun des polygones, ce qui en fait la tangente supérieure correcte pour les polygones donnés.
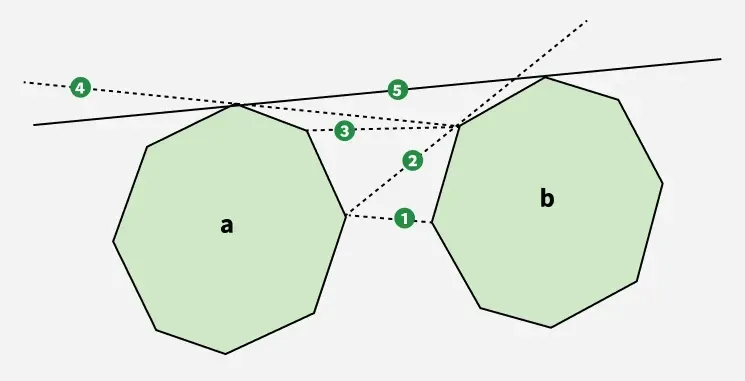
Pour trouver la tangente inférieure, nous devons nous déplacer inversement à travers les polygones, c'est-à-dire que si la ligne traverse le polygone b, nous nous déplaçons ensuite dans le sens des aiguilles d'une montre et dans le sens inverse des aiguilles d'une montre si la ligne traverse le polygone a.
Algorithme pour la tangente supérieure :
L ← ligne joignant le point le plus à droite de a et le point le plus à gauche de b. while (L traverse l'un des polygones) { while (L traverse b) L ← L' : le point sur b monte. tandis que (L croise a) L ← L' : le point sur a monte. }
Algorithme pour la tangente inférieure :
L ← ligne joignant le point le plus à droite de a et le point le plus à gauche de b. while (L traverse l'un des polygones) { while (L traverse b) L ← L' : le point sur b descend. tandis que (L croise a) L ← L' : le point sur a descend. }
Notez que le code ci-dessus calcule uniquement la tangente supérieure. Une approche similaire peut également être utilisée pour trouver la tangente inférieure.
CPP #include using namespace std ; // Determines the quadrant of a point relative to origin int quad ( vector < int > p ) { if ( p [ 0 ] >= 0 && p [ 1 ] >= 0 ) return 1 ; if ( p [ 0 ] <= 0 && p [ 1 ] >= 0 ) return 2 ; if ( p [ 0 ] <= 0 && p [ 1 ] <= 0 ) return 3 ; return 4 ; } // Returns the orientation of ordered triplet (a b c) // 0 -> Collinear 1 -> Clockwise -1 -> Counterclockwise int orientation ( vector < int > a vector < int > b vector < int > c ) { int res = ( b [ 1 ] - a [ 1 ]) * ( c [ 0 ] - b [ 0 ]) - ( c [ 1 ] - b [ 1 ]) * ( b [ 0 ] - a [ 0 ]); if ( res == 0 ) return 0 ; if ( res > 0 ) return 1 ; return -1 ; } // Compare function to sort points counter-clockwise around center bool compare ( vector < int > p1 vector < int > q1 vector < int > mid ) { vector < int > p = { p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ]}; vector < int > q = { q1 [ 0 ] - mid [ 0 ] q1 [ 1 ] - mid [ 1 ]}; int one = quad ( p ); int two = quad ( q ); if ( one != two ) return ( one < two ); return ( p [ 1 ] * q [ 0 ] < q [ 1 ] * p [ 0 ]); } // Sorts the polygon points counter-clockwise vector < vector < int >> sortPoints ( vector < vector < int >> polygon ) { vector < int > mid = { 0 0 }; int n = polygon . size (); // Calculate center (centroid) of the polygon for ( int i = 0 ; i < n ; i ++ ) { mid [ 0 ] += polygon [ i ][ 0 ]; mid [ 1 ] += polygon [ i ][ 1 ]; polygon [ i ][ 0 ] *= n ; polygon [ i ][ 1 ] *= n ; } // Sort points based on their angle from the center sort ( polygon . begin () polygon . end () [ mid ]( vector < int > p1 vector < int > p2 ) { return compare ( p1 p2 mid ); }); // Divide back to original coordinates for ( int i = 0 ; i < n ; i ++ ) { polygon [ i ][ 0 ] /= n ; polygon [ i ][ 1 ] /= n ; } return polygon ; } // Finds the upper tangent between two convex polygons a and b // Returns two points forming the upper tangent vector < vector < int >> findUpperTangent ( vector < vector < int >> a vector < vector < int >> b ) { int n1 = a . size () n2 = b . size (); // Find the rightmost point of polygon a and leftmost point of polygon b int maxa = INT_MIN ; for ( auto & p : a ) maxa = max ( maxa p [ 0 ]); int minb = INT_MAX ; for ( auto & p : b ) minb = min ( minb p [ 0 ]); // Sort both polygons counter-clockwise a = sortPoints ( a ); b = sortPoints ( b ); // Ensure polygon a is to the left of polygon b if ( minb < maxa ) swap ( a b ); n1 = a . size (); n2 = b . size (); // Find the rightmost point in a int ia = 0 ib = 0 ; for ( int i = 1 ; i < n1 ; i ++ ) if ( a [ i ][ 0 ] > a [ ia ][ 0 ]) ia = i ; // Find the leftmost point in b for ( int i = 1 ; i < n2 ; i ++ ) if ( b [ i ][ 0 ] < b [ ib ][ 0 ]) ib = i ; // Initialize starting points int inda = ia indb = ib ; bool done = false ; // Find upper tangent using orientation checks while ( ! done ) { done = true ; // Move to next point in a if necessary while ( orientation ( b [ indb ] a [ inda ] a [( inda + 1 ) % n1 ]) > 0 ) inda = ( inda + 1 ) % n1 ; // Move to previous point in b if necessary while ( orientation ( a [ inda ] b [ indb ] b [( n2 + indb - 1 ) % n2 ]) < 0 ) { indb = ( n2 + indb - 1 ) % n2 ; done = false ; } } // Return the points forming the upper tangent return { a [ inda ] b [ indb ]}; } // Main driver code int main () { vector < vector < int >> a = {{ 2 2 } { 3 1 } { 3 3 } { 5 2 } { 4 0 }}; vector < vector < int >> b = {{ 0 1 } { 1 0 } { 0 -2 } { -1 0 }}; vector < vector < int >> tangent = findUpperTangent ( a b ); for ( auto it : tangent ){ cout < < it [ 0 ] < < ' ' < < it [ 1 ] < < ' n ' ; } return 0 ; }
Java import java.util.* ; class GfG { // Determines the quadrant of a point static int quad ( int [] p ) { if ( p [ 0 ] >= 0 && p [ 1 ] >= 0 ) return 1 ; if ( p [ 0 ] <= 0 && p [ 1 ] >= 0 ) return 2 ; if ( p [ 0 ] <= 0 && p [ 1 ] <= 0 ) return 3 ; return 4 ; } // Checks whether the line is crossing the polygon static int orientation ( int [] a int [] b int [] c ) { int res = ( b [ 1 ] - a [ 1 ] ) * ( c [ 0 ] - b [ 0 ] ) - ( c [ 1 ] - b [ 1 ] ) * ( b [ 0 ] - a [ 0 ] ); if ( res == 0 ) return 0 ; if ( res > 0 ) return 1 ; return - 1 ; } // Compare function for sorting static class PointComparator implements Comparator < int []> { int [] mid ; public PointComparator ( int [] mid ) { this . mid = mid ; } public int compare ( int [] p1 int [] p2 ) { int [] p = { p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ] }; int [] q = { p2 [ 0 ] - mid [ 0 ] p2 [ 1 ] - mid [ 1 ] }; int one = quad ( p ); int two = quad ( q ); if ( one != two ) return one - two ; return p [ 1 ] * q [ 0 ] - q [ 1 ] * p [ 0 ] ; } } // Finds upper tangent of two polygons 'a' and 'b' // represented as 2D arrays and stores the result static int [][] findUpperTangent ( int [][] a int [][] b ) { // n1 -> number of points in polygon a // n2 -> number of points in polygon b int n1 = a . length n2 = b . length ; int [] mid = { 0 0 }; int maxa = Integer . MIN_VALUE ; // Calculate centroid for polygon a and adjust points for scaling for ( int i = 0 ; i < n1 ; i ++ ) { maxa = Math . max ( maxa a [ i ][ 0 ] ); mid [ 0 ] += a [ i ][ 0 ] ; mid [ 1 ] += a [ i ][ 1 ] ; a [ i ][ 0 ] *= n1 ; a [ i ][ 1 ] *= n1 ; } // Sorting the points in counter-clockwise order for polygon a Arrays . sort ( a new PointComparator ( mid )); for ( int i = 0 ; i < n1 ; i ++ ) { a [ i ][ 0 ] /= n1 ; a [ i ][ 1 ] /= n1 ; } mid [ 0 ] = 0 ; mid [ 1 ] = 0 ; int minb = Integer . MAX_VALUE ; // Calculate centroid for polygon b and adjust points for scaling for ( int i = 0 ; i < n2 ; i ++ ) { mid [ 0 ] += b [ i ][ 0 ] ; mid [ 1 ] += b [ i ][ 1 ] ; minb = Math . min ( minb b [ i ][ 0 ] ); b [ i ][ 0 ] *= n2 ; b [ i ][ 1 ] *= n2 ; } // Sorting the points in counter-clockwise order for polygon b Arrays . sort ( b new PointComparator ( mid )); for ( int i = 0 ; i < n2 ; i ++ ) { b [ i ][ 0 ] /= n2 ; b [ i ][ 1 ] /= n2 ; } // If a is to the right of b swap a and b if ( minb < maxa ) { int [][] temp = a ; a = b ; b = temp ; n1 = a . length ; n2 = b . length ; } // ia -> rightmost point of a int ia = 0 ib = 0 ; for ( int i = 1 ; i < n1 ; i ++ ) { if ( a [ i ][ 0 ] > a [ ia ][ 0 ] ) ia = i ; } // ib -> leftmost point of b for ( int i = 1 ; i < n2 ; i ++ ) { if ( b [ i ][ 0 ] < b [ ib ][ 0 ] ) ib = i ; } // Finding the upper tangent int inda = ia indb = ib ; boolean done = false ; while ( ! done ) { done = true ; while ( orientation ( b [ indb ] a [ inda ] a [ ( inda + 1 ) % n1 ] ) > 0 ) inda = ( inda + 1 ) % n1 ; while ( orientation ( a [ inda ] b [ indb ] b [ ( n2 + indb - 1 ) % n2 ] ) < 0 ) { indb = ( n2 + indb - 1 ) % n2 ; done = false ; } } // Returning the upper tangent as a 2D array return new int [][] { { a [ inda ][ 0 ] a [ inda ][ 1 ] } { b [ indb ][ 0 ] b [ indb ][ 1 ] } }; } // Driver code public static void main ( String [] args ) { int [][] a = {{ 2 2 }{ 3 1 }{ 3 3 }{ 5 2 }{ 4 0 }}; int [][] b = {{ 0 1 }{ 1 0 }{ 0 - 2 }{ - 1 0 }}; // Get the upper tangent as a 2D array int [][] upperTangent = findUpperTangent ( a b ); // Store or use the result System . out . println ( upperTangent [ 0 ][ 0 ] + ' ' + upperTangent [ 0 ][ 1 ] ); System . out . println ( upperTangent [ 1 ][ 0 ] + ' ' + upperTangent [ 1 ][ 1 ] ); } }
Python from functools import cmp_to_key def quad ( p ): if p [ 0 ] >= 0 and p [ 1 ] >= 0 : return 1 if p [ 0 ] <= 0 and p [ 1 ] >= 0 : return 2 if p [ 0 ] <= 0 and p [ 1 ] <= 0 : return 3 return 4 def orientation ( a b c ): res = ( b [ 1 ] - a [ 1 ]) * ( c [ 0 ] - b [ 0 ]) - ( c [ 1 ] - b [ 1 ]) * ( b [ 0 ] - a [ 0 ]) if res == 0 : return 0 if res > 0 : return 1 return - 1 def compare ( mid ): def cmp ( p1 q1 ): p = [ p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ]] q = [ q1 [ 0 ] - mid [ 0 ] q1 [ 1 ] - mid [ 1 ]] one = quad ( p ) two = quad ( q ) if one != two : return one - two if p [ 1 ] * q [ 0 ] < q [ 1 ] * p [ 0 ]: return - 1 return 1 return cmp def findUpperTangent ( a b ): n1 n2 = len ( a ) len ( b ) mid_a = [ 0 0 ] maxa = float ( '-inf' ) for i in range ( n1 ): maxa = max ( maxa a [ i ][ 0 ]) mid_a [ 0 ] += a [ i ][ 0 ] mid_a [ 1 ] += a [ i ][ 1 ] a = sorted ( a key = cmp_to_key ( compare ( mid_a ))) mid_b = [ 0 0 ] minb = float ( 'inf' ) for i in range ( n2 ): minb = min ( minb b [ i ][ 0 ]) mid_b [ 0 ] += b [ i ][ 0 ] mid_b [ 1 ] += b [ i ][ 1 ] b = sorted ( b key = cmp_to_key ( compare ( mid_b ))) if minb < maxa : a b = b a n1 n2 = n2 n1 ia = 0 for i in range ( 1 n1 ): if a [ i ][ 0 ] > a [ ia ][ 0 ]: ia = i ib = 0 for i in range ( 1 n2 ): if b [ i ][ 0 ] < b [ ib ][ 0 ]: ib = i inda indb = ia ib done = False while not done : done = True while orientation ( b [ indb ] a [ inda ] a [( inda + 1 ) % n1 ]) > 0 : inda = ( inda + 1 ) % n1 while orientation ( a [ inda ] b [ indb ] b [( n2 + indb - 1 ) % n2 ]) < 0 : indb = ( n2 + indb - 1 ) % n2 done = False # return integer coordinates return [[ int ( a [ inda ][ 0 ]) int ( a [ inda ][ 1 ])] [ int ( b [ indb ][ 0 ]) int ( b [ indb ][ 1 ])]] # Driver Code if __name__ == '__main__' : a = [ [ 2 2 ] [ 3 1 ] [ 3 3 ] [ 5 2 ] [ 4 0 ] ] b = [ [ 0 1 ] [ 1 0 ] [ 0 - 2 ] [ - 1 0 ] ] upperTangent = findUpperTangent ( a b ) for point in upperTangent : print ( f ' { point [ 0 ] } { point [ 1 ] } ' )
C# using System ; public class UpperTangentFinder { static int Quad ( int x int y ) { if ( x >= 0 && y >= 0 ) return 1 ; if ( x <= 0 && y >= 0 ) return 2 ; if ( x <= 0 && y <= 0 ) return 3 ; return 4 ; } static int Orientation ( int [] a int [] b int [] c ) { int res = ( b [ 1 ] - a [ 1 ]) * ( c [ 0 ] - b [ 0 ]) - ( c [ 1 ] - b [ 1 ]) * ( b [ 0 ] - a [ 0 ]); if ( res == 0 ) return 0 ; return res > 0 ? 1 : - 1 ; } static bool Compare ( int [] p1 int [] p2 int [] mid ) { int [] p = { p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ] }; int [] q = { p2 [ 0 ] - mid [ 0 ] p2 [ 1 ] - mid [ 1 ] }; int quadP = Quad ( p [ 0 ] p [ 1 ]); int quadQ = Quad ( q [ 0 ] q [ 1 ]); if ( quadP != quadQ ) return quadP < quadQ ; return ( p [ 1 ] * q [ 0 ]) < ( q [ 1 ] * p [ 0 ]); } static int [] SortPoints ( int [] polygon ) { int n = polygon . GetLength ( 0 ); int [] mid = { 0 0 }; for ( int i = 0 ; i < n ; i ++ ) { mid [ 0 ] += polygon [ i 0 ]; mid [ 1 ] += polygon [ i 1 ]; polygon [ i 0 ] *= n ; polygon [ i 1 ] *= n ; } for ( int i = 0 ; i < n - 1 ; i ++ ) { for ( int j = i + 1 ; j < n ; j ++ ) { int [] p1 = { polygon [ i 0 ] polygon [ i 1 ] }; int [] p2 = { polygon [ j 0 ] polygon [ j 1 ] }; if ( ! Compare ( p1 p2 mid )) { int tempX = polygon [ i 0 ] tempY = polygon [ i 1 ]; polygon [ i 0 ] = polygon [ j 0 ]; polygon [ i 1 ] = polygon [ j 1 ]; polygon [ j 0 ] = tempX ; polygon [ j 1 ] = tempY ; } } } for ( int i = 0 ; i < n ; i ++ ) { polygon [ i 0 ] /= n ; polygon [ i 1 ] /= n ; } return polygon ; } static int [] FindUpperTangent ( int [] a int [] b ) { int n1 = a . GetLength ( 0 ); int n2 = b . GetLength ( 0 ); int maxa = int . MinValue ; for ( int i = 0 ; i < n1 ; i ++ ) maxa = Math . Max ( maxa a [ i 0 ]); int minb = int . MaxValue ; for ( int i = 0 ; i < n2 ; i ++ ) minb = Math . Min ( minb b [ i 0 ]); a = SortPoints ( a ); b = SortPoints ( b ); if ( minb < maxa ) { int [] temp = a ; a = b ; b = temp ; n1 = a . GetLength ( 0 ); n2 = b . GetLength ( 0 ); } int ia = 0 ib = 0 ; for ( int i = 1 ; i < n1 ; i ++ ) if ( a [ i 0 ] > a [ ia 0 ]) ia = i ; for ( int i = 1 ; i < n2 ; i ++ ) if ( b [ i 0 ] < b [ ib 0 ]) ib = i ; int inda = ia indb = ib ; bool done = false ; while ( ! done ) { done = true ; while ( Orientation ( new int [] { b [ indb 0 ] b [ indb 1 ] } new int [] { a [ inda 0 ] a [ inda 1 ] } new int [] { a [( inda + 1 ) % n1 0 ] a [( inda + 1 ) % n1 1 ] }) > 0 ){ inda = ( inda + 1 ) % n1 ; } while ( Orientation ( new int [] { a [ inda 0 ] a [ inda 1 ] } new int [] { b [ indb 0 ] b [ indb 1 ] } new int [] { b [( n2 + indb - 1 ) % n2 0 ] b [( n2 + indb - 1 ) % n2 1 ] }) < 0 ){ indb = ( n2 + indb - 1 ) % n2 ; done = false ; } } int [] result = new int [ 2 2 ]; result [ 0 0 ] = a [ inda 0 ]; result [ 0 1 ] = a [ inda 1 ]; result [ 1 0 ] = b [ indb 0 ]; result [ 1 1 ] = b [ indb 1 ]; return result ; } public static void Main ( string [] args ) { int [] a = new int [] { { 2 2 } { 3 1 } { 3 3 } { 5 2 } { 4 0 } }; int [] b = new int [] { { 0 1 } { 1 0 } { 0 - 2 } { - 1 0 } }; int [] tangent = FindUpperTangent ( a b ); for ( int i = 0 ; i < 2 ; i ++ ) { Console . WriteLine ( tangent [ i 0 ] + ' ' + tangent [ i 1 ]); } } }
JavaScript // Determine the quadrant of a point function quad ( p ) { if ( p [ 0 ] >= 0 && p [ 1 ] >= 0 ) return 1 ; if ( p [ 0 ] <= 0 && p [ 1 ] >= 0 ) return 2 ; if ( p [ 0 ] <= 0 && p [ 1 ] <= 0 ) return 3 ; return 4 ; } // Find orientation of triplet (a b c) function orientation ( a b c ) { let res = ( b [ 1 ] - a [ 1 ]) * ( c [ 0 ] - b [ 0 ]) - ( c [ 1 ] - b [ 1 ]) * ( b [ 0 ] - a [ 0 ]); if ( res === 0 ) return 0 ; return res > 0 ? 1 : - 1 ; } // Compare two points based on mid function compare ( p1 p2 mid ) { let p = [ p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ]]; let q = [ p2 [ 0 ] - mid [ 0 ] p2 [ 1 ] - mid [ 1 ]]; let quadP = quad ( p ); let quadQ = quad ( q ); if ( quadP !== quadQ ) return quadP - quadQ ; return ( p [ 1 ] * q [ 0 ]) - ( q [ 1 ] * p [ 0 ]); } // Sort polygon points counter-clockwise function sortPoints ( polygon ) { let n = polygon . length ; let mid = [ 0 0 ]; for ( let i = 0 ; i < n ; i ++ ) { mid [ 0 ] += polygon [ i ][ 0 ]; mid [ 1 ] += polygon [ i ][ 1 ]; polygon [ i ][ 0 ] *= n ; polygon [ i ][ 1 ] *= n ; } polygon . sort (( p1 p2 ) => compare ( p1 p2 mid )); for ( let i = 0 ; i < n ; i ++ ) { polygon [ i ][ 0 ] = Math . floor ( polygon [ i ][ 0 ] / n ); polygon [ i ][ 1 ] = Math . floor ( polygon [ i ][ 1 ] / n ); } return polygon ; } // Find upper tangent between two convex polygons function findUpperTangent ( a b ) { let n1 = a . length ; let n2 = b . length ; let maxa = - Infinity ; for ( let i = 0 ; i < n1 ; i ++ ) maxa = Math . max ( maxa a [ i ][ 0 ]); let minb = Infinity ; for ( let i = 0 ; i < n2 ; i ++ ) minb = Math . min ( minb b [ i ][ 0 ]); a = sortPoints ( a ); b = sortPoints ( b ); if ( minb < maxa ) { let temp = a ; a = b ; b = temp ; n1 = a . length ; n2 = b . length ; } let ia = 0 ib = 0 ; for ( let i = 1 ; i < n1 ; i ++ ) if ( a [ i ][ 0 ] > a [ ia ][ 0 ]) ia = i ; for ( let i = 1 ; i < n2 ; i ++ ) if ( b [ i ][ 0 ] < b [ ib ][ 0 ]) ib = i ; let inda = ia indb = ib ; let done = false ; while ( ! done ) { done = true ; while ( orientation ( b [ indb ] a [ inda ] a [( inda + 1 ) % n1 ]) > 0 ) inda = ( inda + 1 ) % n1 ; while ( orientation ( a [ inda ] b [ indb ] b [( n2 + indb - 1 ) % n2 ]) < 0 ) { indb = ( n2 + indb - 1 ) % n2 ; done = false ; } } return [ a [ inda ] b [ indb ]]; } // Driver code let a = [[ 2 2 ][ 3 1 ][ 3 3 ][ 5 2 ][ 4 0 ]]; let b = [[ 0 1 ][ 1 0 ][ 0 - 2 ][ - 1 0 ]]; let tangent = findUpperTangent ( a b ); for ( let point of tangent ) { console . log ( point [ 0 ] + ' ' + point [ 1 ]); }
Sortir
upper tangent (01) (33)
Complexité temporelle : O(n1 journal (n1) + n2 journal(n2))
Espace auxiliaire : O(1)