Avkodare

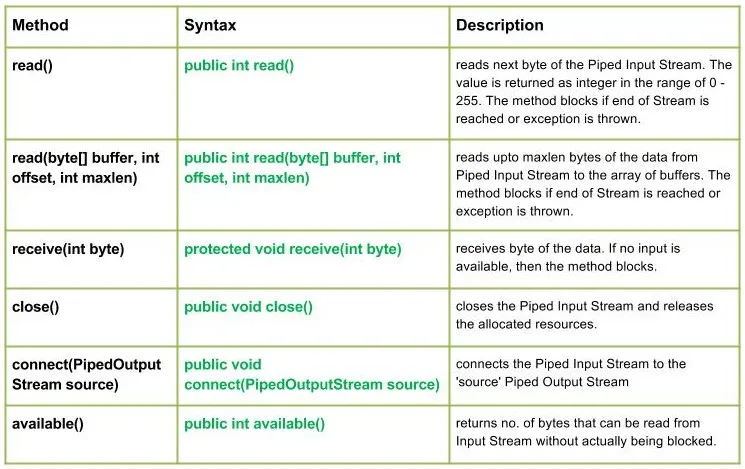
Kombinationskretsen som ändrar den binära informationen till 2 N utgångslinjer kallas Avkodare. Den binära informationen skickas i form av N inmatningslinjer. Utgångslinjerna definierar 2 N -bitkod för den binära informationen. Med enkla ord, den Avkodare utför den omvända operationen av Encoder . I taget är endast en ingångslinje aktiverad för enkelhetens skull. Den producerade 2 N -bitars utdatakod är ekvivalent med den binära informationen.

Det finns olika typer av avkodare som är följande:
2 till 4 rads avkodare:
I 2 till 4 linjers avkodare finns det totalt tre ingångar, dvs A 0 , och A 1 och E och fyra utgångar, dvs Y 0 , OCH 1 , OCH 2 , och Y 3 . För varje kombination av ingångar, när aktiveringen 'E' är inställd på 1, kommer en av dessa fyra utgångar att vara 1. Blockschemat och sanningstabellen för 2 till 4 linjers avkodare ges nedan.
Blockdiagram:

Sanningstabell:

Det logiska uttrycket för termen Y0, Y0, Y2 och Y3 är som följer:
OCH 3 =E.A 1 .A 0
OCH 2 =E.A 1 .A 0 '
OCH 1 =E.A 1 '.A 0
Y0=E.A 1 '.A 0 '
Den logiska kretsen av ovanstående uttryck ges nedan:

3 till 8 rads avkodare:
3 till 8 linjers avkodare är också känd som Binär till oktal avkodare . I en 3 till 8 linjers avkodare finns det totalt åtta utgångar, dvs Y 0 , OCH 1 , OCH 2 , OCH 3 , OCH 4 , OCH 5 , OCH 6 , och Y 7 och tre utgångar, dvs A 0 , A1 och A 2 . Denna krets har en aktiveringsingång 'E'. Precis som 2 till 4 rads avkodare, när aktiverings 'E' är inställd på 1, kommer en av dessa fyra utgångar att vara 1. Blockschemat och sanningstabellen för 3 till 8 linjers kodare ges nedan.
Blockdiagram:

Sanningstabell:

Det logiska uttrycket för termen Y 0 , OCH 1 , OCH 2 , OCH 3 , OCH 4 , OCH 5 , OCH 6 , och Y 7 enligt följande:
OCH 0 =A 0 '.A 1 '.A 2 '
OCH 1 =A 0 .A 1 '.A 2 '
OCH 2 =A 0 '.A 1 .A 2 '
OCH 3 =A 0 .A 1 .A 2 '
OCH 4 =A 0 '.A 1 '.A 2
OCH 5 =A 0 .A 1 '.A 2
OCH 6 =A 0 '.A 1 .A 2
OCH 7 =A 0 .A 1 .A 2
Den logiska kretsen av ovanstående uttryck ges nedan:

4 till 16 rader avkodare
I 4 till 16 linjers avkodare finns det totalt 16 utgångar, dvs Y 0 , OCH 1 , OCH 2 ,……, OCH 16 och fyra ingångar, dvs A 0 , A1, A 2 , och A 3 . 3 till 16 linjers avkodare kan konstrueras med antingen 2 till 4 dekoder eller 3 till 8 dekoder. Följande formel används för att hitta det nödvändiga antalet avkodare av lägre ordning.
Erforderligt antal lägre ordningens dekodrar=m 2 /m 1
m 1 = 8
m 2 = 16
Nödvändigt antal 3 till 8 avkodare=  =2
=2
Blockdiagram:

Sanningstabell:

Det logiska uttrycket för termen A0, A1, A2,..., A15 är som följer:
OCH 0 =A 0 '.A 1 '.A 2 '.A 3 '
OCH 1 =A 0 '.A 1 '.A 2 '.A 3
OCH 2 =A 0 '.A 1 '.A 2 .A 3 '
OCH 3 =A 0 '.A 1 '.A 2 .A 3
OCH 4 =A 0 '.A 1 .A 2 '.A 3 '
OCH 5 =A 0 '.A 1 .A 2 '.A 3
OCH 6 =A 0 '.A 1 .A 2 .A 3 '
OCH 7 =A 0 '.A 1 .A 2 .A 3
OCH 8 =A 0 .A 1 '.A 2 '.A 3 '
OCH 9 =A 0 .A 1 '.A 2 '.A 3
OCH 10 =A 0 .A 1 '.A 2 .A 3 '
OCH elva =A 0 .A 1 '.A 2 .A 3
OCH 12 =A 0 .A 1 .A 2 '.A 3 '
OCH 13 =A 0 .A 1 .A 2 '.A 3
OCH 14 =A 0 .A 1 .A 2 .A 3 '
OCH femton =A 0 .A 1 .A 2 '.A 3
Den logiska kretsen av ovanstående uttryck ges nedan: