PROBLEM LENEGA GOSTINCA

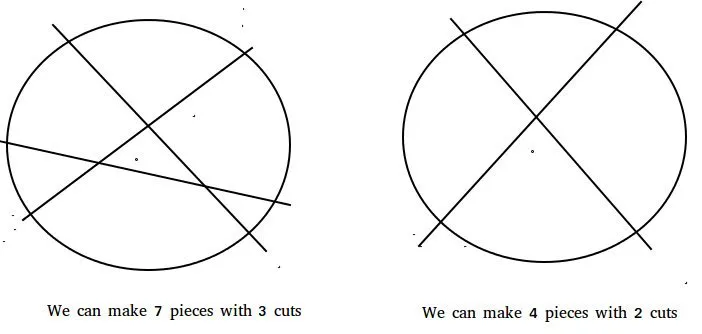
Glede na to, da je celo število, ki označuje število rezov, ki jih je mogoče narediti na palačinki, poiščite največje število kosov, ki jih je mogoče oblikovati z izdelavo N rezov.
Primeri:

Input : n = 1 Output : 2 With 1 cut we can divide the pancake in 2 pieces Input : 2 Output : 4 With 2 cuts we can divide the pancake in 4 pieces Input : 3 Output : 7 We can divide the pancake in 7 parts with 3 cuts Input : 50 Output : 1276

Priporočena praksa Problem lenega gostinca Poskusite!

Let f(n) denote the maximum number of pieces that can be obtained by making n cuts. Trivially f(0) = 1 As there'd be only 1 piece without any cut. Similarly f(1) = 2 Proceeding in similar fashion we can deduce the recursive nature of the function. The function can be represented recursively as :   f(n) = n + f(n-1)   Hence a simple solution based on the above formula can run in O(n).

Lahko optimiziramo zgornjo formulo.

We now know  f(n) = n + f(n-1) Expanding f(n-1) and so on we have  f(n) = n + n-1 + n-2 + ...... + 1 + f(0) which gives f(n) = (n*(n+1))/2 + 1

Zato lahko s to optimizacijo odgovorimo na vse poizvedbe v O (1).
Spodaj je izvedba zgornje ideje:

C++

    // A C++ program to find the solution to   // The Lazy Caterer's Problem   #include          using     namespace     std  ;   // This function receives an integer n   // and returns the maximum number of   // pieces that can be made form pancake   // using n cuts   int     findPieces  (  int     n  )   {      // Use the formula      return     (  n     *     (     n     +     1  ))     /     2     +     1  ;   }   // Driver Code   int     main  ()   {      cout      < <     findPieces  (  1  )      < <     endl  ;      cout      < <     findPieces  (  2  )      < <     endl  ;      cout      < <     findPieces  (  3  )      < <     endl  ;      cout      < <     findPieces  (  50  )      < <     endl  ;      return     0  ;   }

Java

    // Java program to find the solution to   // The Lazy Caterer's Problem   import     java.io.*  ;   class   GFG      {      // This function returns the maximum       // number of pieces that can be made      // form pancake using n cuts      static     int     findPieces  (  int     n  )      {      // Use the formula      return     (  n     *     (  n     +     1  ))     /     2     +     1  ;      }          // Driver program to test above function      public     static     void     main     (  String  []     args  )         {      System  .  out  .  println  (  findPieces  (  1  ));      System  .  out  .  println  (  findPieces  (  2  ));      System  .  out  .  println  (  findPieces  (  3  ));      System  .  out  .  println  (  findPieces  (  50  ));      }   }   // This code is contributed by Pramod Kumar

Python3

    # A Python 3 program to    # find the solution to   # The Lazy Caterer's Problem   # This function receives an    # integer n and returns the    # maximum number of pieces    # that can be made form    # pancake using n cuts   def   findPieces  (   n   ):   # Use the formula   return   (  n   *   (   n   +   1  ))   //   2   +   1   # Driver Code   print  (  findPieces  (  1  ))   print  (  findPieces  (  2  ))   print  (  findPieces  (  3  ))   print  (  findPieces  (  50  ))   # This code is contributed   # by ihritik

    // C# program to find the solution    // to The Lazy Caterer's Problem   using     System  ;   class     GFG      {      // This function returns the maximum       // number of pieces that can be made      // form pancake using n cuts      static     int     findPieces  (  int     n  )      {      // Use the formula      return     (  n     *     (  n     +     1  ))     /     2     +     1  ;      }          // Driver code      public     static     void     Main     ()         {      Console  .  WriteLine  (  findPieces  (  1  ));      Console  .  WriteLine  (  findPieces  (  2  ));      Console  .  WriteLine  (  findPieces  (  3  ));      Console  .  Write  (  findPieces  (  50  ));      }   }   // This code is contributed by Nitin Mittal.

PHP

       // A php program to find    // the solution to The    // Lazy Caterer's Problem   // This function receives    // an integer n and returns    // the maximum number of   // pieces that can be made    // form pancake using n cuts   function   findPieces  (  $n  )   {   // Use the formula   return   (  $n   *   (   $n   +   1  ))   /   2   +   1  ;   }   // Driver Code   echo   findPieces  (  1  )      '  n  '   ;   echo   findPieces  (  2  )      '  n  '   ;   echo   findPieces  (  3  )      '  n  '   ;   echo   findPieces  (  50  )     '  n  '  ;   // This code is contributed   // by nitin mittal.    ?>

JavaScript

     <  script  >   // Javascript program to find the solution to   // The Lazy Caterer's Problem      // This function returns the maximum       // number of pieces that can be made      // form pancake using n cuts      function     findPieces  (  n  )      {      // Use the formula      return     (  n     *     (  n     +     1  ))     /     2     +     1  ;      }       // Driver Code          document  .  write  (  findPieces  (  1  )     +     '  
'  );      document  .  write  (  findPieces  (  2  )     +     '  
'  );      document  .  write  (  findPieces  (  3  )     +     '  
'  );      document  .  write  (  findPieces  (  50  ));        <  /script>