Algoritem za obratno brisanje za minimalno vpeto drevo

 #practiceLinkDiv { display: none !important; }
#practiceLinkDiv { display: none !important; } Algoritem povratnega brisanja je tesno povezan z Kruskalov algoritem . V Kruskalovem algoritmu naredimo naslednje: Razvrstimo robove po naraščajočem vrstnem redu njihovih uteži. Po sortiranju enega za drugim izbiramo robove v naraščajočem vrstnem redu. Trenutno izbrani rob vključimo, če z vključitvijo tega v vpeto drevo ne tvorimo nobenega cikla, dokler v vpetem drevesu ni robov V-1, kjer je V = število vozlišč.
V algoritmu Reverse Delete razvrstimo vse robove zmanjševanje vrstni red njihovih uteži. Po razvrščanju enega za drugim izbiramo robove v padajočem vrstnem redu. mi vključi trenutno izbrani rob, če izključitev trenutnega roba povzroči prekinitev povezave v trenutnem grafu . Glavna ideja je izbrisati rob, če njegov izbris ne povzroči prekinitve povezave grafa.
Algoritem:
- Razvrsti vse robove grafa v nenaraščajočem vrstnem redu uteži robov.
- Inicializirajte MST kot izvirni graf in s 3. korakom odstranite dodatne robove.
- Izberite najtežji rob izmed preostalih robov in preverite, ali brisanje roba prekine povezavo grafa ali ne .
Če prekine povezavo, roba ne izbrišemo.
Sicer izbrišemo rob in nadaljujemo.
Ilustracija:
Naj razumemo z naslednjim primerom:
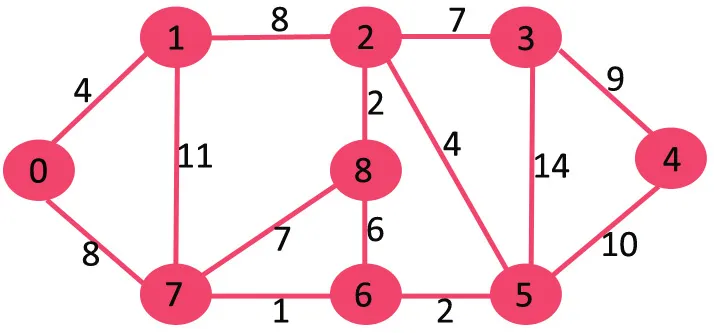
Če izbrišemo najvišji rob teže 14, graf ne postane nepovezan, zato ga odstranimo.
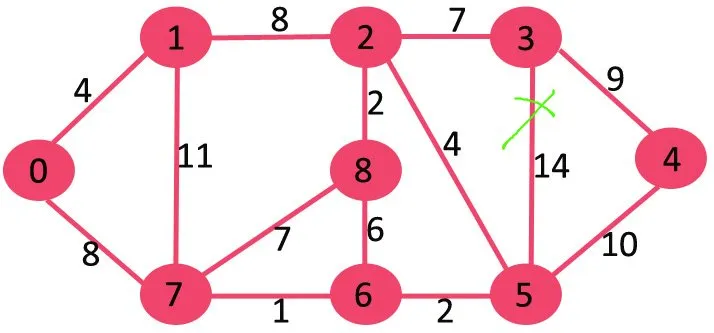
Nato izbrišemo 11, saj brisanje ne prekine povezave z grafom.
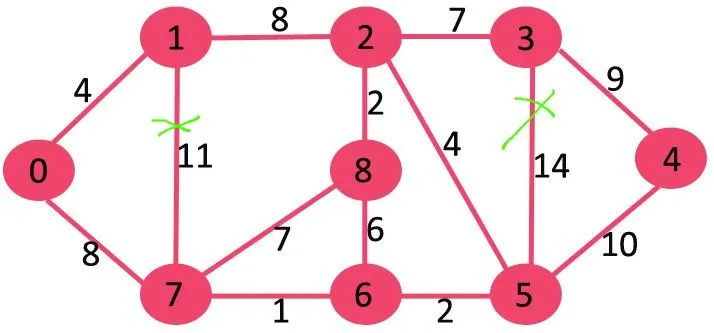
Nato izbrišemo 10, saj brisanje ne prekine povezave z grafom.

Naslednji je 9. Ne moremo izbrisati 9, saj brisanje povzroči prekinitev povezave.

Nadaljujemo po tej poti in naslednji robovi ostanejo v končnem MST.
Edges in MST
(3 4)
(0 7)
(2 3)
(2 5)
(0 1)
(5 6)
(2 8)
(6 7)
Opomba: V primeru enako težkih robov lahko izberemo kateri koli rob enakih težkih robov.
Priporočena praksa Algoritem za obratno brisanje za minimalno vpeto drevo Poskusite!Izvedba:
C++Java// C++ program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm #includeusing namespace std ; // Creating shortcut for an integer pair typedef pair < int int > iPair ; // Graph class represents a directed graph // using adjacency list representation class Graph { int V ; // No. of vertices list < int > * adj ; vector < pair < int iPair > > edges ; void DFS ( int v bool visited []); public : Graph ( int V ); // Constructor // function to add an edge to graph void addEdge ( int u int v int w ); // Returns true if graph is connected bool isConnected (); void reverseDeleteMST (); }; Graph :: Graph ( int V ) { this -> V = V ; adj = new list < int > [ V ]; } void Graph :: addEdge ( int u int v int w ) { adj [ u ]. push_back ( v ); // Add w to v’s list. adj [ v ]. push_back ( u ); // Add w to v’s list. edges . push_back ({ w { u v }}); } void Graph :: DFS ( int v bool visited []) { // Mark the current node as visited and print it visited [ v ] = true ; // Recur for all the vertices adjacent to // this vertex list < int >:: iterator i ; for ( i = adj [ v ]. begin (); i != adj [ v ]. end (); ++ i ) if ( ! visited [ * i ]) DFS ( * i visited ); } // Returns true if given graph is connected else false bool Graph :: isConnected () { bool visited [ V ]; memset ( visited false sizeof ( visited )); // Find all reachable vertices from first vertex DFS ( 0 visited ); // If set of reachable vertices includes all // return true. for ( int i = 1 ; i < V ; i ++ ) if ( visited [ i ] == false ) return false ; return true ; } // This function assumes that edge (u v) // exists in graph or not void Graph :: reverseDeleteMST () { // Sort edges in increasing order on basis of cost sort ( edges . begin () edges . end ()); int mst_wt = 0 ; // Initialize weight of MST cout < < 'Edges in MST n ' ; // Iterate through all sorted edges in // decreasing order of weights for ( int i = edges . size () -1 ; i >= 0 ; i -- ) { int u = edges [ i ]. second . first ; int v = edges [ i ]. second . second ; // Remove edge from undirected graph adj [ u ]. remove ( v ); adj [ v ]. remove ( u ); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if ( isConnected () == false ) { adj [ u ]. push_back ( v ); adj [ v ]. push_back ( u ); // This edge is part of MST cout < < '(' < < u < < ' ' < < v < < ') n ' ; mst_wt += edges [ i ]. first ; } } cout < < 'Total weight of MST is ' < < mst_wt ; } // Driver code int main () { // create the graph given in above figure int V = 9 ; Graph g ( V ); // making above shown graph g . addEdge ( 0 1 4 ); g . addEdge ( 0 7 8 ); g . addEdge ( 1 2 8 ); g . addEdge ( 1 7 11 ); g . addEdge ( 2 3 7 ); g . addEdge ( 2 8 2 ); g . addEdge ( 2 5 4 ); g . addEdge ( 3 4 9 ); g . addEdge ( 3 5 14 ); g . addEdge ( 4 5 10 ); g . addEdge ( 5 6 2 ); g . addEdge ( 6 7 1 ); g . addEdge ( 6 8 6 ); g . addEdge ( 7 8 7 ); g . reverseDeleteMST (); return 0 ; } Python3// Java program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm import java.util.* ; // class to represent an edge class Edge implements Comparable < Edge > { int u v w ; Edge ( int u int v int w ) { this . u = u ; this . w = w ; this . v = v ; } public int compareTo ( Edge other ) { return ( this . w - other . w ); } } // Class to represent a graph using adjacency list // representation public class GFG { private int V ; // No. of vertices private List < Integer >[] adj ; private List < Edge > edges ; @SuppressWarnings ({ 'unchecked' 'deprecated' }) public GFG ( int v ) // Constructor { V = v ; adj = new ArrayList [ v ] ; for ( int i = 0 ; i < v ; i ++ ) adj [ i ] = new ArrayList < Integer > (); edges = new ArrayList < Edge > (); } // function to Add an edge public void AddEdge ( int u int v int w ) { adj [ u ] . add ( v ); // Add w to v’s list. adj [ v ] . add ( u ); // Add w to v’s list. edges . add ( new Edge ( u v w )); } // function to perform dfs private void DFS ( int v boolean [] visited ) { // Mark the current node as visited and print it visited [ v ] = true ; // Recur for all the vertices adjacent to // this vertex for ( int i : adj [ v ] ) { if ( ! visited [ i ] ) DFS ( i visited ); } } // Returns true if given graph is connected else false private boolean IsConnected () { boolean [] visited = new boolean [ V ] ; // Find all reachable vertices from first vertex DFS ( 0 visited ); // If set of reachable vertices includes all // return true. for ( int i = 1 ; i < V ; i ++ ) { if ( visited [ i ] == false ) return false ; } return true ; } // This function assumes that edge (u v) // exists in graph or not public void ReverseDeleteMST () { // Sort edges in increasing order on basis of cost Collections . sort ( edges ); int mst_wt = 0 ; // Initialize weight of MST System . out . println ( 'Edges in MST' ); // Iterate through all sorted edges in // decreasing order of weights for ( int i = edges . size () - 1 ; i >= 0 ; i -- ) { int u = edges . get ( i ). u ; int v = edges . get ( i ). v ; // Remove edge from undirected graph adj [ u ] . remove ( adj [ u ] . indexOf ( v )); adj [ v ] . remove ( adj [ v ] . indexOf ( u )); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if ( IsConnected () == false ) { adj [ u ] . add ( v ); adj [ v ] . add ( u ); // This edge is part of MST System . out . println ( '(' + u + ' ' + v + ')' ); mst_wt += edges . get ( i ). w ; } } System . out . println ( 'Total weight of MST is ' + mst_wt ); } // Driver code public static void main ( String [] args ) { // create the graph given in above figure int V = 9 ; GFG g = new GFG ( V ); // making above shown graph g . AddEdge ( 0 1 4 ); g . AddEdge ( 0 7 8 ); g . AddEdge ( 1 2 8 ); g . AddEdge ( 1 7 11 ); g . AddEdge ( 2 3 7 ); g . AddEdge ( 2 8 2 ); g . AddEdge ( 2 5 4 ); g . AddEdge ( 3 4 9 ); g . AddEdge ( 3 5 14 ); g . AddEdge ( 4 5 10 ); g . AddEdge ( 5 6 2 ); g . AddEdge ( 6 7 1 ); g . AddEdge ( 6 8 6 ); g . AddEdge ( 7 8 7 ); g . ReverseDeleteMST (); } } // This code is contributed by Prithi_DeyC## Python3 program to find Minimum Spanning Tree # of a graph using Reverse Delete Algorithm # Graph class represents a directed graph # using adjacency list representation class Graph : def __init__ ( self v ): # No. of vertices self . v = v self . adj = [ 0 ] * v self . edges = [] for i in range ( v ): self . adj [ i ] = [] # function to add an edge to graph def addEdge ( self u : int v : int w : int ): self . adj [ u ] . append ( v ) # Add w to v’s list. self . adj [ v ] . append ( u ) # Add w to v’s list. self . edges . append (( w ( u v ))) def dfs ( self v : int visited : list ): # Mark the current node as visited and print it visited [ v ] = True # Recur for all the vertices adjacent to # this vertex for i in self . adj [ v ]: if not visited [ i ]: self . dfs ( i visited ) # Returns true if graph is connected # Returns true if given graph is connected else false def connected ( self ): visited = [ False ] * self . v # Find all reachable vertices from first vertex self . dfs ( 0 visited ) # If set of reachable vertices includes all # return true. for i in range ( 1 self . v ): if not visited [ i ]: return False return True # This function assumes that edge (u v) # exists in graph or not def reverseDeleteMST ( self ): # Sort edges in increasing order on basis of cost self . edges . sort ( key = lambda a : a [ 0 ]) mst_wt = 0 # Initialize weight of MST print ( 'Edges in MST' ) # Iterate through all sorted edges in # decreasing order of weights for i in range ( len ( self . edges ) - 1 - 1 - 1 ): u = self . edges [ i ][ 1 ][ 0 ] v = self . edges [ i ][ 1 ][ 1 ] # Remove edge from undirected graph self . adj [ u ] . remove ( v ) self . adj [ v ] . remove ( u ) # Adding the edge back if removing it # causes disconnection. In this case this # edge becomes part of MST. if self . connected () == False : self . adj [ u ] . append ( v ) self . adj [ v ] . append ( u ) # This edge is part of MST print ( '( %d %d )' % ( u v )) mst_wt += self . edges [ i ][ 0 ] print ( 'Total weight of MST is' mst_wt ) # Driver Code if __name__ == '__main__' : # create the graph given in above figure V = 9 g = Graph ( V ) # making above shown graph g . addEdge ( 0 1 4 ) g . addEdge ( 0 7 8 ) g . addEdge ( 1 2 8 ) g . addEdge ( 1 7 11 ) g . addEdge ( 2 3 7 ) g . addEdge ( 2 8 2 ) g . addEdge ( 2 5 4 ) g . addEdge ( 3 4 9 ) g . addEdge ( 3 5 14 ) g . addEdge ( 4 5 10 ) g . addEdge ( 5 6 2 ) g . addEdge ( 6 7 1 ) g . addEdge ( 6 8 6 ) g . addEdge ( 7 8 7 ) g . reverseDeleteMST () # This code is contributed by # sanjeev2552JavaScript// C# program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm using System ; using System.Collections.Generic ; // class to represent an edge public class Edge : IComparable < Edge > { public int u v w ; public Edge ( int u int v int w ) { this . u = u ; this . v = v ; this . w = w ; } public int CompareTo ( Edge other ) { return this . w . CompareTo ( other . w ); } } // Graph class represents a directed graph // using adjacency list representation public class Graph { private int V ; // No. of vertices private List < int > [] adj ; private List < Edge > edges ; public Graph ( int v ) // Constructor { V = v ; adj = new List < int > [ v ]; for ( int i = 0 ; i < v ; i ++ ) adj [ i ] = new List < int > (); edges = new List < Edge > (); } // function to Add an edge public void AddEdge ( int u int v int w ) { adj [ u ]. Add ( v ); // Add w to v’s list. adj [ v ]. Add ( u ); // Add w to v’s list. edges . Add ( new Edge ( u v w )); } // function to perform dfs private void DFS ( int v bool [] visited ) { // Mark the current node as visited and print it visited [ v ] = true ; // Recur for all the vertices adjacent to // this vertex foreach ( int i in adj [ v ]) { if ( ! visited [ i ]) DFS ( i visited ); } } // Returns true if given graph is connected else false private bool IsConnected () { bool [] visited = new bool [ V ]; // Find all reachable vertices from first vertex DFS ( 0 visited ); // If set of reachable vertices includes all // return true. for ( int i = 1 ; i < V ; i ++ ) { if ( visited [ i ] == false ) return false ; } return true ; } // This function assumes that edge (u v) // exists in graph or not public void ReverseDeleteMST () { // Sort edges in increasing order on basis of cost edges . Sort (); int mst_wt = 0 ; // Initialize weight of MST Console . WriteLine ( 'Edges in MST' ); // Iterate through all sorted edges in // decreasing order of weights for ( int i = edges . Count - 1 ; i >= 0 ; i -- ) { int u = edges [ i ]. u ; int v = edges [ i ]. v ; // Remove edge from undirected graph adj [ u ]. Remove ( v ); adj [ v ]. Remove ( u ); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if ( IsConnected () == false ) { adj [ u ]. Add ( v ); adj [ v ]. Add ( u ); // This edge is part of MST Console . WriteLine ( '({0} {1})' u v ); mst_wt += edges [ i ]. w ; } } Console . WriteLine ( 'Total weight of MST is {0}' mst_wt ); } } class GFG { // Driver code static void Main ( string [] args ) { // create the graph given in above figure int V = 9 ; Graph g = new Graph ( V ); // making above shown graph g . AddEdge ( 0 1 4 ); g . AddEdge ( 0 7 8 ); g . AddEdge ( 1 2 8 ); g . AddEdge ( 1 7 11 ); g . AddEdge ( 2 3 7 ); g . AddEdge ( 2 8 2 ); g . AddEdge ( 2 5 4 ); g . AddEdge ( 3 4 9 ); g . AddEdge ( 3 5 14 ); g . AddEdge ( 4 5 10 ); g . AddEdge ( 5 6 2 ); g . AddEdge ( 6 7 1 ); g . AddEdge ( 6 8 6 ); g . AddEdge ( 7 8 7 ); g . ReverseDeleteMST (); } } // This code is contributed by cavi4762
IzhodEdges in MST (3 4) (0 7) (2 3) (2 5) (0 1) (5 6) (2 8) (6 7) Total weight of MST is 37Časovna zahtevnost: O((E*(V+E)) + E log E) kjer je E število robov.
Zahtevnost prostora: O(V+E) kjer je V število oglišč in E število robov. Za shranjevanje grafa uporabljamo seznam sosednosti, zato potrebujemo prostor, sorazmeren z O(V+E).
Opombe:
- Zgornja izvedba je preprosta/naivna izvedba algoritma Reverse Delete in jo je mogoče optimizirati na O(E log V (log log V) 3 ) [Vir: en teden ]. Toda ta optimizirana časovna kompleksnost je še vedno manjša od Prim in Kruskal Algoritmi za MST.
- Zgornja izvedba spremeni prvotni graf. Ustvarimo lahko kopijo grafa, če je treba obdržati originalni graf.
Ustvari kviz