Predpogoj: Kazalci Uvod

Razmislite o naslednjem programu:

C

#include> int> main()> {> > int> arr[5] = { 1, 2, 3, 4, 5 };> > int> *ptr = arr;> > printf> (> '%p '> , ptr);> > return> 0;> }>

V zgornjem programu imamo kazalec ptr ki kaže na 0 ^th element matrike. Podobno lahko deklariramo tudi kazalec, ki lahko kaže na celotno matriko namesto le na en element matrike. Ta kazalec je uporaben, ko govorimo o večdimenzionalnih nizih.

Sintaksa:

data_type  (* var_name ) [size_of_array]; 

Tukaj:

data_type je vrsta podatkov, ki jih vsebuje matrika. var_name je ime spremenljivke kazalca. size_of_array je velikost matrike, na katero bo pokazal kazalec.

Primer

int (*ptr)[10]; 

Tukaj ptr je kazalec, ki lahko kaže na niz 10 celih števil. Ker ima indeks višjo prednost kot posrednost, je treba posredni operator in ime kazalca zapreti v oklepajih. Tukaj je tip ptr 'kazalec na niz 10 celih števil.

Opomba: Kazalec, ki kaže na 0 ^th element matrike in kazalec, ki kaže na celotno matriko, sta popolnoma različna. To prikazuje naslednji program:

C

// C program to understand difference between> // pointer to an integer and pointer to an> // array of integers.> #include> int> main()> {> > // Pointer to an integer> > int> *p;> > > // Pointer to an array of 5 integers> > int> (*ptr)[5];> > int> arr[5];> > > // Points to 0th element of the arr.> > p = arr;> > > // Points to the whole array arr.> > ptr = &arr;> > > printf> (> 'p = %p, ptr = %p '> , p, ptr);> > > p++;> > ptr++;> > > printf> (> 'p = %p, ptr = %p '> , p, ptr);> > > return> 0;> }>

Izhod

p = 0x7fff6463e890, ptr = 0x7fff6463e890 p = 0x7fff6463e894, ptr = 0x7fff6463e8a4 

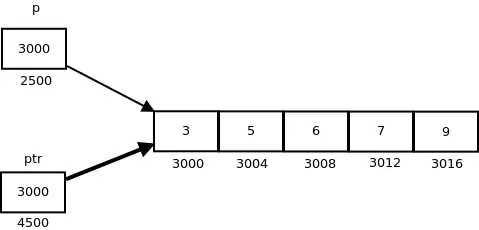
tukaj, str je kazalec na 0 ^th element matrike prir , medtem ptr je kazalec, ki kaže na celotno matriko prir .

• Osnovna vrsta str je osnovni tip int while ptr je 'niz 5 celih števil'.
• Vemo, da se aritmetika kazalca izvaja glede na osnovno velikost, tako da če napišemo ptr++, potem kazalec ptr bo pomaknjen naprej za 20 bajtov.

Naslednja slika prikazuje kazalec p in ptr. Temnejša puščica označuje kazalec na polje.

Pri dereferenciranju izraza kazalca dobimo vrednost, na katero kaže ta izraz kazalca. Kazalec na matriko kaže na matriko, zato bi morali pri dereferenciranju dobiti matriko, ime matrike pa označuje osnovni naslov. Kadar torej kazalec na matriko dereferenciramo, dobimo osnovni naslov matrike, na katero kaže.

C

// C program to illustrate sizes of> // pointer of array> #include> int> main()> {> > int> arr[] = { 3, 5, 6, 7, 9 };> > int> *p = arr;> > int> (*ptr)[5] = &arr;> > > printf> (> 'p = %p, ptr = %p '> , p, ptr);> > printf> (> '*p = %d, *ptr = %p '> , *p, *ptr);> > > printf> (> 'sizeof(p) = %lu, sizeof(*p) = %lu '> ,> > sizeof> (p),> sizeof> (*p));> > printf> (> 'sizeof(ptr) = %lu, sizeof(*ptr) = %lu '> ,> > sizeof> (ptr),> sizeof> (*ptr));> > return> 0;> }>

Izhod

p = 0x7fff55adbff0, ptr = 0x7fff55adbff0 *p = 3, *ptr = 0x7fff55adbff0 sizeof(p) = 8, sizeof(*p) = 4 sizeof(ptr) = 8, sizeof(*ptr) = 20 

Kazalec na večdimenzionalne nize

1. Kazalci in dvodimenzionalni nizi

V dvodimenzionalni matriki lahko do vsakega elementa dostopamo z uporabo dveh indeksov, kjer prvi indeks predstavlja številko vrstice, drugi indeks pa številko stolpca. Do elementov 2-D matrike je mogoče dostopati tudi s pomočjo kazalnega zapisa. Recimo, da je arr 2-D polje, lahko dostopamo do katerega koli elementa arr[i][j] matrike z uporabo izraza kazalca *(*(arr + i) + j) . Zdaj bomo videli, kako je mogoče izpeljati ta izraz.
Vzemimo dvodimenzionalni niz prihod[3][4] :

int arr[3][4] = { {1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12} };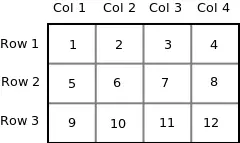 

Ker je pomnilnik v računalniku organiziran linearno, 2-D matrike ni mogoče shraniti v vrstice in stolpce. Koncept vrstic in stolpcev je le teoretičen, pravzaprav je dvodimenzionalni niz shranjen v vrstnem redu glavnih vrstic, tj. vrstice so postavljene ena poleg druge. Naslednja slika prikazuje, kako bo zgornji 2-D niz shranjen v pomnilniku.

Vsako vrstico lahko obravnavamo kot 1-D matriko, tako da lahko dvodimenzionalno matriko obravnavamo kot zbirko enodimenzionalnih matrik, ki so postavljene ena za drugo. Z drugimi besedami, lahko rečemo, da so 2-D dimenzionalni nizi, ki so postavljeni drug za drugim. Torej tukaj prir je niz 3 elementov, kjer je vsak element 1-D niz 4 celih števil.
Vemo, da je ime matrike stalni kazalec, ki kaže na 0 ^th 1-D polje in vsebuje naslov 5000. Ker prir je 'kazalec na niz 4 celih števil', glede na aritmetiko kazalca bo izraz arr + 1 predstavljal naslov 5016, izraz arr + 2 pa bo predstavljal naslov 5032.
Tako lahko rečemo prir kaže na 0 ^th 1-D niz, arr + 1 kaže na 1 ^st 1-D niz in arr + 2 kaže na 2 ^nd 1-D niz.

Na splošno lahko zapišemo:

 arr + i Points to ith element of arr ->Kaže na ith 1-D niz 

• Ker arr + i kaže na i ^th element od prir , pri dereferenciranju bo dobil i ^th element od prir ki je seveda 1-D niz. Tako izraz *(arr + i) nam daje osnovni naslov i ^th 1-D niz.
• Vemo, izraz kazalca *(arr + i) je enakovreden izrazu indeksa pride[i] . torej *(arr + i) kar je enako kot pride[i] nam daje osnovni naslov i ^th 1-D niz.
• Za dostop do posameznega elementa naše 2-D matrike bi morali imeti možnost dostopa do katerega koli j ^th element i ^th 1-D niz.
• Od osnovne vrste *(arr + i) je int in vsebuje naslov 0 ^th element i ^th 1-D polja, lahko dobimo naslove naslednjih elementov v i ^th 1-D matriko z dodajanjem celih vrednosti *(arr + i) .
• Na primer *(arr + i) + 1 bo predstavljal naslov 1 ^st element 1 ^st element i ^th 1-D niz in *(arr+i)+2 bo predstavljal naslov 2 ^nd element i ^th 1-D niz.
• Podobno bo *(arr + i) + j predstavljal naslov j ^th element i ^th 1-D niz. Pri dereferenciranju tega izraza lahko dobimo j ^th element i ^th 1-D niz.

Kazalci in tridimenzionalni nizi

int arr[2][3][2] = { {{5, 10}, {6, 11}, {7, 12}}, {{20, 30}, {21, 31}, {22, 32}} }; 

V tridimenzionalni matriki lahko do vsakega elementa dostopamo z uporabo treh indeksov. Vzemimo 3-D matriko. Tridimenzionalno matriko lahko obravnavamo kot matriko 2-D matrike, tj. vsak element 3-D matrike velja za 2-D matriko. 3-D niz prir lahko obravnavamo kot niz, sestavljen iz dveh elementov, pri čemer je vsak element 2-D niz. Ime matrike prir je kazalec na 0 ^th 2-D niz.

Tako izraz kazalca *(*(*(arr + i ) + j ) + k) je enakovreden indeksnemu izrazu arr[i][j][k].
Vemo, da je izraz *(arr + i) enakovreden arr[i] in izraz *(*(arr + i) + j) enak arr[i][j]. Tako lahko rečemo, da arr[i] predstavlja osnovni naslov i ^th 2-D polje in arr[i][j] predstavlja osnovni naslov j ^th 1-D niz.

Primer

Spodnji primer prikazuje program za tiskanje elementov 3D niza z uporabo kazalcev.

C

// C program to print the elements of 3-D> // array using pointer notation> #include> int> main()> {> > int> arr[2][3][2] = {> > {> > {5, 10},> > {6, 11},> > {7, 12},> > },> > {> > {20, 30},> > {21, 31},> > {22, 32},> > }> > };> > int> i, j, k;> > for> (i = 0; i <2; i++)> > {> > for> (j = 0; j <3; j++)> > {> > for> (k = 0; k <2; k++)> > printf> (> '%d '> , *(*(*(arr + i) + j) +k));> > printf> (> ' '> );> > }> > }> > return> 0;> }>

Izhod

5 10 6 11 7 12 20 30 21 31 22 32 

Naslednja slika prikazuje, kako je 3-D polje, uporabljeno v zgornjem programu, shranjeno v pomnilniku.

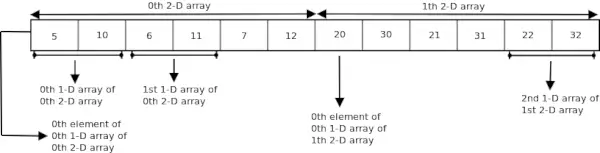
Naročanje kazalca na matriko

Recimo prir je 2-D polje s 3 vrsticami in 4 stolpci in ptr je kazalec na niz 4 celih števil in ptr vsebuje osnovni naslov matrike prir .

int arr[3][4] = {{10, 11, 12, 13}, {20, 21, 22, 23}, {30, 31, 32, 33}}; int (*ptr)[4]; ptr = arr;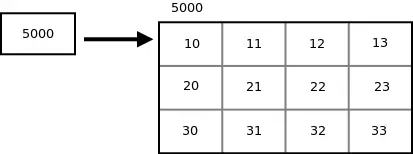 

Od ptr je kazalec na dvodimenzionalno matriko prve vrstice, tj. matriko 4 celih števil, ptr + i bo pokazal na i ^th vrstica. Pri dereferenciranju ptr + i , dobimo osnovni naslov i ^th vrstica. Za dostop do naslova j ^th element i ^th vrstici lahko izrazu kazalca dodamo j *(ptr + i) . Torej izraz kazalca *(ptr + i) + j podaja naslov j ^th element i ^th vrstica in izraz kazalca *(*(ptr + i)+j) podaja vrednost j ^th element i ^th vrstica.
Vemo, da je kazalni izraz *(*(ptr + i) + j) enakovreden indeksnemu izrazu ptr[i][j]. Torej, če imamo spremenljivko kazalca, ki vsebuje osnovni naslov 2-D matrike, potem lahko dostopamo do elementov matrike tako, da dvojno podpišemo to spremenljivko kazalca.

Primer

C

// C program to print elements of a 2-D array> // by scripting a pointer to an array> #include> int> main()> {> > int> arr[3][4] = {> > {10, 11, 12, 13},> > {20, 21, 22, 23},> > {30, 31, 32, 33}> > };> > int> (*ptr)[4];> > ptr = arr;> > printf> (> '%p %p %p '> , ptr, ptr + 1, ptr + 2);> > printf> (> '%p %p %p '> , *ptr, *(ptr + 1), *(ptr + 2));> > printf> (> '%d %d %d '> , **ptr, *(*(ptr + 1) + 2), *(*(ptr + 2) + 3));> > printf> (> '%d %d %d '> , ptr[0][0], ptr[1][2], ptr[2][3]);> > return> 0;> }>

Izhod

0x7ffc9556b790 0x7ffc9556b7a0 0x7ffc9556b7b0 0x7ffc9556b790 0x7ffc9556b7a0 0x7ffc9556b7b0 10 22 33 10 22 33