Poiščite največjo dolžino kačje zaporedje
Glede na mrežo številk poiščite največjo dolžino kačje zaporedje in ga natisnite. Če obstaja več zaporedja kače z največjo dolžino natisnite katero od njih.
Zaporedje kač je sestavljeno iz sosednjih številk v mreži, tako da je za vsako številko na desni ali številka spodaj vrednost +1 ali -1 njegova vrednost. Na primer, če ste na lokaciji (x y) v omrežju, se lahko premikate desno, tj. (X y+1), če je ta številka ± 1 ali se premaknete navzdol, tj. (X+1 y), če je ta številka ± 1.
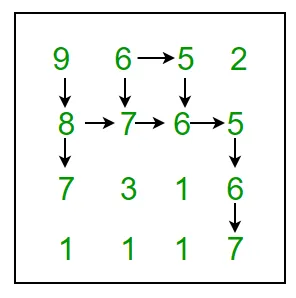
For example 9 6 5 2 8 7 6 5 7 3 1 6 1 1 1 7 In above grid the longest snake sequence is: (9 8 7 6 5 6 7)
Spodaj prikazuje vse možne poti:

Toplo vam priporočamo, da svoj brskalnik zmanjšate in to najprej preizkusite sami.
Ideja je uporaba dinamičnega programiranja. Za vsako celico matrice ohranimo največjo dolžino kače, ki se konča v trenutni celici. Zaporedje kače največje dolžine bo imelo največjo vrednost. Celica največje vrednosti bo ustrezala repu kače. Da bi kačo natisnili, se moramo vrniti z repa vse do kačje glave.
Let T[i][i] represent maximum length of a snake which ends at cell (i j) then for given matrix M the DP relation is defined as T[0][0] = 0 T[i][j] = max(T[i][j] T[i][j - 1] + 1) if M[i][j] = M[i][j - 1] ± 1 T[i][j] = max(T[i][j] T[i - 1][j] + 1) if M[i][j] = M[i - 1][j] ± 1
Spodaj je izvedba ideje
C++ // C++ program to find maximum length // Snake sequence and print it #include using namespace std ; #define M 4 #define N 4 struct Point { int x y ; }; // Function to find maximum length Snake sequence path // (i j) corresponds to tail of the snake list < Point > findPath ( int grid [ M ][ N ] int mat [ M ][ N ] int i int j ) { list < Point > path ; Point pt = { i j }; path . push_front ( pt ); while ( grid [ i ][ j ] != 0 ) { if ( i > 0 && grid [ i ][ j ] - 1 == grid [ i - 1 ][ j ]) { pt = { i - 1 j }; path . push_front ( pt ); i -- ; } else if ( j > 0 && grid [ i ][ j ] - 1 == grid [ i ][ j - 1 ]) { pt = { i j - 1 }; path . push_front ( pt ); j -- ; } } return path ; } // Function to find maximum length Snake sequence void findSnakeSequence ( int mat [ M ][ N ]) { // table to store results of subproblems int lookup [ M ][ N ]; // initialize by 0 memset ( lookup 0 sizeof lookup ); // stores maximum length of Snake sequence int max_len = 0 ; // store coordinates to snake's tail int max_row = 0 ; int max_col = 0 ; // fill the table in bottom-up fashion for ( int i = 0 ; i < M ; i ++ ) { for ( int j = 0 ; j < N ; j ++ ) { // do except for (0 0) cell if ( i || j ) { // look above if ( i > 0 && abs ( mat [ i - 1 ][ j ] - mat [ i ][ j ]) == 1 ) { lookup [ i ][ j ] = max ( lookup [ i ][ j ] lookup [ i - 1 ][ j ] + 1 ); if ( max_len < lookup [ i ][ j ]) { max_len = lookup [ i ][ j ]; max_row = i max_col = j ; } } // look left if ( j > 0 && abs ( mat [ i ][ j - 1 ] - mat [ i ][ j ]) == 1 ) { lookup [ i ][ j ] = max ( lookup [ i ][ j ] lookup [ i ][ j - 1 ] + 1 ); if ( max_len < lookup [ i ][ j ]) { max_len = lookup [ i ][ j ]; max_row = i max_col = j ; } } } } } cout < < 'Maximum length of Snake sequence is: ' < < max_len < < endl ; // find maximum length Snake sequence path list < Point > path = findPath ( lookup mat max_row max_col ); cout < < 'Snake sequence is:' ; for ( auto it = path . begin (); it != path . end (); it ++ ) cout < < endl < < mat [ it -> x ][ it -> y ] < < ' (' < < it -> x < < ' ' < < it -> y < < ')' ; } // Driver code int main () { int mat [ M ][ N ] = { { 9 6 5 2 } { 8 7 6 5 } { 7 3 1 6 } { 1 1 1 7 } }; findSnakeSequence ( mat ); return 0 ; }
Java // Java program to find maximum length // Snake sequence and print it import java.util.* ; class GFG { static int M = 4 ; static int N = 4 ; static class Point { int x y ; public Point ( int x int y ) { this . x = x ; this . y = y ; } }; // Function to find maximum length Snake sequence path // (i j) corresponds to tail of the snake static List < Point > findPath ( int grid [][] int mat [][] int i int j ) { List < Point > path = new LinkedList <> (); Point pt = new Point ( i j ); path . add ( 0 pt ); while ( grid [ i ][ j ] != 0 ) { if ( i > 0 && grid [ i ][ j ] - 1 == grid [ i - 1 ][ j ] ) { pt = new Point ( i - 1 j ); path . add ( 0 pt ); i -- ; } else if ( j > 0 && grid [ i ][ j ] - 1 == grid [ i ][ j - 1 ] ) { pt = new Point ( i j - 1 ); path . add ( 0 pt ); j -- ; } } return path ; } // Function to find maximum length Snake sequence static void findSnakeSequence ( int mat [][] ) { // table to store results of subproblems int [][] lookup = new int [ M ][ N ] ; // initialize by 0 // stores maximum length of Snake sequence int max_len = 0 ; // store coordinates to snake's tail int max_row = 0 ; int max_col = 0 ; // fill the table in bottom-up fashion for ( int i = 0 ; i < M ; i ++ ) { for ( int j = 0 ; j < N ; j ++ ) { // do except for (0 0) cell if ( i != 0 || j != 0 ) { // look above if ( i > 0 && Math . abs ( mat [ i - 1 ][ j ] - mat [ i ][ j ] ) == 1 ) { lookup [ i ][ j ] = Math . max ( lookup [ i ][ j ] lookup [ i - 1 ][ j ] + 1 ); if ( max_len < lookup [ i ][ j ] ) { max_len = lookup [ i ][ j ] ; max_row = i ; max_col = j ; } } // look left if ( j > 0 && Math . abs ( mat [ i ][ j - 1 ] - mat [ i ][ j ] ) == 1 ) { lookup [ i ][ j ] = Math . max ( lookup [ i ][ j ] lookup [ i ][ j - 1 ] + 1 ); if ( max_len < lookup [ i ][ j ] ) { max_len = lookup [ i ][ j ] ; max_row = i ; max_col = j ; } } } } } System . out . print ( 'Maximum length of Snake ' + 'sequence is: ' + max_len + 'n' ); // find maximum length Snake sequence path List < Point > path = findPath ( lookup mat max_row max_col ); System . out . print ( 'Snake sequence is:' ); for ( Point it : path ) System . out . print ( 'n' + mat [ it . x ][ it . y ] + ' (' + it . x + ' ' + it . y + ')' ); } // Driver code public static void main ( String [] args ) { int mat [][] = {{ 9 6 5 2 } { 8 7 6 5 } { 7 3 1 6 } { 1 1 1 7 }}; findSnakeSequence ( mat ); } } // This code is contributed by 29AjayKumar
C# // C# program to find maximum length // Snake sequence and print it using System ; using System.Collections.Generic ; class GFG { static int M = 4 ; static int N = 4 ; public class Point { public int x y ; public Point ( int x int y ) { this . x = x ; this . y = y ; } }; // Function to find maximum length Snake sequence path // (i j) corresponds to tail of the snake static List < Point > findPath ( int [ ] grid int [ ] mat int i int j ) { List < Point > path = new List < Point > (); Point pt = new Point ( i j ); path . Insert ( 0 pt ); while ( grid [ i j ] != 0 ) { if ( i > 0 && grid [ i j ] - 1 == grid [ i - 1 j ]) { pt = new Point ( i - 1 j ); path . Insert ( 0 pt ); i -- ; } else if ( j > 0 && grid [ i j ] - 1 == grid [ i j - 1 ]) { pt = new Point ( i j - 1 ); path . Insert ( 0 pt ); j -- ; } } return path ; } // Function to find maximum length Snake sequence static void findSnakeSequence ( int [ ] mat ) { // table to store results of subproblems int [ ] lookup = new int [ M N ]; // initialize by 0 // stores maximum length of Snake sequence int max_len = 0 ; // store coordinates to snake's tail int max_row = 0 ; int max_col = 0 ; // fill the table in bottom-up fashion for ( int i = 0 ; i < M ; i ++ ) { for ( int j = 0 ; j < N ; j ++ ) { // do except for (0 0) cell if ( i != 0 || j != 0 ) { // look above if ( i > 0 && Math . Abs ( mat [ i - 1 j ] - mat [ i j ]) == 1 ) { lookup [ i j ] = Math . Max ( lookup [ i j ] lookup [ i - 1 j ] + 1 ); if ( max_len < lookup [ i j ]) { max_len = lookup [ i j ]; max_row = i ; max_col = j ; } } // look left if ( j > 0 && Math . Abs ( mat [ i j - 1 ] - mat [ i j ]) == 1 ) { lookup [ i j ] = Math . Max ( lookup [ i j ] lookup [ i j - 1 ] + 1 ); if ( max_len < lookup [ i j ]) { max_len = lookup [ i j ]; max_row = i ; max_col = j ; } } } } } Console . Write ( 'Maximum length of Snake ' + 'sequence is: ' + max_len + 'n' ); // find maximum length Snake sequence path List < Point > path = findPath ( lookup mat max_row max_col ); Console . Write ( 'Snake sequence is:' ); foreach ( Point it in path ) Console . Write ( 'n' + mat [ it . x it . y ] + ' (' + it . x + ' ' + it . y + ')' ); } // Driver code public static void Main ( String [] args ) { int [ ] mat = { { 9 6 5 2 } { 8 7 6 5 } { 7 3 1 6 } { 1 1 1 7 } }; findSnakeSequence ( mat ); } } // This code is contributed by Princi Singh
Python3 def snakesequence ( S m n ): sequence = {} DP = [[ 1 for x in range ( m + 1 )] for x in range ( n + 1 )] a b maximum = 0 0 0 position = [ 0 0 ] for i in range ( 0 n + 1 ): for j in range ( 0 m + 1 ): a b = 0 0 p = 'initial' if ( i > 0 and abs ( S [ i ][ j ] - S [ i - 1 ][ j ]) == 1 ): a = DP [ i - 1 ][ j ] if ( j > 0 and abs ( S [ i ][ j ] - S [ i ][ j - 1 ]) == 1 ): b = DP [ i ][ j - 1 ] if a != 0 and a >= b : p = str ( i - 1 ) + ' ' + str ( j ) elif b != 0 : p = str ( i ) + ' ' + str ( j - 1 ) q = str ( i ) + ' ' + str ( j ) sequence [ q ] = p DP [ i ][ j ] = DP [ i ][ j ] + max ( a b ) if DP [ i ][ j ] >= maximum : maximum = DP [ i ][ j ] position [ 0 ] = i position [ 1 ] = j snakeValues = [] snakePositions = [] snakeValues . append ( S [ position [ 0 ]][ position [ 1 ]]) check = 'found' str_next = str ( position [ 0 ]) + ' ' + str ( position [ 1 ]) findingIndices = sequence [ str_next ] . split () while ( check == 'found' ): if sequence [ str_next ] == 'initial' : snakePositions . insert ( 0 str_next ) check = 'end' continue findingIndices = sequence [ str_next ] . split () g = int ( findingIndices [ 0 ]) h = int ( findingIndices [ 1 ]) snakeValues . insert ( 0 S [ g ][ h ]) snake_position = str ( g ) + ' ' + str ( h ) snakePositions . insert ( 0 str_next ) str_next = sequence [ str_next ] return [ snakeValues snakePositions ] S = [[ 9 6 5 2 ] [ 8 7 6 5 ] [ 7 3 1 6 ] [ 1 1 10 7 ]] m = 3 n = 3 seq = snakesequence ( S m n ) for i in range ( len ( seq [ 0 ])): print ( seq [ 0 ][ i ] '' seq [ 1 ][ i ] . split ())
JavaScript function snakesequence ( S m n ) { let sequence = {} let DP = new Array ( n + 1 ) for ( var i = 0 ; i <= n ; i ++ ) DP [ i ] = new Array ( m + 1 ). fill ( 1 ) let a = 0 b = 0 maximum = 0 let position = [ 0 0 ] for ( var i = 0 ; i <= n ; i ++ ) { for ( var j = 0 ; j <= m ; j ++ ) { a = 0 b = 0 let p = 'initial' if ( i > 0 && Math . abs ( S [ i ][ j ] - S [ i - 1 ][ j ]) == 1 ) a = DP [ i - 1 ][ j ] if ( j > 0 && Math . abs ( S [ i ][ j ] - S [ i ][ j - 1 ]) == 1 ) b = DP [ i ][ j - 1 ] if ( a != 0 && a >= b ) p = String ( i - 1 ) + ' ' + String ( j ) else if ( b != 0 ) p = String ( i ) + ' ' + String ( j - 1 ) let q = String ( i ) + ' ' + String ( j ) sequence [ q ] = p DP [ i ][ j ] = DP [ i ][ j ] + Math . max ( a b ) if ( DP [ i ][ j ] >= maximum ) { maximum = DP [ i ][ j ] position [ 0 ] = i position [ 1 ] = j } } } let snakeValues = [] let snakePositions = [] snakeValues . push ( S [ position [ 0 ]][ position [ 1 ]]) let check = 'found' let String_next = String ( position [ 0 ]) + ' ' + String ( position [ 1 ]) let findingIndices = sequence [ String_next ]. split ( ' ' ) while ( check == 'found' ) { if ( sequence [ String_next ] == 'initial' ) { snakePositions . unshift ( String_next ) check = 'end' continue } findingIndices = sequence [ String_next ]. split ( ' ' ) let g = parseInt ( findingIndices [ 0 ]) let h = parseInt ( findingIndices [ 1 ]) snakeValues . unshift ( S [ g ][ h ]) let snake_position = String ( g ) + ' ' + String ( h ) snakePositions . unshift ( String_next ) String_next = sequence [ String_next ] } return [ snakeValues snakePositions ] } // Driver Code let S = [[ 9 6 5 2 ] [ 8 7 6 5 ] [ 7 3 1 6 ] [ 1 1 10 7 ]] let m = 3 let n = 3 let seq = snakesequence ( S m n ) for ( var i = 0 ; i < seq [ 0 ]. length ; i ++ ) console . log ( seq [ 0 ][ i ] + '' seq [ 1 ][ i ]. split ( ' ' ))
Izhod
Maximum length of Snake sequence is: 6 Snake sequence is: 9 (0 0) 8 (1 0) 7 (1 1) 6 (1 2) 5 (1 3) 6 (2 3) 7 (3 3)
Časovna kompleksnost zgornje raztopine je O (M*N). Pomožni prostor, ki ga uporablja zgornja rešitev, je O (M*N). Če nam ni treba tiskati kačjega prostora, je mogoče še zmanjšati na O (n), saj rezultat uporablja samo iz zadnje vrstice.