Unit Circle: Definícia, vzorec, diagram a vyriešené príklady
Jednotková kružnica je kružnica, ktorej polomer je 1. Stred jednotkovej kružnice je v počiatku (0,0) na osi. The obvod jednotkovej kružnice je 2π jednotiek, zatiaľ čo plocha jednotkovej kružnice je π jednotiek 2 . Nesie všetky vlastnosti Circle. Jednotka Kruh má rovnicu x 2 + a 2 = 1. Tento jednotkový kruh pomáha pri definovaní rôznych trigonometrických konceptov.

Jednotkový kruh
Jednotkový kruh sa často označuje ako S 1 zovšeobecnenie do vyšších dimenzií je jednotková sféra. Pozrime sa podrobnejšie na príklady Unit Circle, Vzorec a Solved.
Čo je Unit Circle?
Unit Circle je kruh, ktorý má polomer jednej (1) jednotky. Na kreslenie jednotkovej kružnice používame kartézsku rovinu a jednotková kružnica je 2-stupňový polynóm s dvoma premennými. Jednotkový kruh má rôzne aplikácie v trigonometrii a algebre a používa sa hlavne na nájdenie hodnôt rôznych trigonometrických pomerov, ako sú sin x, cos x, tan x a iné.
Definícia kruhu jednotky
V matematike definujeme jednotkový kruh ako miesto pevného bodu, ktorý je vo vzdialenosti jednej jednotky od stredu kruhu. Jednotková kružnica má polomer jednej jednotky a preto názov jednotková kružnica.
Rovnica jednotkového kruhu
Vieme, že rovnica každého kruhu so stredom (h, k) a polomerom „r“ je,
(x – h) 2 + (y – k) 2 = r 2
Pre jednotkový kruh vieme, že r je 1 jednotka, takže rovnica jednotkového kruhu je,
(x – h) 2 + (y – k) 2 = 1
Vzorec jednotkového kruhu
Ak je stred jednotkovej kružnice počiatkom, t.j. (h, k) = (0, 0), potom rovnica jednotkovej kružnice je,
X 2 + a 2 = 1
Na obrázku nižšie je znázornený jednotkový kruh so stredovými súradnicami h, k a keď je kruh na začiatku, hodnota h a k je nula a polomer AP sa rovná 1 jednotke.
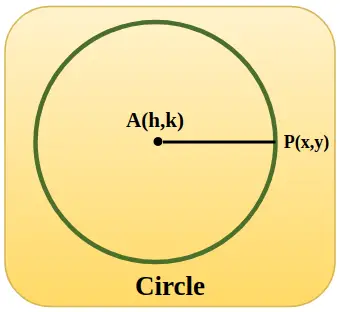
Goniometrické funkcie využívajúce jednotkový kruh
Aplikácia Pythagorovej vety v jednotkovej kružnici sa dá lepšie využiť na pochopenie goniometrických funkcií. Na tento účel považujeme pravouhlý trojuholník za umiestnený vo vnútri jednotkovej kružnice v karteziánskej súradnicovej rovine. Ak si všimneme, polomer tejto kružnice označuje preponu pravouhlého trojuholníka.
Polomer kruhu tvorí vektor. To vedie k vytvoreniu uhla, povedzme θ, s kladnou osou x. Predpokladajme, že x je základná dĺžka a y je nadmorská dĺžka pravouhlého trojuholníka. Súradnice koncových bodov polomerového vektora sú tiež (x, y).
Pravouhlý trojuholník obsahuje strany 1, x a y. Trigonometrický pomer možno teraz vypočítať takto:
sin θ = Nadmorská výška/Hypotenúza = y/1
cos θ = báza/hypotenza = x/1
teraz
- sin θ = y
- cos θ = x
- tan θ = sin θ /cos θ = y/x
Dosadením hodnôt θ môžeme získať hlavné hodnoty všetkých goniometrických funkcií. Podobne sa nachádzajú hodnoty goniometrických funkcií pri rôznych hodnotách.
Unit Circle s Sin Cos a Tan
Akýkoľvek bod na jednotkovej kružnici so súradnicami (x, y) je reprezentovaný pomocou goniometrických identít ako, (cosθ, sinθ). Súradnice rohov polomeru predstavujú kosínus a sínus hodnôt θ pre konkrétnu hodnotu θ a priamku polomeru. Máme cos θ = x a sin θ = y. Existujú štyri časti kruhu, z ktorých každá leží v jednom kvadrante a zviera uhol 90°, 180°, 270° a 360°. Hodnoty polomeru ležia medzi -1 až 1. Hodnoty sin θ a cos θ sú tiež medzi 1 a -1.
Jednotkový kruh a goniometrické identity
Trigonometrické identity jednotkového kruhu pre kotangens, sekans a kosekans možno vypočítať pomocou identít pre sin, cos a tan. Nakoniec dostaneme pravouhlý trojuholník so stranami 1, x a y. Výpočet identít jednotkového kruhu možno vyjadriť ako,
- sin θ = y/1
- cos θ = x/1
- tan θ = y/x
- sek. 0 = 1/x
- cosec 6 = 1/r
- detská postieľka θ = x/y
Jednotkový kruhový graf
Jednotkový kruhový graf je graf, ktorý obsahuje hodnotu trigonometrickej funkcie sínus a kosínus pre rôzne uhly. Jednotkový kruhový graf pre to isté je pridaný nižšie,
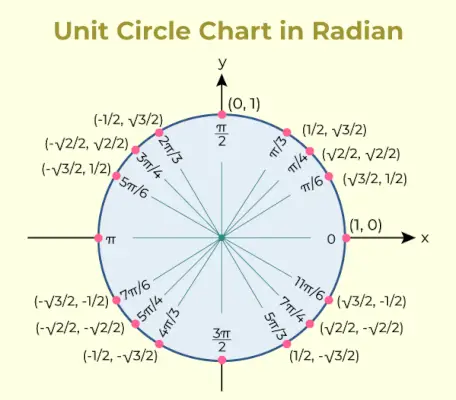
Unit Circle Table
Trigonometrické pomery použité v tabuľke jednotkových kružníc sa používajú na zoznam súradníc bodov na jednotkovej kružnici, ktoré zodpovedajú spoločným uhlom.
| Uhly | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| bez | 0 | 1/2 | 1/√ (2) | √3/2 | 1 |
| cos | 1 | √3/2 | 1/√ (2) | 1/2 | 0 |
| tak | 0 | 1/√ (3) | 1 | √ (3) | Neurčené |
| csc | Neurčené | 2 | √ (2) | 23) | 1 |
| sek | 1 | 23) | √ (2) | 2 | Neurčené |
| detská postieľka | Neurčené | √ (3) | 1 | 1/√ (3) | 0 |
Jednotkový kruh Pytagorejské identity
Existujú tri pytagorejské identity a všetky sa dajú ľahko dokázať pomocou konceptu jednotkového kruhu, ktorým sú tri pytagorejské identity,
- bez 2 θ + cos 2 θ = 1
- 1 + tak 2 θ = sek 2 i
- 1 + detská postieľka 2 θ = kosec 2 i
Jednotka Kruhová Komplexná Rovina
Komplexné čísla a komplexná rovina sa dajú ľahko vysvetliť pomocou konceptu jednotkového kruhu. Rovnica jednotkového kruhu v komplexnom tvare je,
|z| = 1
ALEBO
X 2 + a 2 = 1
V Eulerovom tvare je komplexné číslo reprezentované ako,
z = e to = náklady t + i (sin t)
Čítaj viac
Vyriešené príklady na Unit Circle
Q1: Dokážte, že bod Q leží na jednotkovej kružnici, Q = [1/√(6), √4/√6]
Riešenie:
Vzhľadom na to,
- Q = [1/√(6), √4/√6]
x = 1/√(6), y = √4/√6
Rovnica jednotkového kruhu je,
X 2 + a 2 = 1
LHS = (1/√(6)) 2 + (√4/√6) 2
LHS = 1/6 + 4/6 = 5/6 ≠ 1
LHS ≠ RHS
Bod Q[1/√(6), √4/√6] teda neleží na jednotkovej kružnici.
Q2: Vypočítajte tak 30 O pomocou hodnôt sin a cos jednotkového kruhu.
Riešenie:
opálenie 30° s použitím hodnôt sin a cos,
opálenie 30° = (sin 30°)/ (cos 30°)
- bez 30° = 1/2
- cos 30° = √(3)/2
opálenie 30° = 1/2/√(3)/2
opálenie 30° = 1/√(3)
Q3: Overte, či bod P [1/2, √(3)/2] leží na jednotkovej kružnici.
Riešenie:
Vzhľadom na to,
P = [1/2, √(3)/2]
- x = 1/2
- y = √(3)/2
Rovnica jednotkového kruhu je,
- X 2 + a 2 = 1
LHS
= (1/2) 2 + (√(3)/2) 2
= 1/4 + 3/4
= (1 + 3)/4 = 4/4
= 1
= RHS
Cvičné otázky na Unit Circle
Q1. Kontrola Ak body A (1/2, 3/2) ležia na jednotkovej kružnici.
Q2. Kontrola Ak body A (2, 1/2) ležia na jednotkovej kružnici.
Q3. Nájdite hodnotu cos 240°
Q4. Nájdite hodnotu tan 320°
Q5. Nájdite hodnotu hriechu 160°
Unit Circle – FAQ
Čo je Unit Circle?
Jednotková kružnica je definovaná ako umiestnenie bodu vo vzdialenosti jednej jednotky od pevného bodu. Má stred v (0,0) a hodnota jeho polomeru je 1.
Ako skontrolovať, či bod leží na kruhu jednotky?
Akýkoľvek bod ležiaci v 2D rovine, ktorý má tvar (x, y), je vložený do jednotkovej kružnicovej rovnice x 2 + a 2 = 1 na overenie, či leží na kruhu alebo nie.
Aký je vzorec Unit Circle?
Vzorec jednotkového kruhu je vzorec, ktorý sa používa na algebraické znázornenie jednotkového kruhu. Vzorec jednotkového kruhu je daný ako,
X 2 + a 2 = 1
Prečo sa nazýva Unit Circle?
Jednotková kružnica sa nazýva jednotková kružnica, pretože má polomer jednej (1) jednotiek.