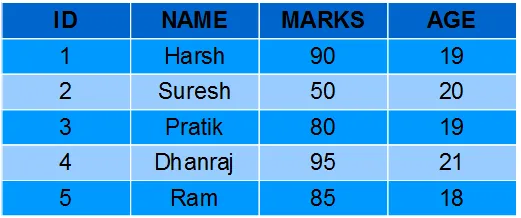
Cesta s minimálnymi nákladmi s povolenými pohybmi doľava, doprava, zdola a hore


Vzhľadom na veľkosť 2D mriežky n*n kde každá bunka predstavuje náklady na prechod cez túto bunku, úlohou je nájsť minimálne náklady presunúť sa z vľavo hore bunky k vpravo dole bunka. Z danej bunky sa môžeme nasťahovať 4 smery : zľava doprava hore dole.
Poznámka: Predpokladá sa, že vo vstupnej matici neexistujú negatívne cykly nákladov.
Príklad:
Vstup: mriežka = {{9 4 9 9}
{6 7 6 4}
{8 3 3 7}
{7 4 9 10}}
Výstup: 43
Vysvetlenie: Minimálna cena je 9 + 4 + 7 + 3 + 3 + 7 + 10.
Prístup:
Myšlienka je použiť Dijkstrov algoritmus nájsť cestu minimálnych nákladov cez sieť. Tento prístup považuje mriežku za graf, kde každá bunka je uzlom a algoritmus dynamicky skúma nákladovo najefektívnejšiu cestu k bunke vpravo dole tak, že vždy najprv rozšíri cesty s najnižšími nákladmi.
Postup krok za krokom:
- Použite mini-hromadu, aby ste vždy najskôr spracovali cestu s najnižšími nákladmi a zatlačili do nej ľavú hornú bunku.
- Inicializujte cenovú maticu s maximálnymi hodnotami nastavením ceny počiatočnej bunky na jej mriežkovú hodnotu.
- Pre každú bunku skontrolujte všetky 4 susediace bunky
- Ak sa nájde cesta s nižšími nákladmi, aktualizujte cenu bunky a vložte ju do hromady.
- Vráťte minimálnu cenu, aby ste sa dostali do bunky vpravo dole.
Nižšie je uvedená implementácia vyššie uvedeného prístupu:
C++ // C++ program to find minimum Cost Path with // Left Right Bottom and Up moves allowed #include using namespace std ; // Function to check if cell is valid. bool isValidCell ( int i int j int n ) { return i >= 0 && i < n && j >= 0 && j < n ; } int minimumCostPath ( vector < vector < int >> & grid ) { int n = grid . size (); // Min heap to implement dijkstra priority_queue < vector < int > vector < vector < int >> greater < vector < int >>> pq ; // 2d grid to store minimum cost // to reach every cell. vector < vector < int >> cost ( n vector < int > ( n INT_MAX )); cost [ 0 ][ 0 ] = grid [ 0 ][ 0 ]; // Direction vector to move in 4 directions vector < vector < int >> dir = {{ -1 0 } { 1 0 } { 0 -1 } { 0 1 }}; pq . push ({ grid [ 0 ][ 0 ] 0 0 }); while ( ! pq . empty ()) { vector < int > top = pq . top (); pq . pop (); int c = top [ 0 ] i = top [ 1 ] j = top [ 2 ]; // Check for all 4 neighbouring cells. for ( auto d : dir ) { int x = i + d [ 0 ]; int y = j + d [ 1 ]; // If cell is valid and cost to reach this cell // from current cell is less if ( isValidCell ( x y n ) && cost [ i ][ j ] + grid [ x ][ y ] < cost [ x ][ y ]) { // Update cost to reach this cell. cost [ x ][ y ] = cost [ i ][ j ] + grid [ x ][ y ]; // Push the cell into heap. pq . push ({ cost [ x ][ y ] x y }); } } } // Return minimum cost to // reach bottom right cell. return cost [ n -1 ][ n -1 ]; } int main () { vector < vector < int >> grid = {{ 9 4 9 9 }{ 6 7 6 4 }{ 8 3 3 7 }{ 7 4 9 10 }}; cout < < minimumCostPath ( grid ) < < endl ; return 0 ; }
Java // Java program to find minimum Cost Path with // Left Right Bottom and Up moves allowed import java.util.PriorityQueue ; import java.util.Arrays ; class GfG { // Function to check if cell is valid. static boolean isValidCell ( int i int j int n ) { return i >= 0 && i < n && j >= 0 && j < n ; } static int minimumCostPath ( int [][] grid ) { int n = grid . length ; // Min heap to implement Dijkstra PriorityQueue < int []> pq = new PriorityQueue <> (( a b ) -> Integer . compare ( a [ 0 ] b [ 0 ] )); // 2D grid to store minimum cost // to reach every cell. int [][] cost = new int [ n ][ n ] ; for ( int [] row : cost ) { Arrays . fill ( row Integer . MAX_VALUE ); } cost [ 0 ][ 0 ] = grid [ 0 ][ 0 ] ; // Direction vector to move in 4 directions int [][] dir = {{ - 1 0 } { 1 0 } { 0 - 1 } { 0 1 }}; pq . offer ( new int [] { grid [ 0 ][ 0 ] 0 0 }); while ( ! pq . isEmpty ()) { int [] top = pq . poll (); int c = top [ 0 ] i = top [ 1 ] j = top [ 2 ] ; // Check for all 4 neighbouring cells. for ( int [] d : dir ) { int x = i + d [ 0 ] ; int y = j + d [ 1 ] ; // If cell is valid and cost to reach this cell // from current cell is less if ( isValidCell ( x y n ) && cost [ i ][ j ] + grid [ x ][ y ] < cost [ x ][ y ] ) { // Update cost to reach this cell. cost [ x ][ y ] = cost [ i ][ j ] + grid [ x ][ y ] ; // Push the cell into heap. pq . offer ( new int [] { cost [ x ][ y ] x y }); } } } // Return minimum cost to // reach bottom right cell. return cost [ n - 1 ][ n - 1 ] ; } public static void main ( String [] args ) { int [][] grid = { { 9 4 9 9 } { 6 7 6 4 } { 8 3 3 7 } { 7 4 9 10 } }; System . out . println ( minimumCostPath ( grid )); } }
Python # Python program to find minimum Cost Path with # Left Right Bottom and Up moves allowed import heapq # Function to check if cell is valid. def isValidCell ( i j n ): return i >= 0 and i < n and j >= 0 and j < n def minimumCostPath ( grid ): n = len ( grid ) # Min heap to implement Dijkstra pq = [] # 2D grid to store minimum cost # to reach every cell. cost = [[ float ( 'inf' )] * n for _ in range ( n )] cost [ 0 ][ 0 ] = grid [ 0 ][ 0 ] # Direction vector to move in 4 directions dir = [[ - 1 0 ] [ 1 0 ] [ 0 - 1 ] [ 0 1 ]] heapq . heappush ( pq [ grid [ 0 ][ 0 ] 0 0 ]) while pq : c i j = heapq . heappop ( pq ) # Check for all 4 neighbouring cells. for d in dir : x y = i + d [ 0 ] j + d [ 1 ] # If cell is valid and cost to reach this cell # from current cell is less if isValidCell ( x y n ) and cost [ i ][ j ] + grid [ x ][ y ] < cost [ x ][ y ]: # Update cost to reach this cell. cost [ x ][ y ] = cost [ i ][ j ] + grid [ x ][ y ] # Push the cell into heap. heapq . heappush ( pq [ cost [ x ][ y ] x y ]) # Return minimum cost to # reach bottom right cell. return cost [ n - 1 ][ n - 1 ] if __name__ == '__main__' : grid = [ [ 9 4 9 9 ] [ 6 7 6 4 ] [ 8 3 3 7 ] [ 7 4 9 10 ] ] print ( minimumCostPath ( grid ))
C# // C# program to find minimum Cost Path with // Left Right Bottom and Up moves allowed using System ; using System.Collections.Generic ; class GfG { // Function to check if cell is valid. static bool isValidCell ( int i int j int n ) { return i >= 0 && i < n && j >= 0 && j < n ; } static int minimumCostPath ( int [][] grid ) { int n = grid . Length ; // Min heap to implement Dijkstra var pq = new SortedSet < ( int cost int x int y ) > (); // 2D grid to store minimum cost // to reach every cell. int [][] cost = new int [ n ][]; for ( int i = 0 ; i < n ; i ++ ) { cost [ i ] = new int [ n ]; Array . Fill ( cost [ i ] int . MaxValue ); } cost [ 0 ][ 0 ] = grid [ 0 ][ 0 ]; // Direction vector to move in 4 directions int [][] dir = { new int [] { - 1 0 } new int [] { 1 0 } new int [] { 0 - 1 } new int [] { 0 1 } }; pq . Add (( grid [ 0 ][ 0 ] 0 0 )); while ( pq . Count > 0 ) { var top = pq . Min ; pq . Remove ( top ); int i = top . x j = top . y ; // Check for all 4 neighbouring cells. foreach ( var d in dir ) { int x = i + d [ 0 ]; int y = j + d [ 1 ]; // If cell is valid and cost to reach this cell // from current cell is less if ( isValidCell ( x y n ) && cost [ i ][ j ] + grid [ x ][ y ] < cost [ x ][ y ]) { // Update cost to reach this cell. cost [ x ][ y ] = cost [ i ][ j ] + grid [ x ][ y ]; // Push the cell into heap. pq . Add (( cost [ x ][ y ] x y )); } } } // Return minimum cost to // reach bottom right cell. return cost [ n - 1 ][ n - 1 ]; } static void Main ( string [] args ) { int [][] grid = new int [][] { new int [] { 9 4 9 9 } new int [] { 6 7 6 4 } new int [] { 8 3 3 7 } new int [] { 7 4 9 10 } }; Console . WriteLine ( minimumCostPath ( grid )); } }
JavaScript // JavaScript program to find minimum Cost Path with // Left Right Bottom and Up moves allowed function comparator ( a b ) { if ( a [ 0 ] > b [ 0 ]) return - 1 ; if ( a [ 0 ] < b [ 0 ]) return 1 ; return 0 ; } class PriorityQueue { constructor ( compare ) { this . heap = []; this . compare = compare ; } enqueue ( value ) { this . heap . push ( value ); this . bubbleUp (); } bubbleUp () { let index = this . heap . length - 1 ; while ( index > 0 ) { let element = this . heap [ index ] parentIndex = Math . floor (( index - 1 ) / 2 ) parent = this . heap [ parentIndex ]; if ( this . compare ( element parent ) < 0 ) break ; this . heap [ index ] = parent ; this . heap [ parentIndex ] = element ; index = parentIndex ; } } dequeue () { let max = this . heap [ 0 ]; let end = this . heap . pop (); if ( this . heap . length > 0 ) { this . heap [ 0 ] = end ; this . sinkDown ( 0 ); } return max ; } sinkDown ( index ) { let left = 2 * index + 1 right = 2 * index + 2 largest = index ; if ( left < this . heap . length && this . compare ( this . heap [ left ] this . heap [ largest ]) > 0 ) { largest = left ; } if ( right < this . heap . length && this . compare ( this . heap [ right ] this . heap [ largest ]) > 0 ) { largest = right ; } if ( largest !== index ) { [ this . heap [ largest ] this . heap [ index ]] = [ this . heap [ index ] this . heap [ largest ] ]; this . sinkDown ( largest ); } } isEmpty () { return this . heap . length === 0 ; } } // Function to check if cell is valid. function isValidCell ( i j n ) { return i >= 0 && i < n && j >= 0 && j < n ; } function minimumCostPath ( grid ) { let n = grid . length ; // Min heap to implement Dijkstra const pq = new PriorityQueue ( comparator ) // 2D grid to store minimum cost // to reach every cell. let cost = Array . from ({ length : n } () => Array ( n ). fill ( Infinity )); cost [ 0 ][ 0 ] = grid [ 0 ][ 0 ]; // Direction vector to move in 4 directions let dir = [[ - 1 0 ] [ 1 0 ] [ 0 - 1 ] [ 0 1 ]]; pq . enqueue ([ grid [ 0 ][ 0 ] 0 0 ]); while ( ! pq . isEmpty ()) { let [ c i j ] = pq . dequeue (); // Check for all 4 neighbouring cells. for ( let d of dir ) { let x = i + d [ 0 ]; let y = j + d [ 1 ]; // If cell is valid and cost to reach this cell // from current cell is less if ( isValidCell ( x y n ) && cost [ i ][ j ] + grid [ x ][ y ] < cost [ x ][ y ]) { // Update cost to reach this cell. cost [ x ][ y ] = cost [ i ][ j ] + grid [ x ][ y ]; // Push the cell into heap. pq . enqueue ([ cost [ x ][ y ] x y ]); } } } // Return minimum cost to // reach bottom right cell. return cost [ n - 1 ][ n - 1 ]; } let grid = [ [ 9 4 9 9 ] [ 6 7 6 4 ] [ 8 3 3 7 ] [ 7 4 9 10 ] ]; console . log ( minimumCostPath ( grid ));
Výstup
43
Časová zložitosť: O(n^2 log(n^2))
Pomocný priestor: O(n^2 log(n^2))
Prečo nie je možné použiť dynamické programovanie?
Dynamické programovanie tu zlyháva, pretože umožnenie pohybu vo všetkých štyroch smeroch vytvára cykly, v ktorých možno bunky prehodnotiť, čím sa poruší predpoklad optimálnej subštruktúry. To znamená, že cena za dosiahnutie bunky z danej bunky nie je pevná, ale závisí od celej cesty.
Súvisiace články:
Cesta minimálnych nákladov
Vytvoriť kvíz