Tento tutoriál je príručkou pre začiatočníkov učenie dátových štruktúr a algoritmov pomocou Pythonu. V tomto článku budeme diskutovať o vstavaných dátových štruktúrach, ako sú zoznamy, n-tice, slovníky atď., a niektorých užívateľom definovaných dátových štruktúrach, ako napr. prepojené zoznamy , stromy , grafov , atď, a prechádzanie, ako aj vyhľadávanie a triedenie algoritmov pomocou dobrých a dobre vysvetlených príkladov a praktických otázok.

zoznamy

Python zoznamy sú usporiadané kolekcie údajov rovnako ako polia v iných programovacích jazykoch. Umožňuje rôzne typy prvkov v zozname. Implementácia Python Listu je podobná ako Vectors v C++ alebo ArrayList v JAVA. Nákladnou operáciou je vloženie alebo odstránenie prvku zo začiatku zoznamu, pretože je potrebné presunúť všetky prvky. Vkladanie a vymazávanie na konci zoznamu môže byť tiež nákladné v prípade, že sa vopred pridelená pamäť zaplní.

Príklad: Vytvorenie zoznamu Python

List = [1, 2, 3, 'GFG', 2.3] print(List) 

[1, 2, 3, 'GFG', 2.3] 

Prvky zoznamu sú prístupné pomocou priradeného indexu. V python počiatočnom indexe zoznamu je sekvencia 0 a koncový index je (ak je tam N prvkov) N-1.

Príklad: Operácie zoznamu Python

# Creating a List with # the use of multiple values List = ['Geeks', 'For', 'Geeks'] print('
List containing multiple values: ') print(List) # Creating a Multi-Dimensional List # (By Nesting a list inside a List) List2 = [['Geeks', 'For'], ['Geeks']] print('
Multi-Dimensional List: ') print(List2) # accessing a element from the # list using index number print('Accessing element from the list') print(List[0]) print(List[2]) # accessing a element using # negative indexing print('Accessing element using negative indexing') # print the last element of list print(List[-1]) # print the third last element of list print(List[-3]) 

List containing multiple values: ['Geeks', 'For', 'Geeks'] Multi-Dimensional List: [['Geeks', 'For'], ['Geeks']] Accessing element from the list Geeks Geeks Accessing element using negative indexing Geeks Geeks 

Násobný

Python n-tice sú podobné zoznamom, ale n-tice sú nemenný v prírode, t. j. raz vytvorený nemôže byť modifikovaný. Rovnako ako zoznam, aj tuple môže obsahovať prvky rôznych typov.

V Pythone sa n-tice vytvárajú umiestnením sekvencie hodnôt oddelených „čiarkou“ s použitím alebo bez použitia zátvoriek na zoskupenie sekvencie údajov.

Poznámka: Na vytvorenie n-tice jedného prvku musí byť koncová čiarka. Napríklad (8,) vytvorí n-ticu obsahujúcu 8 ako prvok.

Príklad: Python Tuple Operations

# Creating a Tuple with # the use of Strings Tuple = ('Geeks', 'For') print('
Tuple with the use of String: ') print(Tuple) # Creating a Tuple with # the use of list list1 = [1, 2, 4, 5, 6] print('
Tuple using List: ') Tuple = tuple(list1) # Accessing element using indexing print('First element of tuple') print(Tuple[0]) # Accessing element from last # negative indexing print('
Last element of tuple') print(Tuple[-1]) print('
Third last element of tuple') print(Tuple[-3]) 

Tuple with the use of String: ('Geeks', 'For') Tuple using List: First element of tuple 1 Last element of tuple 6 Third last element of tuple 4 

Set

Sada Python je meniteľný súbor údajov, ktorý neumožňuje žiadne duplikovanie. Sady sa v podstate používajú na testovanie členstva a odstránenie duplicitných záznamov. Štruktúra údajov, ktorá sa tu používa, je hashovanie, populárna technika na vykonávanie vkladania, vymazania a prechodu v priemere v O(1).

Ak sa na rovnakej pozícii indexu nachádza viacero hodnôt, hodnota sa pripojí k tejto pozícii indexu a vytvorí sa tak prepojený zoznam. Sady CPython sú implementované pomocou slovníka s fiktívnymi premennými, kde kľúčové bytosti nastavujú členovia s väčšou optimalizáciou na časovú zložitosť.

Implementácia sady:

Sady s množstvom operácií na jednej HashTable:

Príklad: Operácie množiny Pythonu

# Creating a Set with # a mixed type of values # (Having numbers and strings) Set = set([1, 2, 'Geeks', 4, 'For', 6, 'Geeks']) print('
Set with the use of Mixed Values') print(Set) # Accessing element using # for loop print('
Elements of set: ') for i in Set: print(i, end =' ') print() # Checking the element # using in keyword print('Geeks' in Set) 

Set with the use of Mixed Values {1, 2, 4, 6, 'For', 'Geeks'} Elements of set: 1 2 4 6 For Geeks True 

Mrazené súpravy

Mrazené súpravy v Pythone sú nemenné objekty, ktoré podporujú iba metódy a operátory, ktoré vytvárajú výsledok bez ovplyvnenia zmrazenej množiny alebo množín, na ktoré sú aplikované. Zatiaľ čo prvky množiny možno kedykoľvek upraviť, prvky zamrznutej množiny zostanú po vytvorení rovnaké.

Príklad: Sada Python Frozen

# Same as {'a', 'b','c'} normal_set = set(['a', 'b','c']) print('Normal Set') print(normal_set) # A frozen set frozen_set = frozenset(['e', 'f', 'g']) print('
Frozen Set') print(frozen_set) # Uncommenting below line would cause error as # we are trying to add element to a frozen set # frozen_set.add('h') 

Normal Set {'a', 'b', 'c'} Frozen Set frozenset({'f', 'g', 'e'}) 

Reťazec

Python Strings je nemenné pole bajtov predstavujúce znaky Unicode. Python nemá dátový typ znaku, jeden znak je jednoducho reťazec s dĺžkou 1.

Poznámka: Keďže reťazce sú nemenné, úprava reťazca povedie k vytvoreniu novej kópie.

Príklad: Python Strings Operations

String = 'Welcome to GeeksForGeeks' print('Creating String: ') print(String) # Printing First character print('
First character of String is: ') print(String[0]) # Printing Last character print('
Last character of String is: ') print(String[-1]) 

Creating String: Welcome to GeeksForGeeks First character of String is: W Last character of String is: s 

Slovník

Pythonský slovník je neusporiadaná kolekcia údajov, ktorá ukladá údaje vo formáte páru kľúč:hodnota. Je to ako hašovacie tabuľky v akomkoľvek inom jazyku s časovou zložitosťou O(1). Indexovanie Python Dictionary sa vykonáva pomocou kľúčov. Sú akéhokoľvek hašovateľného typu, t. j. objekty, ktoré sa nikdy nemôžu meniť ako reťazce, čísla, n-tice atď. Slovník môžeme vytvoriť pomocou zložených zátvoriek ({}) alebo porozumením slovníka.

Príklad: Operácie slovníka Python

# Creating a Dictionary Dict = {'Name': 'Geeks', 1: [1, 2, 3, 4]} print('Creating Dictionary: ') print(Dict) # accessing a element using key print('Accessing a element using key:') print(Dict['Name']) # accessing a element using get() # method print('Accessing a element using get:') print(Dict.get(1)) # creation using Dictionary comprehension myDict = {x: x**2 for x in [1,2,3,4,5]} print(myDict) 

Creating Dictionary: {'Name': 'Geeks', 1: [1, 2, 3, 4]} Accessing a element using key: Geeks Accessing a element using get: [1, 2, 3, 4] {1: 1, 2: 4, 3: 9, 4: 16, 5: 25} 

Matrix

Matica je 2D pole, kde má každý prvok presne rovnakú veľkosť. Na vytvorenie matice použijeme Balík NumPy .

Príklad: Python NumPy Matrix Operations

import numpy as np a = np.array([[1,2,3,4],[4,55,1,2], [8,3,20,19],[11,2,22,21]]) m = np.reshape(a,(4, 4)) print(m) # Accessing element print('
Accessing Elements') print(a[1]) print(a[2][0]) # Adding Element m = np.append(m,[[1, 15,13,11]],0) print('
Adding Element') print(m) # Deleting Element m = np.delete(m,[1],0) print('
Deleting Element') print(m) 

Výkon

[[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]] Accessing Elements [ 4 55 1 2] 8 Adding Element [[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]] Deleting Element [[ 1 2 3 4]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]] 

Bytearray

Python Bytearray poskytuje meniteľnú sekvenciu celých čísel v rozsahu 0 <= x < 256.

Príklad: Operácie Python Bytearray

# Creating bytearray a = bytearray((12, 8, 25, 2)) print('Creating Bytearray:') print(a) # accessing elements print('
Accessing Elements:', a[1]) # modifying elements a[1] = 3 print('
After Modifying:') print(a) # Appending elements a.append(30) print('
After Adding Elements:') print(a) 

Creating Bytearray: bytearray(b'x0cx08x19x02') Accessing Elements: 8 After Modifying: bytearray(b'x0cx03x19x02') After Adding Elements: bytearray(b'x0cx03x19x02x1e') 

Prepojený zoznam

A prepojený zoznam je lineárna dátová štruktúra, v ktorej prvky nie sú uložené na súvislých pamäťových miestach. Prvky v prepojenom zozname sú prepojené pomocou ukazovateľov, ako je znázornené na obrázku nižšie:

Prepojený zoznam je reprezentovaný ukazovateľom na prvý uzol prepojeného zoznamu. Prvý uzol sa nazýva hlava. Ak je prepojený zoznam prázdny, hodnota hlavičky je NULL. Každý uzol v zozname pozostáva najmenej z dvoch častí:

• Údaje
• Ukazovateľ (alebo odkaz) na nasledujúci uzol

Príklad: Definovanie prepojeného zoznamu v Pythone

# Node class class Node: # Function to initialize the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize # next as null # Linked List class class LinkedList: # Function to initialize the Linked # List object def __init__(self): self.head = None 

Vytvorme jednoduchý prepojený zoznam s 3 uzlami.

# A simple Python program to introduce a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3)  '''  Three nodes have been created.  We have references to these three blocks as head,  second and third  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | None | | 2 | None | | 3 | None |  +----+------+ +----+------+ +----+------+  ''' llist.head.next = second; # Link first node with second  '''  Now next of first Node refers to second. So they  both are linked.  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | o-------->| 2 | null | | 3 | null |  +----+------+ +----+------+ +----+------+ ''' druhý.ďalší = tretí ; # Prepojiť druhý uzol s tretím uzlom ''' Teraz ďalší z druhého uzla odkazuje na tretí. Všetky tri uzly sú teda prepojené.  llist.hlava druhá tretina | | |  | | |  +----+------+ +----+------+ +----+------+ | 1 | o-------->| 2 | o-------->| 3 | null |  +----+------+ +----+------+ +----+------+ ''' 

Prechádzanie prepojeného zoznamu

V predchádzajúcom programe sme vytvorili jednoduchý prepojený zoznam s tromi uzlami. Prejdeme vytvorený zoznam a vytlačíme údaje každého uzla. Na prechod napíšme univerzálnu funkciu printList(), ktorá vypíše ľubovoľný daný zoznam.

# A simple Python program for traversal of a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # This function prints contents of linked list # starting from head def printList(self): temp = self.head while (temp): print (temp.data) temp = temp.next # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3) llist.head.next = second; # Link first node with second second.next = third; # Link second node with the third node llist.printList() 

1 2 3 

Ďalšie články na Linked List

• Vloženie prepojeného zoznamu
• Odstránenie prepojeného zoznamu (odstránenie daného kľúča)
• Odstránenie prepojeného zoznamu (odstránenie kľúča na danej pozícii)
• Nájsť dĺžku prepojeného zoznamu (iteratívny a rekurzívny)
• Vyhľadajte prvok v prepojenom zozname (iteratívny a rekurzívny)
• N-tý uzol z konca prepojeného zoznamu
• Obrátiť prepojený zoznam

A stoh je lineárna dátová štruktúra, ktorá ukladá položky spôsobom Last-In/First-Out (LIFO) alebo First-In/Last-Out (FILO). V zásobníku sa nový prvok pridá na jeden koniec a prvok sa odstráni iba z tohto konca. Operácie vloženia a vymazania sa často nazývajú push a pop.

stack = [] # append() function to push # element in the stack stack.append('g') stack.append('f') stack.append('g') print('Initial stack') print(stack) # pop() function to pop # element from stack in # LIFO order print('
Elements popped from stack:') print(stack.pop()) print(stack.pop()) print(stack.pop()) print('
Stack after elements are popped:') print(stack) # uncommenting print(stack.pop()) # will cause an IndexError # as the stack is now empty 

Initial stack ['g', 'f', 'g'] Elements popped from stack: g f g Stack after elements are popped: [] 

Ako zásobník, frontu je lineárna dátová štruktúra, ktorá ukladá položky spôsobom First In First Out (FIFO). Pri fronte sa najskôr odstráni najmenej nedávno pridaná položka. Dobrým príkladom frontu je akýkoľvek rad spotrebiteľov pre zdroj, kde je prvý obsluhovaný spotrebiteľ, ktorý prišiel ako prvý.

# Initializing a queue queue = [] # Adding elements to the queue queue.append('g') queue.append('f') queue.append('g') print('Initial queue') print(queue) # Removing elements from the queue print('
Elements dequeued from queue') print(queue.pop(0)) print(queue.pop(0)) print(queue.pop(0)) print('
Queue after removing elements') print(queue) # Uncommenting print(queue.pop(0)) # will raise and IndexError # as the queue is now empty 

Initial queue ['g', 'f', 'g'] Elements dequeued from queue g f g Queue after removing elements [] 

Prioritné fronty sú abstraktné dátové štruktúry, kde každý údaj/hodnota vo fronte má určitú prioritu. Napríklad v leteckých spoločnostiach prichádza batožina s názvom Business alebo First-class skôr ako ostatné. Prioritný front je rozšírenie frontu s nasledujúcimi vlastnosťami.

• Prvok s vysokou prioritou je vyradený pred prvok s nízkou prioritou.
• Ak majú dva prvky rovnakú prioritu, obslúžia sa podľa poradia vo fronte.

# A simple implementation of Priority Queue # using Queue. class PriorityQueue(object): def __init__(self): self.queue = [] def __str__(self): return ' '.join([str(i) for i in self.queue]) # for checking if the queue is empty def isEmpty(self): return len(self.queue) == 0 # for inserting an element in the queue def insert(self, data): self.queue.append(data) # for popping an element based on Priority def delete(self): try: max = 0 for i in range(len(self.queue)): if self.queue[i]>self.queue[max]: max = i item = self.queue[max] del self.queue[max] return item okrem IndexError: print() exit() if __name__ == '__main__': myQueue = PriorityQueue( ) myQueue.insert(12) myQueue.insert(1) myQueue.insert(14) myQueue.insert(7) print(myQueue) pričom nie myQueue.isEmpty(): print(myQueue.delete()) 

12 1 14 7 14 12 7 1 

Hromada

modul heapq v Pythone poskytuje štruktúru údajov haldy, ktorá sa používa hlavne na reprezentáciu prioritného frontu. Vlastnosťou tejto dátovej štruktúry je, že vždy dáva najmenší prvok (min haldu) vždy, keď sa prvok objaví. Vždy, keď sú prvky zatlačené alebo vyskočené, štruktúra haldy sa zachová. Prvok haldy[0] tiež zakaždým vráti najmenší prvok. Podporuje extrakciu a vloženie najmenšieho prvku v O(log n) časoch.

Vo všeobecnosti môžu byť haldy dvoch typov:

• Max-Heap: V Max-Heap kľúč prítomný v koreňovom uzle musí byť najväčší spomedzi kľúčov prítomných u všetkých jeho potomkov. Rovnaká vlastnosť musí byť rekurzívne pravdivá pre všetky podstromy v tomto binárnom strome.
• Minimálna halda: V Min-Heap kľúč prítomný v koreňovom uzle musí byť minimálny medzi kľúčmi prítomnými u všetkých jeho potomkov. Rovnaká vlastnosť musí byť rekurzívne pravdivá pre všetky podstromy v tomto binárnom strome.

# importing 'heapq' to implement heap queue import heapq # initializing list li = [5, 7, 9, 1, 3] # using heapify to convert list into heap heapq.heapify(li) # printing created heap print ('The created heap is : ',end='') print (list(li)) # using heappush() to push elements into heap # pushes 4 heapq.heappush(li,4) # printing modified heap print ('The modified heap after push is : ',end='') print (list(li)) # using heappop() to pop smallest element print ('The popped and smallest element is : ',end='') print (heapq.heappop(li)) 

The created heap is : [1, 3, 9, 7, 5] The modified heap after push is : [1, 3, 4, 7, 5, 9] The popped and smallest element is : 1 

Ďalšie články o halde

• Binárna halda
• K’th Najväčší prvok v poli
• K’th najmenší/najväčší prvok v netriedenom poli
• Zoradiť takmer zoradené pole
• K-té súvislé podpolie s najväčšou sumou
• Minimálny súčet dvoch čísel vytvorených z číslic poľa

Strom je hierarchická dátová štruktúra, ktorá vyzerá ako na obrázku nižšie –

 tree  ----  j  <-- root  /   f k  /   a h z  <-- leaves 

Najvyšší uzol stromu sa nazýva koreň, zatiaľ čo najspodnejšie uzly alebo uzly bez potomkov sa nazývajú listové uzly. Uzly, ktoré sú priamo pod uzlom, sa nazývajú jeho potomkovia a uzly, ktoré sú priamo nad niečím, sa nazývajú jeho rodičia.

A binárny strom je strom, ktorého prvky môžu mať takmer dve deti. Keďže každý prvok v binárnom strome môže mať iba 2 potomkov, zvyčajne ich pomenujeme ľavé a pravé potomstvo. Uzol binárneho stromu obsahuje nasledujúce časti.

• Údaje
• Ukazovateľ na ľavé dieťa
• Ukazovateľ na správne dieťa

Príklad: Definovanie triedy uzla

# A Python class that represents an individual node # in a Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key 

Teraz vytvorte strom so 4 uzlami v Pythone. Predpokladajme, že stromová štruktúra vyzerá nižšie –

 tree  ----  1  <-- root  /   2 3   /  4 

Príklad: Pridávanie údajov do stromu

# Python program to introduce Binary Tree # A class that represents an individual node in a # Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key # create root root = Node(1) ''' following is the tree after above statement  1  /   None None''' root.left = Node(2); root.right = Node(3); ''' 2 and 3 become left and right children of 1  1  /   2 3  /  /  None None None None''' root.left.left = Node(4); '''4 becomes left child of 2  1  /   2 3  /  /  4 None None None /  None None''' 

Prechádzanie stromom

Stromy sa dajú prechádzať rôznymi spôsobmi. Nasledujú všeobecne používané spôsoby prechodu cez stromy. Pozrime sa na nižšie uvedený strom -

 tree  ----  1  <-- root  /   2 3   /  4 5 

Hĺbkové prvé prechody:

• V poradí (vľavo, koreň, vpravo): 4 2 5 1 3
• Predobjednávka (koreň, vľavo, vpravo): 1 2 4 5 3
• Postorder (vľavo, vpravo, koreň) : 4 5 2 3 1

Algoritmus Inorder (strom)

• Prejdite ľavým podstromom, t.j. zavolajte Inorder (ľavý podstrom)
• Navštívte koreň.
• Prejdite pravým podstromom, t.j. zavolajte Inorder (pravý podstrom)

Predobjednávka algoritmu (strom)

• Navštívte koreň.
• Prejdite ľavým podstromom, t. j. zavolajte Predobjednávku (ľavý podstrom)
• Prejdite pravým podstromom, t.j. zavolajte Predobjednávku (pravý podstrom)

Algoritmus Poštová poukážka (strom)

• Prejdite ľavým podstromom, t.j. zavolajte Postorder (ľavý podstrom)
• Prejdite pravým podstromom, t.j. zavolajte Postorder (pravý podstrom)
• Navštívte koreň.

# Python program to for tree traversals # A class that represents an individual node in a # Binary Tree class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A function to do inorder tree traversal def printInorder(root): if root: # First recur on left child printInorder(root.left) # then print the data of node print(root.val), # now recur on right child printInorder(root.right) # A function to do postorder tree traversal def printPostorder(root): if root: # First recur on left child printPostorder(root.left) # the recur on right child printPostorder(root.right) # now print the data of node print(root.val), # A function to do preorder tree traversal def printPreorder(root): if root: # First print the data of node print(root.val), # Then recur on left child printPreorder(root.left) # Finally recur on right child printPreorder(root.right) # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print('Preorder traversal of binary tree is') printPreorder(root) print('
Inorder traversal of binary tree is') printInorder(root) print('
Postorder traversal of binary tree is') printPostorder(root) 

Preorder traversal of binary tree is 1 2 4 5 3 Inorder traversal of binary tree is 4 2 5 1 3 Postorder traversal of binary tree is 4 5 2 3 1 

Časová zložitosť – O(n)

Priebeh poradia po šírke alebo úrovni

Priebeh objednávky úrovne stromu je prechod stromu na šírku. Prechod na úrovni vyššie uvedeného stromu je 1 2 3 4 5.

Pre každý uzol sa najprv navštívi uzol a potom sa jeho dcérske uzly zaradia do frontu FIFO. Nižšie je uvedený algoritmus pre to isté -

• Vytvorte prázdny rad q
• temp_node = root /*začať od root*/
• Slučka, zatiaľ čo temp_node nie je NULL
  • vytlačiť temp_node->data.
  • Zaraďte deti temp_node (prvé ľavé, potom pravé deti) do q
  • Vyraďte uzol z q

# Python program to print level # order traversal using Queue # A node structure class Node: # A utility function to create a new node def __init__(self ,key): self.data = key self.left = None self.right = None # Iterative Method to print the # height of a binary tree def printLevelOrder(root): # Base Case if root is None: return # Create an empty queue # for level order traversal queue = [] # Enqueue Root and initialize height queue.append(root) while(len(queue)>0): # Vytlačiť prednú časť frontu a # odstrániť ju z frontu vytlačiť (front[0].data) node = queue.pop(0) # Zaradiť ľavý potomok, ak node.left nie je Žiadne: queue.append(node.left ) # Zaradiť pravé dieťa do frontu, ak node.right nie je Žiadne: queue.append(node.right) # Program ovládača na otestovanie funkcie root = Uzol(1) root.left = Uzol(2) root.right = Uzol(3) root.left.left = Node(4) root.left.right = Node(5) print ('Prechod poradia úrovní binárneho stromu je -') printLevelOrder(root) 

Level Order Traversal of binary tree is - 1 2 3 4 5 

Časová zložitosť: O(n)

Ďalšie články na tému Binárny strom

• Vloženie do binárneho stromu
• Vymazanie v binárnom strome
• Inorder Tree Traversal bez rekurzie
• Inorder Tree Traversal bez rekurzie a bez zásobníka!
• Vytlačiť prechod Postorder z daného prechodu Inorder a Preorder
• Nájsť postorder traversal BST z preorder traversal

Binárny vyhľadávací strom je dátová štruktúra binárneho stromu založená na uzloch, ktorá má nasledujúce vlastnosti:

# A utility function to search a given key in BST def search(root,key): # Base Cases: root is null or key is present at root if root is None or root.val == key: return root # Key is greater than root's key if root.val  < key: return search(root.right,key) # Key is smaller than root's key return search(root.left,key) 

# Python program to demonstrate # insert operation in binary search tree # A utility class that represents # an individual node in a BST class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A utility function to insert # a new node with the given key def insert(root, key): if root is None: return Node(key) else: if root.val == key: return root elif root.val  < key: root.right = insert(root.right, key) else: root.left = insert(root.left, key) return root # A utility function to do inorder tree traversal def inorder(root): if root: inorder(root.left) print(root.val) inorder(root.right) # Driver program to test the above functions # Let us create the following BST # 50 # /  # 30 70 # /  /  # 20 40 60 80 r = Node(50) r = insert(r, 30) r = insert(r, 20) r = insert(r, 40) r = insert(r, 70) r = insert(r, 60) r = insert(r, 80) # Print inorder traversal of the BST inorder(r) 

20 30 40 50 60 70 80 

A graf je nelineárna dátová štruktúra pozostávajúca z uzlov a hrán. Uzly sa niekedy označujú aj ako vrcholy a hrany sú čiary alebo oblúky, ktoré spájajú ľubovoľné dva uzly v grafe. Formálnejšie možno graf definovať ako graf pozostávajúci z konečnej množiny vrcholov (alebo uzlov) a množiny hrán, ktoré spájajú pár uzlov.

# A simple representation of graph using Adjacency Matrix class Graph: def __init__(self,numvertex): self.adjMatrix = [[-1]*numvertex for x in range(numvertex)] self.numvertex = numvertex self.vertices = {} self.verticeslist =[0]*numvertex def set_vertex(self,vtx,id): if 0 <=vtx <=self.numvertex: self.vertices[id] = vtx self.verticeslist[vtx] = id def set_edge(self,frm,to,cost=0): frm = self.vertices[frm] to = self.vertices[to] self.adjMatrix[frm][to] = cost # for directed graph do not add this self.adjMatrix[to][frm] = cost def get_vertex(self): return self.verticeslist def get_edges(self): edges=[] for i in range (self.numvertex): for j in range (self.numvertex): if (self.adjMatrix[i][j]!=-1): edges.append((self.verticeslist[i],self.verticeslist[j],self.adjMatrix[i][j])) return edges def get_matrix(self): return self.adjMatrix G =Graph(6) G.set_vertex(0,'a') G.set_vertex(1,'b') G.set_vertex(2,'c') G.set_vertex(3,'d') G.set_vertex(4,'e') G.set_vertex(5,'f') G.set_edge('a','e',10) G.set_edge('a','c',20) G.set_edge('c','b',30) G.set_edge('b','e',40) G.set_edge('e','d',50) G.set_edge('f','e',60) print('Vertices of Graph') print(G.get_vertex()) print('Edges of Graph') print(G.get_edges()) print('Adjacency Matrix of Graph') print(G.get_matrix()) 

# A class to represent the adjacency list of the node class AdjNode: def __init__(self, data): self.vertex = data self.next = None # A class to represent a graph. A graph # is the list of the adjacency lists. # Size of the array will be the no. of the # vertices 'V' class Graph: def __init__(self, vertices): self.V = vertices self.graph = [None] * self.V # Function to add an edge in an undirected graph def add_edge(self, src, dest): # Adding the node to the source node node = AdjNode(dest) node.next = self.graph[src] self.graph[src] = node # Adding the source node to the destination as # it is the undirected graph node = AdjNode(src) node.next = self.graph[dest] self.graph[dest] = node # Function to print the graph def print_graph(self): for i in range(self.V): print('Adjacency list of vertex {}
 head'.format(i), end='') temp = self.graph[i] while temp: print(' ->{}'.format(temp.vertex), end='') temp = temp.next print(' 
') # Program ovládača pre vyššie uvedenú triedu grafu, ak __name__ == '__main__' : V = 5 graf = Graph(V) graph.add_edge(0, 1) graph.add_edge(0, 4) graph.add_edge(1, 2) graph.add_edge(1, 3) graph.add_edge(1, 4) graph.add_edge(2, 3) graph.add_edge(3, 4) graph.print_graph() 

Adjacency list of vertex 0 head ->4 -> 1 Zoznam susedstva hlavy vrcholu 1 -> 4 -> 3 -> 2 -> 0 Zoznam susedstva hlavy vrcholu 2 -> 3 -> 1 Zoznam susedstva hlavy vrcholu 3 -> 4 -> 2 -> 1 Priľahlosť zoznam vertex 4 head -> 3 -> 1 -> 0 

Prechod do šírky pretože graf je podobný prechodu stromu do šírky. Jediným háčikom je, že na rozdiel od stromov môžu grafy obsahovať cykly, takže sa môžeme opäť dostať do toho istého uzla. Aby sme sa vyhli spracovaniu uzla viac ako raz, používame boolovské navštívené pole. Pre jednoduchosť sa predpokladá, že všetky vrcholy sú dosiahnuteľné z počiatočného vrcholu.

Napríklad v nasledujúcom grafe začneme prechádzať od vrcholu 2. Keď prídeme k vrcholu 0, hľadáme všetky jeho susedné vrcholy. 2 je tiež susedný vrchol 0. Ak neoznačíme navštívené vrcholy, potom sa 2 znova spracuje a stane sa neukončujúcim procesom. Prechod do šírky nasledujúceho grafu je 2, 0, 3, 1.

# Python3 Program to print BFS traversal # from a given source vertex. BFS(int s) # traverses vertices reachable from s. from collections import defaultdict # This class represents a directed graph # using adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self,u,v): self.graph[u].append(v) # Function to print a BFS of graph def BFS(self, s): # Mark all the vertices as not visited visited = [False] * (max(self.graph) + 1) # Create a queue for BFS queue = [] # Mark the source node as # visited and enqueue it queue.append(s) visited[s] = True while queue: # Dequeue a vertex from # queue and print it s = queue.pop(0) print (s, end = ' ') # Get all adjacent vertices of the # dequeued vertex s. If a adjacent # has not been visited, then mark it # visited and enqueue it for i in self.graph[s]: if visited[i] == False: queue.append(i) visited[i] = True # Driver code # Create a graph given in # the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print ('Following is Breadth First Traversal' ' (starting from vertex 2)') g.BFS(2) 

Following is Breadth First Traversal (starting from vertex 2) 2 0 3 1 

Časová zložitosť: O(V+E) kde V je počet vrcholov v grafe a E je počet hrán v grafe.

Hĺbkové prvé vyhľadávanie alebo DFS

Prvý prechod do hĺbky pretože graf je podobný ako hĺbka prvého prechodu stromu. Jediným háčikom je, že na rozdiel od stromov môžu grafy obsahovať cykly, uzol možno navštíviť dvakrát. Ak sa chcete vyhnúť spracovaniu uzla viac ako raz, použite boolovské navštívené pole.

Algoritmus:

• Vytvorte rekurzívnu funkciu, ktorá vezme index uzla a navštívené pole.
• Označte aktuálny uzol ako navštívený a vytlačte ho.
• Prejdite všetky susedné a neoznačené uzly a zavolajte rekurzívnu funkciu s indexom susedného uzla.

# Python3 program to print DFS traversal # from a given graph from collections import defaultdict # This class represents a directed graph using # adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self, u, v): self.graph[u].append(v) # A function used by DFS def DFSUtil(self, v, visited): # Mark the current node as visited # and print it visited.add(v) print(v, end=' ') # Recur for all the vertices # adjacent to this vertex for neighbour in self.graph[v]: if neighbour not in visited: self.DFSUtil(neighbour, visited) # The function to do DFS traversal. It uses # recursive DFSUtil() def DFS(self, v): # Create a set to store visited vertices visited = set() # Call the recursive helper function # to print DFS traversal self.DFSUtil(v, visited) # Driver code # Create a graph given # in the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print('Following is DFS from (starting from vertex 2)') g.DFS(2) 

Following is DFS from (starting from vertex 2) 2 0 1 3 

Ďalšie články o grafe

• Reprezentácie grafov pomocou množiny a hash
• Nájdite materský vertex v grafe
• Iteratívne hĺbkové prvé vyhľadávanie
• Spočítajte počet uzlov na danej úrovni v strome pomocou BFS
• Spočítajte všetky možné cesty medzi dvoma vrcholmi

Proces, v ktorom sa funkcia volá priamo alebo nepriamo, sa nazýva rekurzia a zodpovedajúca funkcia sa nazýva a rekurzívna funkcia . Pomocou rekurzívnych algoritmov je možné niektoré problémy vyriešiť pomerne jednoducho. Príklady takýchto problémov sú Towers of Hanoi (TOH), Inorder/Preorder/Postorder Tree Traversals, DFS of Graph atď.

def fact(n):  # base case  if (n  <= 1)   return 1  else   return n*fact(n-1) 

# A Python 3 program to # demonstrate working of # recursion def printFun(test): if (test  < 1): return else: print(test, end=' ') printFun(test-1) # statement 2 print(test, end=' ') return # Driver Code test = 3 printFun(test) 

3 2 1 1 2 3 

• Rekurzia
• Rekurzia v Pythone
• Cvičné otázky pre rekurziu | Set 1
• Cvičné otázky pre rekurziu | Súprava 2
• Cvičné otázky pre rekurziu | Súprava 3
• Cvičné otázky pre rekurziu | Súprava 4
• Cvičné otázky pre rekurziu | Set 5
• Cvičné otázky pre rekurziu | Súprava 6
• Cvičné otázky pre rekurziu | Súprava 7

>>> Viac

Dynamické programovanie

Dynamické programovanie je hlavne optimalizácia oproti obyčajnej rekurzii. Kdekoľvek vidíme rekurzívne riešenie, ktoré má opakované volania pre rovnaké vstupy, môžeme ho optimalizovať pomocou dynamického programovania. Myšlienkou je jednoducho uložiť výsledky čiastkových problémov, aby sme ich v prípade potreby neskôr nemuseli znova prepočítavať. Táto jednoduchá optimalizácia znižuje časovú zložitosť z exponenciálneho na polynóm. Napríklad, ak napíšeme jednoduché rekurzívne riešenie pre Fibonacciho čísla, dostaneme exponenciálnu časovú zložitosť a ak ju optimalizujeme ukladaním riešení podproblémov, časová zložitosť sa zníži na lineárnu.

Tabuľka verzus memoizácia

Existujú dva rôzne spôsoby uloženia hodnôt, aby bolo možné znova použiť hodnoty čiastkového problému. Tu budeme diskutovať o dvoch vzorcoch riešenia problému dynamického programovania (DP):

• Tabuľka: Zdola nahor
• Zapamätanie: Hore nadol

Tabuľkovanie

Ako už samotný názov napovedá, začať zdola a zhromažďovať odpovede nahor. Poďme diskutovať o prechode štátu.

Popíšme stav nášho problému DP ako dp[x] s dp[0] ako základný stav a dp[n] ako náš cieľový stav. Potrebujeme teda nájsť hodnotu cieľového stavu, tj dp[n].

Ak začneme náš prechod z nášho základného stavu, t. spodný základný stav a dosiahol najvyšší požadovaný stav.

Prečo to teraz nazývame tabuľkovou metódou?

Aby sme to vedeli, napíšme najprv nejaký kód na výpočet faktoriálu čísla pomocou prístupu zdola nahor. Opäť ako náš všeobecný postup na riešenie DP najprv definujeme stav. V tomto prípade definujeme stav ako dp[x], kde dp[x] je nájsť faktoriál x.

Teraz je celkom zrejmé, že dp[x+1] = dp[x] * (x+1)

# Tabulated version to find factorial x. dp = [0]*MAXN # base case dp[0] = 1; for i in range(n+1):  dp[i] = dp[i-1] * i 

Zapamätanie

Ešte raz to popíšme z hľadiska prechodu stavu. Ak potrebujeme nájsť hodnotu pre nejaký stav, povedzme dp[n] a namiesto toho, aby sme začali od základného stavu, t.j. dp[0], pýtame sa na odpoveď od štátov, ktoré môžu po prechode stavu dosiahnuť cieľový stav dp[n] vzťah, potom je to spôsob DP zhora nadol.

Tu začneme našu cestu od najvyššieho cieľového stavu a vypočítame jej odpoveď počítaním hodnôt stavov, ktoré môžu dosiahnuť cieľový stav, až kým nedosiahneme najnižší základný stav.

Ešte raz, napíšme kód faktoriálneho problému spôsobom zhora nadol

# Memoized version to find factorial x. # To speed up we store the values # of calculated states # initialized to -1 dp[0]*MAXN # return fact x! def solve(x):  if (x==0)  return 1  if (dp[x]!=-1)  return dp[x]  return (dp[x] = x * solve(x-1)) 

Ďalšie články o dynamickom programovaní

• Optimálna vlastnosť spodnej stavby
• Vlastnosť prekrývajúcich sa podproblémov
• Fibonacciho čísla
• Podmnožina so súčtom deliteľným m
• Následná postupnosť zvyšovania maximálnej sumy
• Najdlhší spoločný podreťazec

>>> Viac

Algoritmy vyhľadávania

Lineárne vyhľadávanie

• Začnite od ľavého prvku arr[] a jeden po druhom porovnajte x s každým prvkom arr[]
• Ak sa x zhoduje s prvkom, vráťte index.
• Ak sa x nezhoduje so žiadnym z prvkov, vráťte -1.

# Python3 code to linearly search x in arr[]. # If x is present then return its location, # otherwise return -1 def search(arr, n, x): for i in range(0, n): if (arr[i] == x): return i return -1 # Driver Code arr = [2, 3, 4, 10, 40] x = 10 n = len(arr) # Function call result = search(arr, n, x) if(result == -1): print('Element is not present in array') else: print('Element is present at index', result) 

Element is present at index 3 

Časová zložitosť vyššie uvedeného algoritmu je O(n).

Ďalšie informácie nájdete v časti Lineárne vyhľadávanie .

Binárne vyhľadávanie

Vyhľadajte zoradené pole opakovaným delením intervalu vyhľadávania na polovicu. Začnite s intervalom pokrývajúcim celé pole. Ak je hodnota kľúča vyhľadávania menšia ako položka v strede intervalu, zúžte interval na dolnú polovicu. V opačnom prípade ju zúžte na hornú polovicu. Opakovane kontrolujte, kým nenájdete hodnotu alebo kým nebude interval prázdny.

# Python3 Program for recursive binary search. # Returns index of x in arr if present, else -1 def binarySearch (arr, l, r, x): # Check base case if r>= l: mid = l + (r - l) // 2 # Ak je prvok prítomný v samotnom strede if arr[mid] == x: return mid # Ak je prvok menší ako stred, potom # môže byť prítomný iba v ľavom podpole elif arr[mid]> x: return binarySearch(arr, l, mid-1, x) # Inak prvok môže byť prítomný iba # v pravom podpole else: return binarySearch(arr, mid + 1, r, x ) else: # Prvok nie je prítomný v poli return -1 # Kód ovládača arr = [ 2, 3, 4, 10, 40 ] x = 10 # Výsledok volania funkcie = binarySearch(arr, 0, len(arr)-1 , x) if result != -1: print ('Element je prítomný na indexe % d' % result) else: print ('Element nie je prítomný v poli') 

Element is present at index 3 

Časová zložitosť vyššie uvedeného algoritmu je O(log(n)).

Ďalšie informácie nájdete v časti Binárne vyhľadávanie .

Algoritmy triedenia

Výber Zoradiť

The triedenie výberu Algoritmus triedi pole opakovaným nájdením minimálneho prvku (vzhľadom na vzostupné poradie) z nezoradenej časti a jeho umiestnením na začiatok. V každej iterácii triedenia výberu sa vyberie minimálny prvok (vzhľadom na vzostupné poradie) z nezoradeného podpola a presunie sa do zoradeného podpola.

Vývojový diagram triedenia výberu:

# Python program for implementation of Selection # Sort import sys A = [64, 25, 12, 22, 11] # Traverse through all array elements for i in range(len(A)): # Find the minimum element in remaining # unsorted array min_idx = i for j in range(i+1, len(A)): if A[min_idx]>A[j]: min_idx = j # Vymeňte nájdený minimálny prvok za # prvý prvok A[i], A[min_idx] = A[min_idx], A[i] # Kód ovládača na testovanie vyššie ('Sorted array ') pre i v rozsahu (len(A)): print('%d' %A[i]), 

Sorted array 11 12 22 25 64 

Časová zložitosť: O(n ² ), pretože existujú dve vnorené slučky.

Pomocný priestor: O(1)

Bublinové triedenie

Bublinové triedenie je najjednoduchší triediaci algoritmus, ktorý funguje tak, že opakovane zamieňa susedné prvky, ak sú v nesprávnom poradí.

Ilustrácia:

# Python program for implementation of Bubble Sort def bubbleSort(arr): n = len(arr) # Traverse through all array elements for i in range(n): # Last i elements are already in place for j in range(0, n-i-1): # traverse the array from 0 to n-i-1 # Swap if the element found is greater # than the next element if arr[j]>arr[j+1] : arr[j], arr[j+1] = arr[j+1], arr[j] # Kód ovládača na testovanie vyššie arr = [64, 34, 25, 12, 22, 11 , 90] bubbleSort(arr) print ('Sorted array is:') for i in range(len(arr)): print ('%d' %arr[i]), 

Sorted array is: 11 12 22 25 34 64 90 

Časová zložitosť: O(n ² )

Triedenie vloženia

Ak chcete zoradiť pole veľkosti n vo vzostupnom poradí pomocou triedenie vloženia :

• Iterujte z arr[1] do arr[n] cez pole.
• Porovnajte aktuálny prvok (kľúč) s jeho predchodcom.
• Ak je kľúčový prvok menší ako jeho predchodca, porovnajte ho s predchádzajúcimi prvkami. Posuňte väčšie prvky o jednu pozíciu nahor, aby ste vytvorili priestor pre vymenený prvok.

Ilustrácia:

# Python program for implementation of Insertion Sort # Function to do insertion sort def insertionSort(arr): # Traverse through 1 to len(arr) for i in range(1, len(arr)): key = arr[i] # Move elements of arr[0..i-1], that are # greater than key, to one position ahead # of their current position j = i-1 while j>= 0 a kľúč < arr[j] : arr[j + 1] = arr[j] j -= 1 arr[j + 1] = key # Driver code to test above arr = [12, 11, 13, 5, 6] insertionSort(arr) for i in range(len(arr)): print ('% d' % arr[i]) 

 5 6 11 12 13 

Časová zložitosť: O(n ² ))

Zlúčiť triedenie

Rovnako ako QuickSort, Zlúčiť triedenie je algoritmus rozdeľuj a panuj. Rozdelí vstupné pole na dve polovice, zavolá sa pre dve polovice a potom zlúči dve zoradené polovice. Funkcia merge() sa používa na spojenie dvoch polovíc. Zlúčenie (arr, l, m, r) je kľúčový proces, ktorý predpokladá, že arr[l..m] a arr[m+1..r] sú zoradené a zlučuje dve zoradené podpolia do jedného.

MergeSort(arr[], l, r) If r>l 1. Nájdite stredný bod na rozdelenie poľa na dve polovice: stredná m = l+ (r-l)/2 2. Zavolajte mergeSort pre prvú polovicu: Zavolajte mergeSort(arr, l, m) 3. Zavolajte mergeSort pre druhú polovicu: Zavolajte mergeSort(arr, m+1, r) 4. Zlúčte dve polovice zoradené v kroku 2 a 3: Zavolajte zlúčenie(arr, l, m, r) 

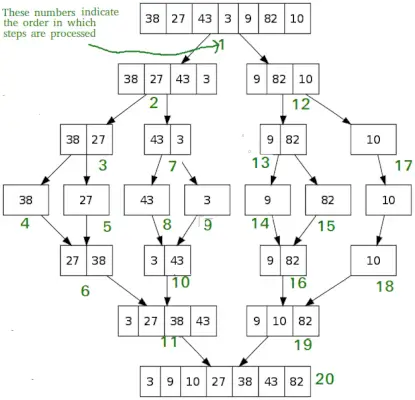
# Python program for implementation of MergeSort def mergeSort(arr): if len(arr)>1: # Nájdenie stredu poľa mid = len(arr)//2 # Rozdelenie prvkov poľa L = arr[:mid] # na 2 polovice R = arr[mid:] # Triedenie prvej polovice mergeSort(L) # Triedenie druhej polovice mergeSort(R) i = j = k = 0 # Kopírovanie údajov do temp polí L[] a R[], zatiaľ čo i < len(L) and j  < len(R): if L[i]  < R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 # Checking if any element was left while i  < len(L): arr[k] = L[i] i += 1 k += 1 while j  < len(R): arr[k] = R[j] j += 1 k += 1 # Code to print the list def printList(arr): for i in range(len(arr)): print(arr[i], end=' ') print() # Driver Code if __name__ == '__main__': arr = [12, 11, 13, 5, 6, 7] print('Given array is', end='
') printList(arr) mergeSort(arr) print('Sorted array is: ', end='
') printList(arr) 

Given array is 12 11 13 5 6 7 Sorted array is: 5 6 7 11 12 13 

Časová zložitosť: O(n(logn))

QuickSort

Ako Merge Sort, QuickSort je algoritmus rozdeľuj a panuj. Vyberie prvok ako pivot a rozdelí dané pole okolo vybratého pivotu. Existuje mnoho rôznych verzií quickSort, ktoré vyberajú pivot rôznymi spôsobmi.

Vždy vyberte prvý prvok ako pivot.

• Vždy vybrať posledný prvok ako pivot (implementované nižšie)
• Vyberte náhodný prvok ako pivot.
• Vyberte medián ako pivot.

Kľúčovým procesom v quickSort je partition(). Cieľ oddielov je, ak je dané pole a prvok x poľa ako pivot, umiestniť x na správnu pozíciu v triedenom poli a všetky menšie prvky (menšie ako x) umiestniť pred x a všetky väčšie prvky (väčšie ako x) umiestniť za X. To všetko by sa malo uskutočniť v lineárnom čase.

/* low -->Počiatočný index, vysoký --> Konečný index */ quickSort(arr[], low, high) { if (low { /* pi je index rozdelenia, arr[pi] je teraz na správnom mieste */ pi = partition(arr, low, high; quickSort(arr, low, pi - 1); // Pred pi quickSort(arr, pi + 1, high);  
  
  
    Algoritmus rozdelenia     
  
 Existuje mnoho spôsobov, ako urobiť rozdelenie, nasledujúce    pseudo kód    používa metódu uvedenú v knihe CLRS. Logika je jednoduchá, začíname od prvku úplne vľavo a sledujeme index menších (alebo rovných) prvkov ako i. Ak pri prechádzaní nájdeme menší prvok, vymeníme aktuálny prvok za arr[i]. V opačnom prípade ignorujeme aktuálny prvok.  
  pivot: end -= 1 # Ak sa začiatok a koniec neprekrížili, # vymeňte čísla na začiatku a na konci, ak(začiatok < end): array[start], array[end] = array[end], array[start] # Swap pivot element with element on end pointer. # This puts pivot on its correct sorted place. array[end], array[pivot_index] = array[pivot_index], array[end] # Returning end pointer to divide the array into 2 return end # The main function that implements QuickSort def quick_sort(start, end, array): if (start  < end): # p is partitioning index, array[p] # is at right place p = partition(start, end, array) # Sort elements before partition # and after partition quick_sort(start, p - 1, array) quick_sort(p + 1, end, array) # Driver code array = [ 10, 7, 8, 9, 1, 5 ] quick_sort(0, len(array) - 1, array) print(f'Sorted array: {array}') 

Sorted array: [1, 5, 7, 8, 9, 10] 

Časová zložitosť: O(n(logn))

ShellSort

ShellSort je hlavne variáciou zoradenia vloženia. Pri triedení vkladania presúvame prvky iba o jednu pozíciu dopredu. Keď sa prvok musí posunúť ďaleko dopredu, je to veľa pohybov. Myšlienkou shellSort je umožniť výmenu vzdialených predmetov. V shellSort urobíme pole h-triedené pre veľkú hodnotu h. Neustále znižujeme hodnotu h, kým sa nestane 1. Pole sa nazýva h-triedené, ak všetky podzoznamy každého h ^th prvok je zoradený.

# Python3 program for implementation of Shell Sort def shellSort(arr): gap = len(arr) // 2 # initialize the gap while gap>0: i = 0 j = medzera # skontrolujte pole zľava doprava # až po posledný možný index j, zatiaľ čo j < len(arr): if arr[i]>arr[j]: arr[i],arr[j] = arr[j],arr[i] i += 1 j += 1 # teraz sa pozrieme späť od i-tého indexu doľava # vymeníme hodnoty, ktoré nie sú v správnom poradí. k = i, zatiaľ čo k - medzera> -1: ak arr[k - medzera]> arr[k]: arr[k-medzera],arr[k] = arr[k],arr[k-medzera] k -= 1 medzera //= 2 # ovládač na kontrolu kódu arr2 = [12, 34, 54, 2, 3] print('vstupné pole:',arr2) shellSort(arr2) print('triedené pole', arr2) 

input array: [12, 34, 54, 2, 3] sorted array [2, 3, 12, 34, 54] 

Časová zložitosť: O(n ² ).