LCA pre n-árny strom | Konštantný dopyt O(1)
Videli sme rôzne metódy s rôznou časovou zložitosťou na výpočet LCA v n-árnom strome: -
Metóda 1: Naivná metóda (vypočítaním cesty od koreňa k uzlu) | O(n) na dotaz
Metóda 2: Použitie rozkladu Sqrt | O(sqrt H)
Metóda 3: Použitie prístupu riedkej matice DP | O(logn)
Poďme študovať inú metódu, ktorá má rýchlejší čas dotazu ako všetky vyššie uvedené metódy. Naším cieľom teda bude vypočítať LCA v konštantný čas ~ O(1) . Pozrime sa, ako to môžeme dosiahnuť.
Metóda 4: Použitie dotazu na minimálny rozsah
Diskutovali sme LCA a RMQ pre binárny strom . Tu diskutujeme o konverzii problému LCA na problém RMQ pre n-árny strom.
Pre-requisites:- LCA in Binary Tree using RMQ RMQ using sparse table
Kľúčový koncept: V tejto metóde zredukujeme náš problém LCA na problém RMQ (Minimálny rozsah dopytu) cez statické pole. Keď to urobíme, spojíme dopyty minimálneho rozsahu s požadovanými dopytmi LCA.
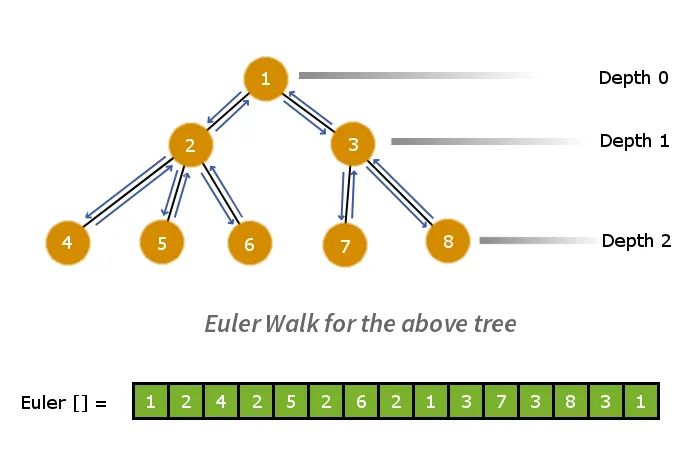
Prvým krokom bude rozloženie stromu na ploché lineárne pole. Na to môžeme použiť Eulerovu chôdzu. Eulerova chôdza poskytne predobjednávkový prechod grafu. Takže vykonáme Eulerovu prechádzku na strome a uložíme uzly do poľa, keď ich navštívime. Tento proces redukuje strom > 
Teraz sa zamyslime všeobecne: Zvážte akékoľvek dva uzly na strome. Bude existovať presne jedna cesta spájajúca oba uzly a uzol, ktorý má najmenšiu hodnotu hĺbky v ceste, bude LCA dvoch daných uzlov.
Teraz povedzme akékoľvek dva odlišné uzly v a v v Eulerovom prechádzkovom poli. Teraz budú všetky prvky na ceste od u do v ležať medzi indexom uzlov u a v v Eulerovom poli chôdze. Preto stačí vypočítať uzol s minimálnou hĺbkou medzi indexom uzla u a uzlom v v Eulerovom poli.
Na tento účel budeme udržiavať ďalšie pole, ktoré bude obsahovať hĺbku všetkých uzlov zodpovedajúcich ich polohe v poli Euler walk, aby sme naň mohli použiť náš algoritmus RMQ.
Nižšie je uvedené eulerovo prechádzkové pole paralelné s jeho hĺbkovým poľom.

Príklad: Uvažujme dva uzly uzol 6 a uzol 7 v eulerovom poli. Na výpočet LCA uzla 6 a uzla 7 hľadáme najmenšiu hodnotu hĺbky pre všetky uzly medzi uzlom 6 a uzlom 7.
Preto uzol 1 má najmenšiu hodnota hĺbky = 0 a teda je to LCA pre uzol 6 a uzol 7.

Implementácia: -
We will be maintaining three arrays 1) Euler Path 2) Depth array 3) First Appearance Index
Pole Euler Path a Depth sú rovnaké, ako je opísané vyššie
Index prvého vzhľadu FAI[] : Pole indexu prvého vzhľadu uloží index pre prvú pozíciu každého uzla v poli Euler Path. FAI[i] = Prvý výskyt i-tého uzla v poli Euler Walk.
Implementácia vyššie uvedenej metódy je uvedená nižšie:
Implementácia:
C++ // C++ program to demonstrate LCA of n-ary tree // in constant time. #include 'bits/stdc++.h' using namespace std ; #define sz 101 vector < int > adj [ sz ]; // stores the tree vector < int > euler ; // tracks the eulerwalk vector < int > depthArr ; // depth for each node corresponding // to eulerwalk int FAI [ sz ]; // stores first appearance index of every node int level [ sz ]; // stores depth for all nodes in the tree int ptr ; // pointer to euler walk int dp [ sz ][ 18 ]; // sparse table int logn [ sz ]; // stores log values int p2 [ 20 ]; // stores power of 2 void buildSparseTable ( int n ) { // initializing sparse table memset ( dp -1 sizeof ( dp )); // filling base case values for ( int i = 1 ; i < n ; i ++ ) dp [ i -1 ][ 0 ] = ( depthArr [ i ] > depthArr [ i -1 ]) ? i -1 : i ; // dp to fill sparse table for ( int l = 1 ; l < 15 ; l ++ ) for ( int i = 0 ; i < n ; i ++ ) if ( dp [ i ][ l -1 ] != -1 and dp [ i + p2 [ l -1 ]][ l -1 ] != -1 ) dp [ i ][ l ] = ( depthArr [ dp [ i ][ l -1 ]] > depthArr [ dp [ i + p2 [ l -1 ]][ l -1 ]]) ? dp [ i + p2 [ l -1 ]][ l -1 ] : dp [ i ][ l -1 ]; else break ; } int query ( int l int r ) { int d = r - l ; int dx = logn [ d ]; if ( l == r ) return l ; if ( depthArr [ dp [ l ][ dx ]] > depthArr [ dp [ r - p2 [ dx ]][ dx ]]) return dp [ r - p2 [ dx ]][ dx ]; else return dp [ l ][ dx ]; } void preprocess () { // memorizing powers of 2 p2 [ 0 ] = 1 ; for ( int i = 1 ; i < 18 ; i ++ ) p2 [ i ] = p2 [ i -1 ] * 2 ; // memorizing all log(n) values int val = 1 ptr = 0 ; for ( int i = 1 ; i < sz ; i ++ ) { logn [ i ] = ptr -1 ; if ( val == i ) { val *= 2 ; logn [ i ] = ptr ; ptr ++ ; } } } /** * Euler Walk ( preorder traversal) * converting tree to linear depthArray * Time Complexity : O(n) * */ void dfs ( int cur int prev int dep ) { // marking FAI for cur node if ( FAI [ cur ] == -1 ) FAI [ cur ] = ptr ; level [ cur ] = dep ; // pushing root to euler walk euler . push_back ( cur ); // incrementing euler walk pointer ptr ++ ; for ( auto x : adj [ cur ]) { if ( x != prev ) { dfs ( x cur dep + 1 ); // pushing cur again in backtrack // of euler walk euler . push_back ( cur ); // increment euler walk pointer ptr ++ ; } } } // Create Level depthArray corresponding // to the Euler walk Array void makeArr () { for ( auto x : euler ) depthArr . push_back ( level [ x ]); } int LCA ( int u int v ) { // trivial case if ( u == v ) return u ; if ( FAI [ u ] > FAI [ v ]) swap ( u v ); // doing RMQ in the required range return euler [ query ( FAI [ u ] FAI [ v ])]; } void addEdge ( int u int v ) { adj [ u ]. push_back ( v ); adj [ v ]. push_back ( u ); } int main ( int argc char const * argv []) { // constructing the described tree int numberOfNodes = 8 ; addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 2 4 ); addEdge ( 2 5 ); addEdge ( 2 6 ); addEdge ( 3 7 ); addEdge ( 3 8 ); // performing required precalculations preprocess (); // doing the Euler walk ptr = 0 ; memset ( FAI -1 sizeof ( FAI )); dfs ( 1 0 0 ); // creating depthArray corresponding to euler[] makeArr (); // building sparse table buildSparseTable ( depthArr . size ()); cout < < 'LCA(67) : ' < < LCA ( 6 7 ) < < ' n ' ; cout < < 'LCA(64) : ' < < LCA ( 6 4 ) < < ' n ' ; return 0 ; }
Java // Java program to demonstrate LCA of n-ary // tree in constant time. import java.util.ArrayList ; import java.util.Arrays ; class GFG { static int sz = 101 ; @SuppressWarnings ( 'unchecked' ) // Stores the tree static ArrayList < Integer >[] adj = new ArrayList [ sz ] ; // Tracks the eulerwalk static ArrayList < Integer > euler = new ArrayList <> (); // Depth for each node corresponding static ArrayList < Integer > depthArr = new ArrayList <> (); // to eulerwalk // Stores first appearance index of every node static int [] FAI = new int [ sz ] ; // Stores depth for all nodes in the tree static int [] level = new int [ sz ] ; // Pointer to euler walk static int ptr ; // Sparse table static int [][] dp = new int [ sz ][ 18 ] ; // Stores log values static int [] logn = new int [ sz ] ; // Stores power of 2 static int [] p2 = new int [ 20 ] ; static void buildSparseTable ( int n ) { // Initializing sparse table for ( int i = 0 ; i < sz ; i ++ ) { for ( int j = 0 ; j < 18 ; j ++ ) { dp [ i ][ j ] = - 1 ; } } // Filling base case values for ( int i = 1 ; i < n ; i ++ ) dp [ i - 1 ][ 0 ] = ( depthArr . get ( i ) > depthArr . get ( i - 1 )) ? i - 1 : i ; // dp to fill sparse table for ( int l = 1 ; l < 15 ; l ++ ) for ( int i = 0 ; i < n ; i ++ ) if ( dp [ i ][ l - 1 ] != - 1 && dp [ i + p2 [ l - 1 ]][ l - 1 ] != - 1 ) dp [ i ][ l ] = ( depthArr . get ( dp [ i ][ l - 1 ] ) > depthArr . get ( dp [ i + p2 [ l - 1 ]][ l - 1 ] )) ? dp [ i + p2 [ l - 1 ]][ l - 1 ] : dp [ i ][ l - 1 ] ; else break ; } static int query ( int l int r ) { int d = r - l ; int dx = logn [ d ] ; if ( l == r ) return l ; if ( depthArr . get ( dp [ l ][ dx ] ) > depthArr . get ( dp [ r - p2 [ dx ]][ dx ] )) return dp [ r - p2 [ dx ]][ dx ] ; else return dp [ l ][ dx ] ; } static void preprocess () { // Memorizing powers of 2 p2 [ 0 ] = 1 ; for ( int i = 1 ; i < 18 ; i ++ ) p2 [ i ] = p2 [ i - 1 ] * 2 ; // Memorizing all log(n) values int val = 1 ptr = 0 ; for ( int i = 1 ; i < sz ; i ++ ) { logn [ i ] = ptr - 1 ; if ( val == i ) { val *= 2 ; logn [ i ] = ptr ; ptr ++ ; } } } // Euler Walk ( preorder traversal) converting // tree to linear depthArray // Time Complexity : O(n) static void dfs ( int cur int prev int dep ) { // Marking FAI for cur node if ( FAI [ cur ] == - 1 ) FAI [ cur ] = ptr ; level [ cur ] = dep ; // Pushing root to euler walk euler . add ( cur ); // Incrementing euler walk pointer ptr ++ ; for ( Integer x : adj [ cur ] ) { if ( x != prev ) { dfs ( x cur dep + 1 ); // Pushing cur again in backtrack // of euler walk euler . add ( cur ); // Increment euler walk pointer ptr ++ ; } } } // Create Level depthArray corresponding // to the Euler walk Array static void makeArr () { for ( Integer x : euler ) depthArr . add ( level [ x ] ); } static int LCA ( int u int v ) { // Trivial case if ( u == v ) return u ; if ( FAI [ u ] > FAI [ v ] ) { int temp = u ; u = v ; v = temp ; } // Doing RMQ in the required range return euler . get ( query ( FAI [ u ] FAI [ v ] )); } static void addEdge ( int u int v ) { adj [ u ] . add ( v ); adj [ v ] . add ( u ); } // Driver code public static void main ( String [] args ) { for ( int i = 0 ; i < sz ; i ++ ) { adj [ i ] = new ArrayList <> (); } // Constructing the described tree int numberOfNodes = 8 ; addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 2 4 ); addEdge ( 2 5 ); addEdge ( 2 6 ); addEdge ( 3 7 ); addEdge ( 3 8 ); // Performing required precalculations preprocess (); // Doing the Euler walk ptr = 0 ; Arrays . fill ( FAI - 1 ); dfs ( 1 0 0 ); // Creating depthArray corresponding to euler[] makeArr (); // Building sparse table buildSparseTable ( depthArr . size ()); System . out . println ( 'LCA(67) : ' + LCA ( 6 7 )); System . out . println ( 'LCA(64) : ' + LCA ( 6 4 )); } } // This code is contributed by sanjeev2552
Python3 # Python program to demonstrate LCA of n-ary tree # in constant time. from typing import List # stores the tree adj = [[] for _ in range ( 101 )] # tracks the eulerwalk euler = [] # depth for each node corresponding to eulerwalk depthArr = [] # stores first appearance index of every node FAI = [ - 1 ] * 101 # stores depth for all nodes in the tree level = [ 0 ] * 101 # pointer to euler walk ptr = 0 # sparse table dp = [[ - 1 ] * 18 for _ in range ( 101 )] # stores log values logn = [ 0 ] * 101 # stores power of 2 p2 = [ 0 ] * 20 def buildSparseTable ( n : int ): # initializing sparse table for i in range ( n ): dp [ i ][ 0 ] = i - 1 if depthArr [ i ] > depthArr [ i - 1 ] else i # dp to fill sparse table for l in range ( 1 15 ): for i in range ( n ): if dp [ i ][ l - 1 ] != - 1 and dp [ i + p2 [ l - 1 ]][ l - 1 ] != - 1 : dp [ i ][ l ] = dp [ i + p2 [ l - 1 ]][ l - 1 ] if depthArr [ dp [ i ][ l - 1 ] ] > depthArr [ dp [ i + p2 [ l - 1 ]][ l - 1 ]] else dp [ i ][ l - 1 ] else : break def query ( l : int r : int ) -> int : d = r - l dx = logn [ d ] if l == r : return l if depthArr [ dp [ l ][ dx ]] > depthArr [ dp [ r - p2 [ dx ]][ dx ]]: return dp [ r - p2 [ dx ]][ dx ] else : return dp [ l ][ dx ] def preprocess (): global ptr # memorizing powers of 2 p2 [ 0 ] = 1 for i in range ( 1 18 ): p2 [ i ] = p2 [ i - 1 ] * 2 # memorizing all log(n) values val = 1 ptr = 0 for i in range ( 1 101 ): logn [ i ] = ptr - 1 if val == i : val *= 2 logn [ i ] = ptr ptr += 1 def dfs ( cur : int prev : int dep : int ): global ptr # marking FAI for cur node if FAI [ cur ] == - 1 : FAI [ cur ] = ptr level [ cur ] = dep # pushing root to euler walk euler . append ( cur ) # incrementing euler walk pointer ptr += 1 for x in adj [ cur ]: if x != prev : dfs ( x cur dep + 1 ) # pushing cur again in backtrack # of euler walk euler . append ( cur ) # increment euler walk pointer ptr += 1 # Create Level depthArray corresponding # to the Euler walk Array def makeArr (): global depthArr for x in euler : depthArr . append ( level [ x ]) def LCA ( u : int v : int ) -> int : # trivial case if u == v : return u if FAI [ u ] > FAI [ v ]: u v = v u # doing RMQ in the required range return euler [ query ( FAI [ u ] FAI [ v ])] def addEdge ( u v ): adj [ u ] . append ( v ) adj [ v ] . append ( u ) # constructing the described tree numberOfNodes = 8 addEdge ( 1 2 ) addEdge ( 1 3 ) addEdge ( 2 4 ) addEdge ( 2 5 ) addEdge ( 2 6 ) addEdge ( 3 7 ) addEdge ( 3 8 ) # performing required precalculations preprocess () # doing the Euler walk ptr = 0 FAI = [ - 1 ] * ( numberOfNodes + 1 ) dfs ( 1 0 0 ) # creating depthArray corresponding to euler[] makeArr () # building sparse table buildSparseTable ( len ( depthArr )) print ( 'LCA(67) : ' LCA ( 6 7 )) print ( 'LCA(64) : ' LCA ( 6 4 ))
C# // C# program to demonstrate LCA of n-ary // tree in constant time. using System ; using System.Collections.Generic ; public class GFG { static int sz = 101 ; // Stores the tree static List < int > [] adj = new List < int > [ sz ]; // Tracks the eulerwalk static List < int > euler = new List < int > (); // Depth for each node corresponding static List < int > depthArr = new List < int > (); // to eulerwalk // Stores first appearance index of every node static int [] FAI = new int [ sz ]; // Stores depth for all nodes in the tree static int [] level = new int [ sz ]; // Pointer to euler walk static int ptr ; // Sparse table static int [] dp = new int [ sz 18 ]; // Stores log values static int [] logn = new int [ sz ]; // Stores power of 2 static int [] p2 = new int [ 20 ]; static void buildSparseTable ( int n ) { // Initializing sparse table for ( int i = 0 ; i < sz ; i ++ ) { for ( int j = 0 ; j < 18 ; j ++ ) { dp [ i j ] = - 1 ; } } // Filling base case values for ( int i = 1 ; i < n ; i ++ ) dp [ i - 1 0 ] = ( depthArr [ i ] > depthArr [ i - 1 ]) ? i - 1 : i ; // dp to fill sparse table for ( int l = 1 ; l < 15 ; l ++ ) for ( int i = 0 ; i < n ; i ++ ) if ( dp [ i l - 1 ] != - 1 && dp [ i + p2 [ l - 1 ] l - 1 ] != - 1 ) dp [ i l ] = ( depthArr [ dp [ i l - 1 ]] > depthArr [ dp [ i + p2 [ l - 1 ] l - 1 ]]) ? dp [ i + p2 [ l - 1 ] l - 1 ] : dp [ i l - 1 ]; else break ; } static int query ( int l int r ) { int d = r - l ; int dx = logn [ d ]; if ( l == r ) return l ; if ( depthArr [ dp [ l dx ]] > depthArr [ dp [ r - p2 [ dx ] dx ]]) return dp [ r - p2 [ dx ] dx ]; else return dp [ l dx ]; } static void preprocess () { // Memorizing powers of 2 p2 [ 0 ] = 1 ; for ( int i = 1 ; i < 18 ; i ++ ) p2 [ i ] = p2 [ i - 1 ] * 2 ; // Memorizing all log(n) values int val = 1 ptr = 0 ; for ( int i = 1 ; i < sz ; i ++ ) { logn [ i ] = ptr - 1 ; if ( val == i ) { val *= 2 ; logn [ i ] = ptr ; ptr ++ ; } } } // Euler Walk ( preorder traversal) converting // tree to linear depthArray // Time Complexity : O(n) static void dfs ( int cur int prev int dep ) { // Marking FAI for cur node if ( FAI [ cur ] == - 1 ) FAI [ cur ] = ptr ; level [ cur ] = dep ; // Pushing root to euler walk euler . Add ( cur ); // Incrementing euler walk pointer ptr ++ ; foreach ( int x in adj [ cur ]) { if ( x != prev ) { dfs ( x cur dep + 1 ); euler . Add ( cur ); ptr ++ ; } } } // Create Level depthArray corresponding // to the Euler walk Array static void makeArr () { foreach ( int x in euler ) depthArr . Add ( level [ x ]); } static int LCA ( int u int v ) { // Trivial case if ( u == v ) return u ; if ( FAI [ u ] > FAI [ v ]) { int temp = u ; u = v ; v = temp ; } // Doing RMQ in the required range return euler [ query ( FAI [ u ] FAI [ v ])]; } static void addEdge ( int u int v ) { adj [ u ]. Add ( v ); adj [ v ]. Add ( u ); } // Driver Code static void Main ( string [] args ) { int sz = 9 ; adj = new List < int > [ sz ]; for ( int i = 0 ; i < sz ; i ++ ) { adj [ i ] = new List < int > (); } // Constructing the described tree int numberOfNodes = 8 ; addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 2 4 ); addEdge ( 2 5 ); addEdge ( 2 6 ); addEdge ( 3 7 ); addEdge ( 3 8 ); // Performing required precalculations preprocess (); // Doing the Euler walk ptr = 0 ; Array . Fill ( FAI - 1 ); dfs ( 1 0 0 ); // Creating depthArray corresponding to euler[] makeArr (); // Building sparse table buildSparseTable ( depthArr . Count ); Console . WriteLine ( 'LCA(67) : ' + LCA ( 6 7 )); Console . WriteLine ( 'LCA(64) : ' + LCA ( 6 4 )); } } // This code is contributed by Prince Kumar
JavaScript let adj = []; for ( let _ = 0 ; _ < 101 ; _ ++ ) { adj . push ([]); } // tracks the eulerwalk let euler = []; // depth for each node corresponding to eulerwalk let depthArr = []; // stores first appearance index of every node let FAI = new Array ( 101 ). fill ( - 1 ); // stores depth for all nodes in the tree let level = new Array ( 101 ). fill ( 0 ); // pointer to euler walk let ptr = 0 ; // sparse table let dp = []; for ( let _ = 0 ; _ < 101 ; _ ++ ) { dp . push ( new Array ( 18 ). fill ( - 1 )); } // stores log values let logn = new Array ( 101 ). fill ( 0 ); // stores power of 2 let p2 = new Array ( 20 ). fill ( 0 ); function buildSparseTable ( n ) { // initializing sparse table for ( let i = 0 ; i < n ; i ++ ) { dp [ i ][ 0 ] = i - 1 >= 0 && depthArr [ i ] > depthArr [ i - 1 ] ? i - 1 : i ; } // dp to fill sparse table for ( let l = 1 ; l < 15 ; l ++ ) { for ( let i = 0 ; i < n ; i ++ ) { if ( dp [ i ][ l - 1 ] !== - 1 && dp [ i + p2 [ l - 1 ]][ l - 1 ] !== - 1 ) { dp [ i ][ l ] = depthArr [ dp [ i ][ l - 1 ]] > depthArr [ dp [ i + p2 [ l - 1 ]][ l - 1 ]] ? dp [ i + p2 [ l - 1 ]][ l - 1 ] : dp [ i ][ l - 1 ]; } else { break ; } } } } function query ( l r ) { let d = r - l ; let dx = logn [ d ]; if ( l === r ) { return l ; } if ( depthArr [ dp [ l ][ dx ]] > depthArr [ dp [ r - p2 [ dx ]][ dx ]]) { return dp [ r - p2 [ dx ]][ dx ]; } else { return dp [ l ][ dx ]; } } function preprocess () { // memorizing powers of 2 p2 [ 0 ] = 1 ; for ( let i = 1 ; i < 18 ; i ++ ) { p2 [ i ] = p2 [ i - 1 ] * 2 ; } // memorizing all log(n) values let val = 1 ; ptr = 0 ; for ( let i = 1 ; i < 101 ; i ++ ) { logn [ i ] = ptr - 1 ; if ( val === i ) { val *= 2 ; logn [ i ] = ptr ; ptr += 1 ; } } } function dfs ( cur prev dep ) { // marking FAI for cur node if ( FAI [ cur ] === - 1 ) { FAI [ cur ] = ptr ; } level [ cur ] = dep ; // pushing root to euler walk euler . push ( cur ); // incrementing euler walk pointer ptr += 1 ; for ( let x of adj [ cur ]) { if ( x !== prev ) { dfs ( x cur dep + 1 ); // pushing cur again in backtrack // of euler walk euler . push ( cur ); // increment euler walk pointer ptr += 1 ; } } } // Create Level depthArray corresponding // to the Euler walk Array function makeArr () { for ( let x of euler ) { depthArr . push ( level [ x ]); } } function LCA ( u v ) { // trivial case if ( u === v ) { return u ; } if ( FAI [ u ] > FAI [ v ]) { [ u v ] = [ v u ]; } // doing RMQ in the required range return euler [ query ( FAI [ u ] FAI [ v ])]; } function addEdge ( u v ) { adj [ u ]. push ( v ); adj [ v ]. push ( u ); } // constructing the described tree let numberOfNodes = 8 ; addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 2 4 ); addEdge ( 2 5 ); addEdge ( 2 6 ); addEdge ( 3 7 ); addEdge ( 3 8 ); // performing required precalculations preprocess (); // doing the Euler walk ptr = 0 ; FAI = new Array ( numberOfNodes + 1 ). fill ( - 1 ); dfs ( 1 0 0 ); // creating depthArray corresponding to euler[] makeArr (); // building sparse table buildSparseTable ( depthArr . length ); console . log ( 'LCA(67) : ' LCA ( 6 7 )); console . log ( 'LCA(64) : ' LCA ( 6 4 ));
Výstup
LCA(67) : 1 LCA(64) : 2
Poznámka: Predbežne vypočítavame všetky požadované mocniny 2 a tiež predbežne vypočítavame všetky požadované hodnoty protokolu, aby sme zabezpečili konštantnú časovú zložitosť na dotaz. V opačnom prípade, ak by sme vykonali výpočet protokolu pre každú operáciu dotazu, naša časová zložitosť by nebola konštantná.
Časová zložitosť: Proces konverzie z LCA na RMQ vykonáva Euler Walk, ktorý trvá O(n) čas.
Predspracovanie pre riedku tabuľku v RMQ trvá O(nlogn) čas a zodpovedanie každého dotazu je proces s konštantným časom. Celková časová zložitosť je teda O(nlogn) - predspracovanie a O(1) pre každý dotaz.
Pomocný priestor: O(n+s)
Vytvoriť kvíz