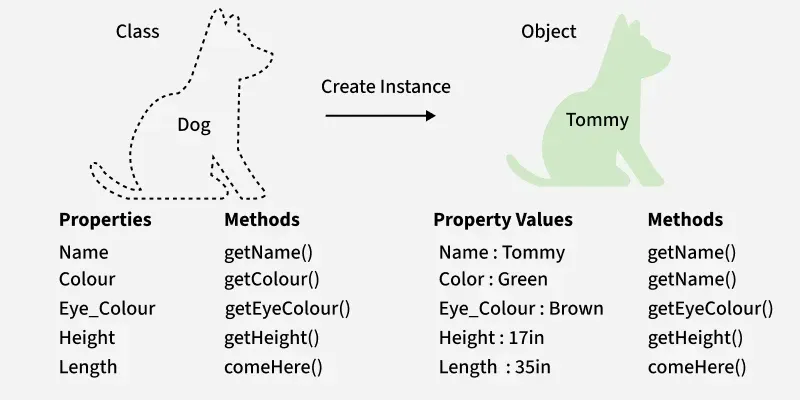
Ford-Fulkersonov algoritmus je široko používaný algoritmus na riešenie problému maximálneho toku v tokovej sieti. Problém maximálneho toku zahŕňa určenie maximálneho množstva toku, ktorý možno poslať zo zdrojového vrcholu do klesajúceho vrcholu v nasmerovanom váženom grafe, s výhradou kapacitných obmedzení na okrajoch.

Algoritmus funguje tak, že iteratívnym spôsobom hľadá rozširujúcu cestu, čo je cesta od zdroja k záchytu v zvyškovom grafe, t. j. graf získaný odčítaním toku prúdu od kapacity každej hrany. Algoritmus potom zvýši tok pozdĺž tejto dráhy o maximálne možné množstvo, čo je minimálna kapacita hrán pozdĺž dráhy.

problém:

Daný graf, ktorý predstavuje sieť tokov, kde každá hrana má kapacitu. Tiež vzhľadom na dva vrcholy zdroj „s“ a drez „t“ v grafe nájdite maximálny možný prietok od s do t s nasledujúcimi obmedzeniami:

• Prietok na hrane nepresahuje danú kapacitu hrany.
• Prichádzajúci tok sa rovná odchádzajúcemu toku pre každý vrchol okrem s a t.

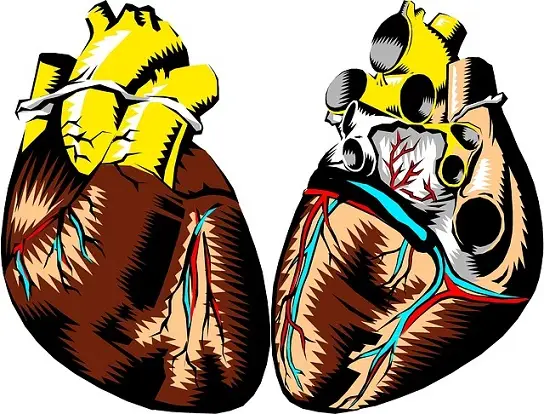
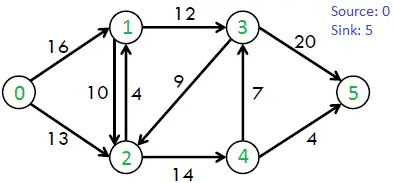
Uvažujme napríklad o nasledujúcom grafe z knihy CLRS.

Maximálny možný prietok vo vyššie uvedenom grafe je 23.

Odporúčaný postup Nájdite maximálny prietok Vyskúšajte to!

Predpoklad: Úvod do problému maximálneho prietoku

Ford-Fulkersonov algoritmus

Nasleduje jednoduchá myšlienka Ford-Fulkersonovho algoritmu:

1. Začnite s počiatočným tokom ako 0.
2. Zatiaľ čo existuje rozširujúca cesta od zdroja k umývadlu:
   • Nájdite rozširujúcu cestu pomocou ľubovoľného algoritmu hľadania cesty, ako je vyhľadávanie do šírky alebo do hĺbky.
   • Určte množstvo toku, ktorý možno poslať pozdĺž zväčšujúcej cesty, čo je minimálna zvyšková kapacita pozdĺž okrajov cesty.
   • Zvýšte prietok pozdĺž zväčšovacej dráhy o určené množstvo.
3. Vráťte maximálny prietok.

Časová zložitosť: Časová zložitosť vyššie uvedeného algoritmu je O(max_flow * E). Spustíme slučku, kým existuje rozširujúca cesta. V najhoršom prípade môžeme pridať 1 tok jednotky v každej iterácii. Preto sa časová zložitosť stáva O(max_flow * E).

Ako implementovať vyššie uvedený jednoduchý algoritmus?
Najprv definujme koncept reziduálneho grafu, ktorý je potrebný na pochopenie implementácie.

Reziduálny graf prietokovej siete je graf, ktorý ukazuje ďalší možný prietok. Ak v reziduálnom grafe existuje cesta od zdroja k ponoru, potom je možné pridať prietok. Každá hrana zvyškového grafu má hodnotu tzv zvyšková kapacita čo sa rovná pôvodnej kapacite hrany mínus prietok prúdu. Zvyšková kapacita je v podstate aktuálna kapacita hrany.

Poďme sa teraz porozprávať o detailoch implementácie. Zvyšková kapacita je 0, ak medzi dvoma vrcholmi zvyškového grafu nie je žiadna hrana. Môžeme inicializovať zvyškový graf ako pôvodný graf, pretože neexistuje žiadny počiatočný tok a počiatočná zvyšková kapacita sa rovná pôvodnej kapacite. Aby sme našli rozširujúcu cestu, môžeme buď urobiť BFS alebo DFS zvyškového grafu. Použili sme BFS v nižšie uvedenej implementácii. Pomocou BFS môžeme zistiť, či existuje cesta od zdroja k ponoru. BFS tiež vytvára nadradené[] pole. Pomocou poľa parent[] prechádzame cez nájdenú cestu a nájdeme možný prietok touto cestou nájdením minimálnej zvyškovej kapacity pozdĺž cesty. Neskôr pridáme tok nájdenej cesty k celkovému toku.

Dôležité je, že musíme aktualizovať zvyškové kapacity v grafe zvyškov. Odčítame tok cesty od všetkých hrán pozdĺž cesty a pridáme tok cesty pozdĺž reverzných hrán Potrebujeme pridať tok cesty pozdĺž reverzných hrán, pretože neskôr možno bude potrebné poslať tok v opačnom smere (pozri napríklad nasledujúci odkaz).

Nižšie je uvedená implementácia Ford-Fulkersonovho algoritmu. Aby to bolo jednoduché, graf je reprezentovaný ako 2D matica.

C++

// C++ program for implementation of Ford Fulkerson> // algorithm> #include> #include> #include> #include> using> namespace> std;> // Number of vertices in given graph> #define V 6> /* Returns true if there is a path from source 's' to sink> > 't' in residual graph. Also fills parent[] to store the> > path */> bool> bfs(> int> rGraph[V][V],> int> s,> int> t,> int> parent[])> {> > // Create a visited array and mark all vertices as not> > // visited> > bool> visited[V];> > memset> (visited, 0,> sizeof> (visited));> > // Create a queue, enqueue source vertex and mark source> > // vertex as visited> > queue <> int> >q;> > q.push(s);> > visited[s] => true> ;> > parent[s] = -1;> > // Standard BFS Loop> > while> (!q.empty()) {> > int> u = q.front();> > q.pop();> > for> (> int> v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Ak nájdeme spojenie so sink uzlom, // potom už BFS nemá zmysel Musíme // len nastaviť jeho rodiča a môžeme vrátiť // true if (v == t) { parent[ v] = u; vrátiť true; } q.push(v); rodič[v] = u; navštívené[v] = pravda; } } } // Nedosiahli sme sink v BFS počnúc zdrojom, takže // vráti false return false; } // Vráti maximálny prietok od s do t v danom grafe int fordFulkerson(int graf[V][V], int s, int t) { int u, v; // Vytvorte zvyškový graf a vyplňte zvyškový graf // danými kapacitami v pôvodnom grafe ako // zvyškovými kapacitami v zvyškovom grafe int rGraph[V] [V]; // Zvyškový graf kde rGraph[i][j] // označuje zvyškovú kapacitu hrany // od i do j (ak existuje hrana. Ak // rGraph[i][j] je 0, tak nie je) for (u = 0; u for (v = 0; v rGraph[u][v] = graf[u][v]; int parent[V]; // Toto pole vyplní BFS a // uloží cestu int max_flow = 0 // Na začiatku nie je žiadny tok // Rozšírte tok, kým existuje cesta od zdroja k // klesnutiu while (bfs(rGraph, s, t, parent)) { // Nájdite minimálnu zvyškovú kapacitu hrán pozdĺž // cesty vyplnenej BFS Alebo môžeme povedať, že nájdeš // maximálny prietok cez nájdenú cestu int cesta_tok = INT_MAX pre (v = t; v != s; v = rodič[v]) { u = parent[v]; cesta_tok = min(cesta_tok, rGraf[u][v] } // aktualizácia zvyškových kapacít hrán a // obrátenie hrán pozdĺž cesty pre (v = t; v != s; v =); rodič[v]) { u = rodič[v]; rGraph[u][v] -= tok_cesty; // Vráti celkový tok return max_flow; } // Program ovládača na testovanie vyššie uvedených funkcií int main() { // Vytvorme graf zobrazený vo vyššie uvedenom príklade int graf[V][V] = { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7 , 0, 4}, { 0, 0, 0, 0, 0, 0}}; cout < < 'The maximum possible flow is ' < < fordFulkerson(graph, 0, 5); return 0; }>

Java

// Java program for implementation of Ford Fulkerson> // algorithm> import> java.io.*;> import> java.lang.*;> import> java.util.*;> import> java.util.LinkedList;> class> MaxFlow {> > static> final> int> V => 6> ;> // Number of vertices in graph> > /* Returns true if there is a path from source 's' to> > sink 't' in residual graph. Also fills parent[] to> > store the path */> > boolean> bfs(> int> rGraph[][],> int> s,> int> t,> int> parent[])> > {> > // Create a visited array and mark all vertices as> > // not visited> > boolean> visited[] => new> boolean> [V];> > for> (> int> i => 0> ; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited LinkedList queue = new LinkedList(); queue.add(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.size() != 0) { int u = queue.poll(); for (int v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Ak nájdeme spojenie so sink // uzlom, potom v BFS už nemá zmysel // Len musíme nastaviť jeho rodiča // a môžeme vrátiť true if (v == t) { parent[ v] = u; vrátiť true; } queue.add(v); rodič[v] = u; navštívené[v] = pravda; } } } // Nedosiahli sme klesnutie v BFS počnúc zdrojom, // takže return false return false; } // Vráti maximálny prietok od s do t v danom // grafe int fordFulkerson(int graf[][], int s, int t) { int u, v; // Vytvorte zvyškový graf a vyplňte zvyškový // graf danými kapacitami v pôvodnom grafe // ako zvyškové kapacity v grafe zvyškov // Zvyškový graf kde rGraph[i][j] označuje // zvyškovú kapacitu hrany od i do j (ak je tam // hrana. Ak rGraph[i][j] je 0, tak tam // nie je) int rGraph[][] = new int[V][V]; for (u = 0; u for (v = 0; v rGraph[u][v] = graf[u][v]; // Toto pole je vyplnené BFS a na uloženie cesty int parent[] = new int[ V] int max_flow = 0 // Na začiatku nie je žiadny tok // Rozšírte tok, kým existuje cesta zo zdroja // do klesania while (bfs(rGraph, s, t, rodič)) { // Nájdite minimálnu zvyškovú kapacitu; hrán // po ceste vyplnenej BFS Alebo môžeme povedať // nájsť maximálny prietok cez nájdenú cestu int cesta_tok = Integer.MAX_VALUE for (v = t; v != s; v = parent[v ]) { u = parent[v]; cesta_tok = Math.min(cesta_tok, rGraf[u][v] } // aktualizácia zvyškových kapacít hrán a // obrátenie hrán pozdĺž cesty pre (v = t; v != s; v = rodič[v]) { u = rodič[v]; rGraph[u][v] -= tok_cesty[v][u] += tok_cesty } // Pridanie toku cesty do celkovej; flow max_flow += cesta_tok } // Vráti celkový tok návrat max_flow } // Program ovládača na testovanie vyššie uvedených funkcií public static void main(String[] args) throws java.lang.Exception { // Vytvorme zobrazený graf; vo vyššie uvedenom príklade int graf[][] = new int[][] { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4 , 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7, 0, 4 }, { 0, 0, 0, 0, 0, 0 } }; MaxFlow m = new MaxFlow(); System.out.println('Maximálny možný prietok je ' + m.fordFulkerson(graf, 0, 5)); } }>

Python

# Python program for implementation> # of Ford Fulkerson algorithm> from> collections> import> defaultdict> # This class represents a directed graph> # using adjacency matrix representation> class> Graph:> > def> __init__(> self> , graph):> > self> .graph> => graph> # residual graph> > self> . ROW> => len> (graph)> > # self.COL = len(gr[0])> > '''Returns true if there is a path from source 's' to sink 't' in> > residual graph. Also fills parent[] to store the path '''> > def> BFS(> self> , s, t, parent):> > # Mark all the vertices as not visited> > visited> => [> False> ]> *> (> self> .ROW)> > # Create a queue for BFS> > queue> => []> > # Mark the source node as visited and enqueue it> > queue.append(s)> > visited[s]> => True> > # Standard BFS Loop> > while> queue:> > # Dequeue a vertex from queue and print it> > u> => queue.pop(> 0> )> > # Get all adjacent vertices of the dequeued vertex u> > # If a adjacent has not been visited, then mark it> > # visited and enqueue it> > for> ind, val> in> enumerate> (> self> .graph[u]):> > if> visited[ind]> => => False> and> val>> 0> :> > # If we find a connection to the sink node,> > # then there is no point in BFS anymore> > # We just have to set its parent and can return true> > queue.append(ind)> > visited[ind]> => True> > parent[ind]> => u> > if> ind> => => t:> > return> True> > # We didn't reach sink in BFS starting> > # from source, so return false> > return> False> > > > # Returns the maximum flow from s to t in the given graph> > def> FordFulkerson(> self> , source, sink):> > # This array is filled by BFS and to store path> > parent> => [> -> 1> ]> *> (> self> .ROW)> > max_flow> => 0> # There is no flow initially> > # Augment the flow while there is path from source to sink> > while> self> .BFS(source, sink, parent) :> > # Find minimum residual capacity of the edges along the> > # path filled by BFS. Or we can say find the maximum flow> > # through the path found.> > path_flow> => float> (> 'Inf'> )> > s> => sink> > while> (s !> => source):> > path_flow> => min> (path_flow,> self> .graph[parent[s]][s])> > s> => parent[s]> > # Add path flow to overall flow> > max_flow> +> => path_flow> > # update residual capacities of the edges and reverse edges> > # along the path> > v> => sink> > while> (v !> => source):> > u> => parent[v]> > self> .graph[u][v]> -> => path_flow> > self> .graph[v][u]> +> => path_flow> > v> => parent[v]> > return> max_flow> > # Create a graph given in the above diagram> graph> => [[> 0> ,> 16> ,> 13> ,> 0> ,> 0> ,> 0> ],> > [> 0> ,> 0> ,> 10> ,> 12> ,> 0> ,> 0> ],> > [> 0> ,> 4> ,> 0> ,> 0> ,> 14> ,> 0> ],> > [> 0> ,> 0> ,> 9> ,> 0> ,> 0> ,> 20> ],> > [> 0> ,> 0> ,> 0> ,> 7> ,> 0> ,> 4> ],> > [> 0> ,> 0> ,> 0> ,> 0> ,> 0> ,> 0> ]]> g> => Graph(graph)> source> => 0> ; sink> => 5> > print> (> 'The maximum possible flow is %d '> %> g.FordFulkerson(source, sink))> # This code is contributed by Neelam Yadav>

C#

// C# program for implementation> // of Ford Fulkerson algorithm> using> System;> using> System.Collections.Generic;> public> class> MaxFlow {> > static> readonly> int> V = 6;> // Number of vertices in> > // graph> > /* Returns true if there is a path> > from source 's' to sink 't' in residual> > graph. Also fills parent[] to store the> > path */> > bool> bfs(> int> [, ] rGraph,> int> s,> int> t,> int> [] parent)> > {> > // Create a visited array and mark> > // all vertices as not visited> > bool> [] visited => new> bool> [V];> > for> (> int> i = 0; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited List front = nový zoznam (); queue.Add(s); navštívené [s] = pravda; rodič [s] = -1; // Štandardná slučka BFS while (queue.Count != 0) { int u = queue[0]; queue.RemoveAt(0); for (int v = 0; v if (navštívené[v] == false && rGraph[u, v]> 0) { // Ak nájdeme spojenie so sink // uzlom, tak v BFS nemá zmysel / / už len musíme nastaviť jeho rodič // a môže vrátiť hodnotu true if (v == t) { parent[v] = u } queue.Add(v] = u; v] = true } // Nedosiahli sme klesanie v BFS od zdroja, // tak return false return false } // Vráti maximálny prietok // od s do t v danom grafe int fordFulkerson; (int[, ] graf, int s, int t) { int u, v // Vytvorte zvyškový graf a vyplňte // graf zvyškov danými // kapacitami v pôvodnom grafe ako // zvyškovými kapacitami v grafe zvyškov /; / Reziduálny graf kde rGraph[i,j] // označuje zvyškovú kapacitu // hrany od i do j (ak existuje // hrana. Ak je rGraph[i,j] 0, tak // nie je) int [, ] rGraph = new int[V, V] for (u = 0; u for (v = 0; v rGraph[u, v] = graf[u, v]; // Toto pole je vyplnené BFS a uložiť cestu int[] parent = new int[V]; int max_flow = 0; // Na začiatku nie je žiadny tok // Rozšírte tok, kým existuje cesta od zdroja // k poklesu while (bfs(rGraph, s, t, parent)) { // Nájdite minimálnu zvyškovú kapacitu hrán // pozdĺž cesty naplnené BFS. Alebo môžeme povedať // nájsť maximálny prietok cez nájdenú cestu. int cesta_tok = int.MaxValue; for (v = t; v != s; v = rodič[v]) { u = rodič[v]; cesta_tok = Math.Min(cesta_tok, rGraf[u, v]); } // aktualizácia zvyškových kapacít hrán a // obrátenie hrán pozdĺž cesty for (v = t; v != s; v = rodič[v]) { u = rodič[v]; rGraph[u, v] -= path_flow; rGraph[v, u] += tok_cesty; } // Pridanie toku cesty k celkovému toku max_flow += tok_cesty; } // Vráti celkový tok return max_flow; } // Kód ovládača public static void Main() { // Vytvorme graf zobrazený v príklade vyššie int[, ] graf = new int[, ] { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7 , 0, 4 }, { 0, 0, 0, 0, 0, 0 } }; MaxFlow m = new MaxFlow(); Console.WriteLine('Maximálny možný tok je ' + m.fordFulkerson(graf, 0, 5)); } } /* Tento kód prispel PrinceRaj1992 */>

Javascript

> // Javascript program for implementation of Ford> // Fulkerson algorithm> // Number of vertices in graph> let V = 6;> // Returns true if there is a path from source> // 's' to sink 't' in residual graph. Also> // fills parent[] to store the path> function> bfs(rGraph, s, t, parent)> {> > > // Create a visited array and mark all> > // vertices as not visited> > let visited => new> Array(V);> > for> (let i = 0; i visited[i] = false; // Create a queue, enqueue source vertex // and mark source vertex as visited let queue = []; queue.push(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.length != 0) { let u = queue.shift(); for(let v = 0; v { if (visited[v] == false && rGraph[u][v]>0) { // Ak nájdeme spojenie so sink // uzlom, potom v BFS už nemá zmysel // Len musíme nastaviť jeho rodiča // a môžeme vrátiť true if (v == t) { parent[ v] = u; vrátiť true; } fronta.push(v); rodič[v] = u; navštívené[v] = pravda; } } } // Nedosiahli sme sink v BFS počnúc // zo zdroja, takže vráťte false return false; } // Vráti maximálny prietok od s do t v // danej grafovej funkcii fordFulkerson(graph, s, t) { nech u, v; // Vytvorte zvyškový graf a vyplňte // zvyškový graf danými kapacitami // v pôvodnom grafe ako zvyškové // kapacity v zvyškovom grafe // Zvyškový graf kde rGraph[i][j] // označuje zvyškovú kapacitu hrany // / od i do j (ak je tam hrana. // Ak je rGraph[i][j] 0, tak // nie je) nech rGraph = new Array(V); for(u = 0; u { rGraph[u] = nové pole(V); for(v = 0; v rGraph[u][v] = graf[u][v]; } // Toto pole je vyplnené BFS a na uloženie cesty nech parent = new Array(V) // Na začiatku nie je žiadny tok nech max_flow = 0 // Rozšíri tok, kým // existuje cesta od zdroja k potope while (bfs(rGraph, s, t); , parent)) { // Nájdite minimálnu zvyškovú kapacitu hrán // pozdĺž cesty vyplnenej BFS Alebo môžeme povedať // nájsť maximálny prietok cez nájdenú cestu nech cesta_tok = Číslo.MAX_HODNOTA pre (v = t ; v != s; v = rodič[v]) { u = tok_cesty = Math.min(cesta_tok, rGraf[u][v] } // Aktualizácia zvyškových kapacít hrán a //); obrátene hrany pozdĺž cesty for(v = t; v != s; v = rodič[v]) { u = rodič[v]] -= tok_cesty[v][u] + = path_flow } // Pridanie toku cesty k celkovému toku max_flow += cesta_tok } // Návrat celkového toku max_flow } // Kód ovládača // Vytvorme graf zobrazený v príklade vyššie nech graf = [ [ 0 , 16, 13, 0, 0, 0 ], [ 0, 0, 10, 12, 0, 0 ], [ 0, 4, 0, 0, 14, 0 ], [ 0, 0, 9, 0, 0 20], [0, 0, 0, 7, 0, 4], [0, 0, 0, 0, 0, 0]]; document.write('Maximálny možný tok je ' + fordFulkerson(graf, 0, 5)); // Tento kód prispel avanitrachhadiya2155>

Výkon

The maximum possible flow is 23 

Časová zložitosť: O(|V| * E^2) ,kde E je počet hrán a V je počet vrcholov.

Priestorová zložitosť :O(V), ako sme vytvorili front.

Vyššie uvedená implementácia Ford Fulkerson Algorithm je tzv Edmondsov-Karpov algoritmus . Myšlienkou Edmonds-Karp je použiť BFS v implementácii Ford Fulkerson, pretože BFS vždy vyberie cestu s minimálnym počtom hrán. Keď sa použije BFS, časová zložitosť v najhoršom prípade sa môže znížiť na O(VE ² ). Vyššie uvedená implementácia používa reprezentáciu matice susednosti, hoci BFS berie O(V ² ) čas, časová náročnosť vyššie uvedenej implementácie je O(EV ³ ) (Odkaz kniha CLRS na dôkaz časovej náročnosti)

Toto je dôležitý problém, ktorý vzniká v mnohých praktických situáciách. Príklady zahŕňajú maximalizáciu prepravy s danými prevádzkovými limitmi, maximalizáciu toku paketov v počítačových sieťach.
Dincov algoritmus pre maximálny prietok.

Cvičenie:
Upravte vyššie uvedenú implementáciu tak, aby bežala v O(VE ² ) čas.