Nájdite najkratšiu bezpečnú cestu na ceste s nášľapnými mínami
Daná obdĺžniková matica mat[][] kde niektoré bunky obsahujú nášľapné míny (označené 0) a ostatné sú bezpečné (označené 1), nájdite dĺžku najkratšej bezpečnej cesty z ktorejkoľvek bunky v prvom stĺpci do ktorejkoľvek bunky v poslednom stĺpci.
- Nášľapné míny nie sú bezpečné a ich štyri susediace bunky (hore dole vľavo vpravo) sú tiež nebezpečné.
- Povolené sú len horizontálne a vertikálne pohyby do susedných bezpečných buniek.
- Ak nie je možné bezpečne dosiahnuť posledný stĺpec, vráťte sa -1.
Príklady:
Vstup:
s[][] = [ [1 0 1 1 1]
[1 1 1 1 1]
[1 1 1 1 1]
[1 1 1 0 1]
[1 1 1 1 0] ]
výstup: 6
Vysvetlenie: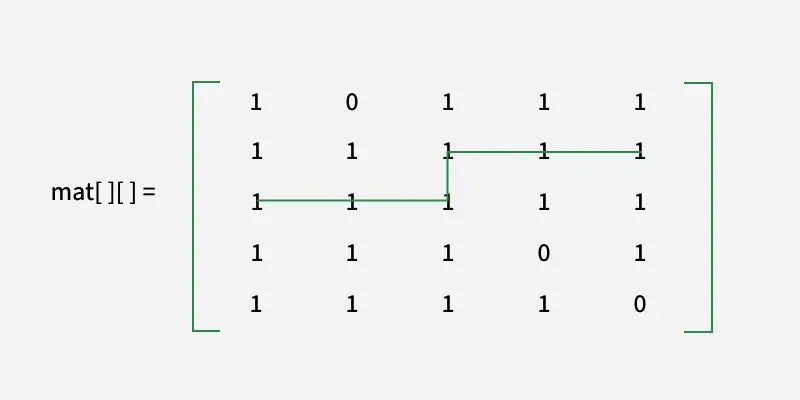
Vidíme, že dĺžka je najkratšia
bezpečná cesta je 6.
Vstup:
s[][] = [ [1 1 1 1 1]
[1 1 0 1 1]
[1 1 1 1 1] ]
výstup: -1
Vysvetlenie: Neexistuje žiadna možná cesta z
od prvého stĺpca po posledný stĺpec.
Obsah
[Prístup] Použitie Backtracking
C++Myšlienka je použiť Backtracking . Najprv označíme všetky susediace bunky nášľapných mín ako nebezpečné. Potom pre každú bezpečnú bunku prvého stĺpca matice postupujeme vpred všetkými povolenými smermi a rekurzívne kontrolujeme, či vedú k cieľu alebo nie. Ak sa nájde cieľ, aktualizujeme hodnotu najkratšej cesty, inak ak nefunguje žiadne z vyššie uvedených riešení, vrátime z našej funkcie hodnotu false.
#include #include #include #include using namespace std ; // Function to mark unsafe cells (landmines and their adjacent cells) void markUnsafeCells ( vector < vector < int >> & mat ) { int r = mat . size (); int c = mat [ 0 ]. size (); // Directions for adjacent cells: up down left right int row [] = { -1 1 0 0 }; int col [] = { 0 0 -1 1 }; vector < vector < int >> temp = mat ; // Mark adjacent cells of landmines (0) as unsafe (0) for ( int i = 0 ; i < r ; i ++ ) { for ( int j = 0 ; j < c ; j ++ ) { if ( temp [ i ][ j ] == 0 ) { for ( int k = 0 ; k < 4 ; k ++ ) { int ni = i + row [ k ]; int nj = j + col [ k ]; if ( ni >= 0 && ni < r && nj >= 0 && nj < c ) { mat [ ni ][ nj ] = 0 ; } } } } } } // DFS to find shortest path from (i j) to any cell in last column int dfs ( vector < vector < int >> & mat vector < vector < bool >> & visited int i int j int c ) { int r = mat . size (); if ( i < 0 || i >= r || j < 0 || j >= c || mat [ i ][ j ] == 0 || visited [ i ][ j ]) { return INT_MAX ; } if ( j == c - 1 ) { return 1 ; } visited [ i ][ j ] = true ; // Four possible moves: up down left right int row [] = { -1 1 0 0 }; int col [] = { 0 0 -1 1 }; int minPath = INT_MAX ; // Try all four directions for ( int k = 0 ; k < 4 ; k ++ ) { int ni = i + row [ k ]; int nj = j + col [ k ]; int pathLength = dfs ( mat visited ni nj c ); if ( pathLength != INT_MAX ) { minPath = min ( minPath 1 + pathLength ); } } // Backtrack - unmark current cell visited [ i ][ j ] = false ; return minPath ; } int findShortestPath ( vector < vector < int >> & mat ) { int r = mat . size (); int c = mat [ 0 ]. size (); // Mark all adjacent cells of landmines as unsafe markUnsafeCells ( mat ); // Initialize visited array vector < vector < bool >> visited ( r vector < bool > ( c false )); int minPath = INT_MAX ; // Try starting from each safe cell in the first column for ( int i = 0 ; i < r ; i ++ ) { if ( mat [ i ][ 0 ] == 1 ) { int pathLength = dfs ( mat visited i 0 c ); if ( pathLength != INT_MAX ) { minPath = min ( minPath pathLength ); } } } return minPath == INT_MAX ? -1 : minPath ; } int main () { vector < vector < int >> mat = { { 1 0 1 1 1 } { 1 1 1 1 1 } { 1 1 1 1 1 } { 1 1 1 0 1 } { 1 1 1 1 0 } }; int result = findShortestPath ( mat ); cout < < result < < endl ; return 0 ; }
Java import java.util.Arrays ; class Solution { // Function to mark unsafe cells (landmines and their adjacent cells) private void markUnsafeCells ( int [][] mat ) { int r = mat . length ; int c = mat [ 0 ] . length ; int [] row = { - 1 1 0 0 }; int [] col = { 0 0 - 1 1 }; // Create a copy to avoid modifying original safe cells prematurely int [][] temp = new int [ r ][ c ] ; for ( int i = 0 ; i < r ; i ++ ) { for ( int j = 0 ; j < c ; j ++ ) { temp [ i ][ j ] = mat [ i ][ j ] ; } } // Mark adjacent cells of landmines (0) as unsafe (0) for ( int i = 0 ; i < r ; i ++ ) { for ( int j = 0 ; j < c ; j ++ ) { if ( temp [ i ][ j ] == 0 ) { for ( int k = 0 ; k < 4 ; k ++ ) { int ni = i + row [ k ] ; int nj = j + col [ k ] ; if ( ni >= 0 && ni < r && nj >= 0 && nj < c ) { mat [ ni ][ nj ] = 0 ; } } } } } } // DFS to find shortest path from (i j) to any cell in last column private int dfs ( int [][] mat boolean [][] visited int i int j int c ) { int r = mat . length ; // If out of bounds blocked or visited if ( i < 0 || i >= r || j < 0 || j >= c || mat [ i ][ j ] == 0 || visited [ i ][ j ] ) { return Integer . MAX_VALUE ; } if ( j == c - 1 ) { return 1 ; } visited [ i ][ j ] = true ; int [] row = { - 1 1 0 0 }; int [] col = { 0 0 - 1 1 }; int minPath = Integer . MAX_VALUE ; // Try all four directions for ( int k = 0 ; k < 4 ; k ++ ) { int ni = i + row [ k ] ; int nj = j + col [ k ] ; int pathLength = dfs ( mat visited ni nj c ); if ( pathLength != Integer . MAX_VALUE ) { minPath = Math . min ( minPath 1 + pathLength ); } } // Backtrack - unmark current cell visited [ i ][ j ] = false ; return minPath ; } public int findShortestPath ( int [][] mat ) { int r = mat . length ; int c = mat [ 0 ] . length ; // Mark all adjacent cells of landmines as unsafe markUnsafeCells ( mat ); boolean [][] visited = new boolean [ r ][ c ] ; int minPath = Integer . MAX_VALUE ; // Try starting from each safe cell in the first column for ( int i = 0 ; i < r ; i ++ ) { if ( mat [ i ][ 0 ] == 1 ) { int pathLength = dfs ( mat visited i 0 c ); if ( pathLength != Integer . MAX_VALUE ) { minPath = Math . min ( minPath pathLength ); } } } return minPath == Integer . MAX_VALUE ? - 1 : minPath ; } public static void main ( String [] args ) { int [][] mat = { { 1 0 1 1 1 } { 1 1 1 1 1 } { 1 1 1 1 1 } { 1 1 1 0 1 } { 1 1 1 1 0 } }; Solution solution = new Solution (); int result = solution . findShortestPath ( mat ); System . out . println ( result ); } }
Python # Function to mark unsafe cells (landmines and their adjacent cells) def mark_unsafe_cells ( mat ): r = len ( mat ) c = len ( mat [ 0 ]) # Directions for adjacent cells: up down left right row = [ - 1 1 0 0 ] col = [ 0 0 - 1 1 ] # Create a copy to avoid modifying original safe cells prematurely temp = [ row [:] for row in mat ] # Mark adjacent cells of landmines (0) as unsafe (0) for i in range ( r ): for j in range ( c ): if temp [ i ][ j ] == 0 : for k in range ( 4 ): ni = i + row [ k ] nj = j + col [ k ] if 0 <= ni < r and 0 <= nj < c : mat [ ni ][ nj ] = 0 # DFS to find shortest path from (i j) to any cell in last column def dfs ( mat visited i j c ): r = len ( mat ) # If out of bounds blocked or visited if i < 0 or i >= r or j < 0 or j >= c or mat [ i ][ j ] == 0 or visited [ i ][ j ]: return float ( 'inf' ) if j == c - 1 : return 1 visited [ i ][ j ] = True # Four possible moves: up down left right row = [ - 1 1 0 0 ] col = [ 0 0 - 1 1 ] min_path = float ( 'inf' ) # Try all four directions for k in range ( 4 ): ni = i + row [ k ] nj = j + col [ k ] path_length = dfs ( mat visited ni nj c ) if path_length != float ( 'inf' ): min_path = min ( min_path 1 + path_length ) # Backtrack - unmark current cell visited [ i ][ j ] = False return min_path def findShortestPath ( mat ): r = len ( mat ) c = len ( mat [ 0 ]) # Mark all adjacent cells of landmines as unsafe mark_unsafe_cells ( mat ) visited = [[ False ] * c for _ in range ( r )] min_path = float ( 'inf' ) # Try starting from each safe cell in the first column for i in range ( r ): if mat [ i ][ 0 ] == 1 : path_length = dfs ( mat visited i 0 c ) if path_length != float ( 'inf' ): min_path = min ( min_path path_length ) return - 1 if min_path == float ( 'inf' ) else min_path def main (): mat = [ [ 1 0 1 1 1 ] [ 1 1 1 1 1 ] [ 1 1 1 1 1 ] [ 1 1 1 0 1 ] [ 1 1 1 1 0 ] ] result = findShortestPath ( mat ) print ( result ) if __name__ == '__main__' : main ()
C# using System ; class GFG { // Function to mark unsafe cells (landmines and their adjacent cells) private void MarkUnsafeCells ( int [][] mat ) { int r = mat . Length ; int c = mat [ 0 ]. Length ; // Directions for adjacent cells: up down left right int [] row = { - 1 1 0 0 }; int [] col = { 0 0 - 1 1 }; // Create a copy to avoid modifying original safe cells prematurely int [][] temp = new int [ r ][]; for ( int i = 0 ; i < r ; i ++ ) { temp [ i ] = new int [ c ]; Array . Copy ( mat [ i ] temp [ i ] c ); } // Mark adjacent cells of landmines (0) as unsafe (0) for ( int i = 0 ; i < r ; i ++ ) { for ( int j = 0 ; j < c ; j ++ ) { if ( temp [ i ][ j ] == 0 ) { for ( int k = 0 ; k < 4 ; k ++ ) { int ni = i + row [ k ]; int nj = j + col [ k ]; if ( ni >= 0 && ni < r && nj >= 0 && nj < c ) { mat [ ni ][ nj ] = 0 ; } } } } } } // DFS to find shortest path from (i j) to any cell in last column private int Dfs ( int [][] mat bool [][] visited int i int j int c ) { int r = mat . Length ; // If out of bounds blocked or visited if ( i < 0 || i >= r || j < 0 || j >= c || mat [ i ][ j ] == 0 || visited [ i ][ j ]) { return int . MaxValue ; } if ( j == c - 1 ) { return 1 ; } visited [ i ][ j ] = true ; int [] row = { - 1 1 0 0 }; int [] col = { 0 0 - 1 1 }; int minPath = int . MaxValue ; // Try all four directions for ( int k = 0 ; k < 4 ; k ++ ) { int ni = i + row [ k ]; int nj = j + col [ k ]; int pathLength = Dfs ( mat visited ni nj c ); if ( pathLength != int . MaxValue ) { minPath = Math . Min ( minPath 1 + pathLength ); } } // Backtrack - unmark current cell visited [ i ][ j ] = false ; return minPath ; } public int FindShortestPath ( int [][] mat ) { int r = mat . Length ; int c = mat [ 0 ]. Length ; // Mark all adjacent cells of landmines as unsafe MarkUnsafeCells ( mat ); bool [][] visited = new bool [ r ][]; for ( int i = 0 ; i < r ; i ++ ) { visited [ i ] = new bool [ c ]; } int minPath = int . MaxValue ; // Try starting from each safe cell in the first column for ( int i = 0 ; i < r ; i ++ ) { if ( mat [ i ][ 0 ] == 1 ) { int pathLength = Dfs ( mat visited i 0 c ); if ( pathLength != int . MaxValue ) { minPath = Math . Min ( minPath pathLength ); } } } return minPath == int . MaxValue ? - 1 : minPath ; } static void Main ( string [] args ) { int [][] mat = new int [][] { new int [] { 1 0 1 1 1 } new int [] { 1 1 1 1 1 } new int [] { 1 1 1 1 1 } new int [] { 1 1 1 0 1 } new int [] { 1 1 1 1 0 } }; GFG solution = new GFG (); int result = solution . FindShortestPath ( mat ); Console . WriteLine ( result ); } }
JavaScript function markUnsafeCells ( mat ) { const r = mat . length ; const c = mat [ 0 ]. length ; // Directions for adjacent cells: up down left right const row = [ - 1 1 0 0 ]; const col = [ 0 0 - 1 1 ]; // Create a copy to avoid modifying original safe cells prematurely const temp = mat . map ( row => [... row ]); // Mark adjacent cells of landmines (0) as unsafe (0) for ( let i = 0 ; i < r ; i ++ ) { for ( let j = 0 ; j < c ; j ++ ) { if ( temp [ i ][ j ] === 0 ) { for ( let k = 0 ; k < 4 ; k ++ ) { const ni = i + row [ k ]; const nj = j + col [ k ]; if ( ni >= 0 && ni < r && nj >= 0 && nj < c ) { mat [ ni ][ nj ] = 0 ; } } } } } } function dfs ( mat visited i j c ) { const r = mat . length ; // If out of bounds blocked or visited if ( i < 0 || i >= r || j < 0 || j >= c || mat [ i ][ j ] === 0 || visited [ i ][ j ]) { return Infinity ; } // If reached the last column if ( j === c - 1 ) { return 1 ; } visited [ i ][ j ] = true ; const row = [ - 1 1 0 0 ]; const col = [ 0 0 - 1 1 ]; let minPath = Infinity ; // Try all four directions for ( let k = 0 ; k < 4 ; k ++ ) { const ni = i + row [ k ]; const nj = j + col [ k ]; const pathLength = dfs ( mat visited ni nj c ); if ( pathLength !== Infinity ) { minPath = Math . min ( minPath 1 + pathLength ); } } // Backtrack - unmark current cell visited [ i ][ j ] = false ; return minPath ; } function findShortestPath ( mat ) { const r = mat . length ; const c = mat [ 0 ]. length ; // Mark all adjacent cells of landmines as unsafe markUnsafeCells ( mat ); const visited = Array ( r ). fill (). map (() => Array ( c ). fill ( false )); let minPath = Infinity ; // Try starting from each safe cell in the first column for ( let i = 0 ; i < r ; i ++ ) { if ( mat [ i ][ 0 ] === 1 ) { const pathLength = dfs ( mat visited i 0 c ); if ( pathLength !== Infinity ) { minPath = Math . min ( minPath pathLength ); } } } return minPath === Infinity ? - 1 : minPath ; } const mat = [ [ 1 0 1 1 1 ] [ 1 1 1 1 1 ] [ 1 1 1 1 1 ] [ 1 1 1 0 1 ] [ 1 1 1 1 0 ] ]; const result = findShortestPath ( mat ); console . log ( result );
Výstup
6
Časová zložitosť: O(4^(r * c)), kde r je počet riadkov a c je počet stĺpcov v danej matici.
Pomocný priestor: O(r * c) pretože používame priestor navyše ako visted[r][c].
[Optimalizovaný prístup] Používanie vyhľadávania na prvom mieste
C++Dá sa vyriešiť v polynomiálnom čase pomocou Breadth-First Search. Všetky bezpečné bunky z posledného stĺpca zaraďte do frontu so vzdialenosťou = 1. Pri postupe BFS sa vypočíta najkratšia cesta ku každej bunke z posledného stĺpca. Nakoniec zo všetkých dosiahnuteľných buniek v prvom stĺpci uveďte minimálnu vzdialenosť.
#include #include #include #include #include #include using namespace std ; int rowNum [ 4 ] = { -1 0 0 1 }; int colNum [ 4 ] = { 0 -1 1 0 }; int findShortestPath ( vector < vector < int >> & mat ) { int n = mat . size (); int m = mat [ 0 ]. size (); queue < array < int 3 >> q ; // Queue to perform BFS int d [ n ][ m ]; for ( int i = 0 ; i < n ; i ++ ) for ( int j = 0 ; j < m ; j ++ ) d [ i ][ j ] = 1e9 ; // Lambda function to check if cell is valid auto isValid = [ & ]( int i int j ) { if ( i < 0 || i >= n || j < 0 || j >= m ) return false ; return true ; }; // Lambda function to check if cell and its adjacent cells are safe auto check = [ & ]( int i int j ) { if ( ! isValid ( i j )) return false ; for ( int k = 0 ; k < 4 ; k ++ ) { if ( isValid ( i + rowNum [ k ] j + colNum [ k ]) && ! mat [ i + rowNum [ k ]][ j + colNum [ k ]]) return false ; } return true ; }; // Pushing cells from the rightmost column into the queue for ( int i = 0 ; i < n ; i ++ ) { if ( check ( i m - 1 )) { q . push ({ i m - 1 1 }); } } // BFS traversal while ( ! q . empty ()) { auto z = q . front (); int x = z [ 0 ] y = z [ 1 ] dis = z [ 2 ]; q . pop (); if ( d [ x ][ y ] > dis ) { d [ x ][ y ] = dis ; for ( int k = 0 ; k < 4 ; k ++ ) { if ( check ( x + rowNum [ k ] y + colNum [ k ])) { q . push ({ x + rowNum [ k ] y + colNum [ k ] dis + 1 }); } } } } // Finding the minimum distance in the first column int ans = 1e9 ; for ( int i = 0 ; i < n ; i ++ ) ans = min ( ans d [ i ][ 0 ]); // If no safe path found return -1 if ( ans >= 1e9 ) ans = -1 ; return ans ; } int main () { vector < vector < int >> mat = { { 1 0 1 1 1 } { 1 1 1 1 1 } { 1 1 1 1 1 } { 1 1 1 0 1 } { 1 1 1 1 0 } }; int result = findShortestPath ( mat ); cout < < result < < endl ; return 0 ; }
Java import java.util.* ; public class Solution { static int [] rowNum = { - 1 0 0 1 }; static int [] colNum = { 0 - 1 1 0 }; public static int findShortestPath ( int [][] mat ) { int n = mat . length ; int m = mat [ 0 ] . length ; Queue < int []> q = new LinkedList <> (); int [][] d = new int [ n ][ m ] ; // Initializing distance array with large values for ( int i = 0 ; i < n ; i ++ ) { Arrays . fill ( d [ i ] ( int ) 1e9 ); } // Lambda-like helper function: check if cell is valid java . util . function . BiFunction < Integer Integer Boolean > isValid = ( i j ) -> { return ! ( i < 0 || i >= n || j < 0 || j >= m ); }; // Helper function: check if cell and adjacent cells are safe java . util . function . BiFunction < Integer Integer Boolean > check = ( i j ) -> { if ( ! isValid . apply ( i j )) return false ; for ( int k = 0 ; k < 4 ; k ++ ) { int ni = i + rowNum [ k ] ; int nj = j + colNum [ k ] ; if ( isValid . apply ( ni nj ) && mat [ ni ][ nj ] == 0 ) return false ; } return true ; }; // Pushing cells from the rightmost column into the queue for ( int i = 0 ; i < n ; i ++ ) { if ( check . apply ( i m - 1 )) { q . add ( new int [] { i m - 1 1 }); } } // BFS traversal while ( ! q . isEmpty ()) { int [] z = q . poll (); int x = z [ 0 ] y = z [ 1 ] dis = z [ 2 ] ; if ( d [ x ][ y ] > dis ) { d [ x ][ y ] = dis ; for ( int k = 0 ; k < 4 ; k ++ ) { int ni = x + rowNum [ k ] ; int nj = y + colNum [ k ] ; if ( check . apply ( ni nj )) { q . add ( new int [] { ni nj dis + 1 }); } } } } // Finding the minimum distance in the first column int ans = ( int ) 1e9 ; for ( int i = 0 ; i < n ; i ++ ) { ans = Math . min ( ans d [ i ][ 0 ] ); } // If no safe path found return -1 if ( ans >= 1e9 ) ans = - 1 ; return ans ; } public static void main ( String [] args ) { int [][] mat = { { 1 0 1 1 1 } { 1 1 1 1 1 } { 1 1 1 1 1 } { 1 1 1 0 1 } { 1 1 1 1 0 } }; int result = findShortestPath ( mat ); System . out . println ( result ); } }
Python from collections import deque rowNum = [ - 1 0 0 1 ] colNum = [ 0 - 1 1 0 ] def findShortestPath ( mat ): n = len ( mat ) m = len ( mat [ 0 ]) q = deque () d = [[ 10 ** 9 for _ in range ( m )] for _ in range ( n )] # Check if cell is valid def isValid ( i j ): return not ( i < 0 or i >= n or j < 0 or j >= m ) # Check if cell and its adjacent cells are safe def check ( i j ): if not isValid ( i j ): return False for k in range ( 4 ): ni nj = i + rowNum [ k ] j + colNum [ k ] if isValid ( ni nj ) and mat [ ni ][ nj ] == 0 : return False return True # Pushing cells from the rightmost column into the queue for i in range ( n ): if check ( i m - 1 ): q . append (( i m - 1 1 )) # BFS traversal while q : x y dis = q . popleft () if d [ x ][ y ] > dis : d [ x ][ y ] = dis for k in range ( 4 ): ni nj = x + rowNum [ k ] y + colNum [ k ] if check ( ni nj ): q . append (( ni nj dis + 1 )) # Finding the minimum distance in the first column ans = min ( d [ i ][ 0 ] for i in range ( n )) # If no safe path found return -1 if ans >= 10 ** 9 : ans = - 1 return ans if __name__ == '__main__' : mat = [ [ 1 0 1 1 1 ] [ 1 1 1 1 1 ] [ 1 1 1 1 1 ] [ 1 1 1 0 1 ] [ 1 1 1 1 0 ] ] result = findShortestPath ( mat ) print ( result )
C# using System ; using System.Collections.Generic ; class Solution { static int [] rowNum = { - 1 0 0 1 }; static int [] colNum = { 0 - 1 1 0 }; // Check if cell is valid static bool IsValid ( int i int j int n int m ) { return ! ( i < 0 || i >= n || j < 0 || j >= m ); } // Check if cell and its adjacent cells are safe static bool Check ( int i int j int [][] mat int n int m ) { if ( ! IsValid ( i j n m )) return false ; for ( int k = 0 ; k < 4 ; k ++ ) { int ni = i + rowNum [ k ]; int nj = j + colNum [ k ]; if ( IsValid ( ni nj n m ) && mat [ ni ][ nj ] == 0 ) return false ; } return true ; } public static int FindShortestPath ( int [][] mat ) { int n = mat . Length ; int m = mat [ 0 ]. Length ; Queue < ( int int int ) > q = new Queue < ( int int int ) > (); int [] d = new int [ n m ]; // Initialize distance array with large value for ( int i = 0 ; i < n ; i ++ ) for ( int j = 0 ; j < m ; j ++ ) d [ i j ] = int . MaxValue / 2 ; // Push safe cells from rightmost column for ( int i = 0 ; i < n ; i ++ ) { if ( Check ( i m - 1 mat n m )) { q . Enqueue (( i m - 1 1 )); } } // BFS traversal while ( q . Count > 0 ) { var ( x y dis ) = q . Dequeue (); if ( d [ x y ] > dis ) { d [ x y ] = dis ; for ( int k = 0 ; k < 4 ; k ++ ) { int ni = x + rowNum [ k ]; int nj = y + colNum [ k ]; if ( Check ( ni nj mat n m )) { q . Enqueue (( ni nj dis + 1 )); } } } } // Find minimum distance in the first column int ans = int . MaxValue / 2 ; for ( int i = 0 ; i < n ; i ++ ) ans = Math . Min ( ans d [ i 0 ]); return ans >= int . MaxValue / 2 ? - 1 : ans ; } static void Main () { int [][] mat = new int [][] { new int [] { 1 0 1 1 1 } new int [] { 1 1 1 1 1 } new int [] { 1 1 1 1 1 } new int [] { 1 1 1 0 1 } new int [] { 1 1 1 1 0 } }; int result = FindShortestPath ( mat ); Console . WriteLine ( result ); } }
JavaScript function findShortestPath ( mat ) { const n = mat . length ; const m = mat [ 0 ]. length ; const rowNum = [ - 1 0 0 1 ]; const colNum = [ 0 - 1 1 0 ]; // Distance matrix initialized to large value const d = Array . from ({ length : n } () => Array ( m ). fill ( Number . MAX_SAFE_INTEGER )); // Check if cell is valid function isValid ( i j ) { return ! ( i < 0 || i >= n || j < 0 || j >= m ); } // Check if cell and its adjacent cells are safe function check ( i j ) { if ( ! isValid ( i j )) return false ; for ( let k = 0 ; k < 4 ; k ++ ) { let ni = i + rowNum [ k ]; let nj = j + colNum [ k ]; if ( isValid ( ni nj ) && mat [ ni ][ nj ] === 0 ) return false ; } return true ; } // Queue for BFS let q = []; // Push safe cells from rightmost column for ( let i = 0 ; i < n ; i ++ ) { if ( check ( i m - 1 )) { q . push ([ i m - 1 1 ]); } } // BFS traversal while ( q . length > 0 ) { let [ x y dis ] = q . shift (); if ( d [ x ][ y ] > dis ) { d [ x ][ y ] = dis ; for ( let k = 0 ; k < 4 ; k ++ ) { let ni = x + rowNum [ k ]; let nj = y + colNum [ k ]; if ( check ( ni nj )) { q . push ([ ni nj dis + 1 ]); } } } } // Find minimum distance in first column let ans = Number . MAX_SAFE_INTEGER ; for ( let i = 0 ; i < n ; i ++ ) { ans = Math . min ( ans d [ i ][ 0 ]); } return ans >= Number . MAX_SAFE_INTEGER ? - 1 : ans ; } const mat = [ [ 1 0 1 1 1 ] [ 1 1 1 1 1 ] [ 1 1 1 1 1 ] [ 1 1 1 0 1 ] [ 1 1 1 1 0 ] ]; const result = findShortestPath ( mat ); console . log ( result );
Výstup
6
Časová zložitosť: O(r * c) kde r a c sú počet riadkov a stĺpcov v danej matici.
Pomocný priestor: O(r * c)