Konverzia z NFA na DFA

NFA môže mať nula, jeden alebo viac ako jeden pohyb z daného stavu na danom vstupnom symbole. NFA môže mať aj NULL ťahy (pohyby bez vstupného symbolu). Na druhej strane, DFA má jeden a len jeden pohyb z daného stavu na danom vstupnom symbole.
Kroky na konverziu NFA na DFA:
Krok 1: Preveďte daný NFA na jeho ekvivalentnú tabuľku prechodov
Aby sme previedli NFA na ekvivalentnú tabuľku prechodu, musíme uviesť všetky stavy, vstupné symboly a pravidlá prechodu. Pravidlá prechodu sú znázornené vo forme matice, kde riadky predstavujú aktuálny stav, stĺpce predstavujú vstupný symbol a bunky predstavujú nasledujúci stav.
Krok 2: Vytvorte počiatočný stav DFA
Počiatočný stav DFA je množina všetkých možných počiatočných stavov v NFA. Táto sada sa nazýva epsilon uzáver počiatočného stavu NFA. Uzáver epsilon je množina všetkých stavov, ktoré možno dosiahnuť z počiatočného stavu nasledujúcimi prechodmi epsilon (?).
Krok 3: Vytvorte tabuľku prechodu služby DFA
Prechodová tabuľka DFA je podobná prechodovej tabuľke NFA, ale namiesto jednotlivých stavov predstavujú riadky a stĺpce množiny stavov. Pre každý vstupný symbol obsahuje zodpovedajúca bunka v tabuľke prechodu epsilon uzáver množiny stavov získaných podľa pravidiel prechodu v tabuľke prechodov NFA.
Krok 4: Vytvorte konečné stavy DFA
Konečné stavy DFA sú množiny stavov, ktoré obsahujú aspoň jeden konečný stav z NFA.
Krok 5: Zjednodušte DFA
DFA získaný v predchádzajúcich krokoch môže obsahovať nepotrebné stavy a prechody. Na zjednodušenie DFA môžeme použiť nasledujúce techniky:
- Odstrániť nedostupné stavy: Stavy, ktoré sa nedajú dosiahnuť z počiatočného stavu, môžu byť odstránené zo služby DFA.
- Odstrániť mŕtve stavy: Štáty, ktoré nemôžu viesť ku konečnému stavu, môžu byť odstránené zo služby DFA.
- Zlúčiť ekvivalentné stavy: Štáty, ktoré majú rovnaké pravidlá prechodu pre všetky vstupné symboly, možno zlúčiť do jedného stavu.
Krok 6: Opakujte kroky 3-5, kým už nebude možné ďalšie zjednodušenie
Po zjednodušení DFA opakujeme kroky 3 až 5, až kým nebude možné ďalšie zjednodušenie. Výsledná získaná DFA je minimalizovaný ekvivalent DFA k danej NFA.
Príklad: Zvážte nasledujúci NFA znázornený na obrázku 1.

Nasledujú rôzne parametre pre NFA. Q = { q0, q1, q2}? = (a, b) F = { q2}? (Prechodová funkcia NFA)
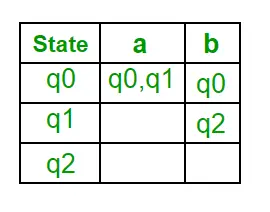
Krok 1: Q' = ? Krok 2: Q' = {q0} Krok 3: Pre každý stav v Q' nájdite stavy pre každý vstupný symbol. V súčasnosti je stav v Q' q0, nájdite pohyby z q0 na vstupnom symbole a a b pomocou prechodovej funkcie NFA a aktualizujte tabuľku prechodov DFA. ?‘ (Prechodová funkcia DFA)

Teraz sa { q0, q1 } bude považovať za jeden stav. Keďže jeho záznam nie je v Q', pridajte ho do Q'. Takže Q' = { q0, { q0, q1 } } Teraz, pohyby zo stavu { q0, q1 } na rôznych vstupných symboloch nie sú prítomné v tabuľke prechodov DFA, vypočítame to takto: ?' ( { q0, q1 } , a) = ? (q0, a) ? ? ( q1, a ) = { q0, q1 } ?‘ ( { q0, q1 }, b ) = ? (q0, b) ? ? ( q1, b ) = { q0, q2 } Teraz aktualizujeme tabuľku prechodov DFA. ?‘ (Prechodová funkcia DFA)

Teraz sa { q0, q2 } bude považovať za jeden stav. Keďže jeho záznam nie je v Q', pridajte ho do Q'. Takže Q' = { q0, { q0, q1 }, { q0, q2 } } Teraz, pohyby zo stavu {q0, q2} na rôznych vstupných symboloch nie sú prítomné v tabuľke prechodov DFA, vypočítame to takto: ?' ( { q0, q2 }, a ) = ? (q0, a) ? ? ( q2, a ) = { q0, q1 } ?‘ ( { q0, q2 }, b ) = ? (q0, b) ? ? ( q2, b ) = { q0 } Teraz aktualizujeme tabuľku prechodu DFA. ?‘ (Prechodová funkcia DFA)
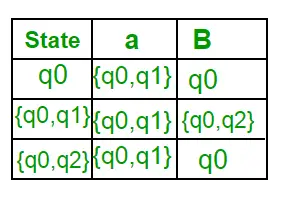
Keďže sa nevygeneruje žiadny nový stav, konverzia je hotová. Konečný stav DFA bude stav, ktorého komponentom je q2, t. j. { q0, q2 } Nasledujú rôzne parametre pre DFA. Q’ = { q0, { q0, q1 }, { q0, q2 } } ? = (a, b) F = { { q0, q2 } } a prechodová funkcia ?‘, ako je uvedené vyššie. Konečná DFA pre vyššie uvedenú NFA je znázornená na obrázku 2.
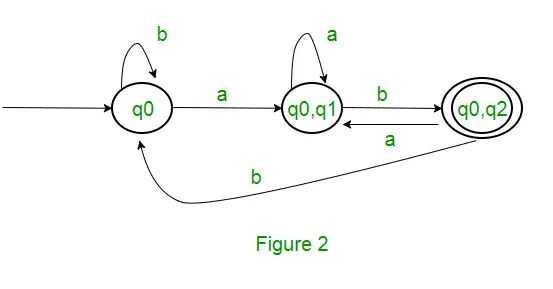
Poznámka : Niekedy nie je jednoduché previesť regulárny výraz na DFA. Najprv môžete previesť regulárny výraz na NFA a potom NFA na DFA.
otázka: Počet stavov v minimálnom deterministickom konečnom automate zodpovedajúcich regulárnemu výrazu (0 + 1)* (10) je ____________.
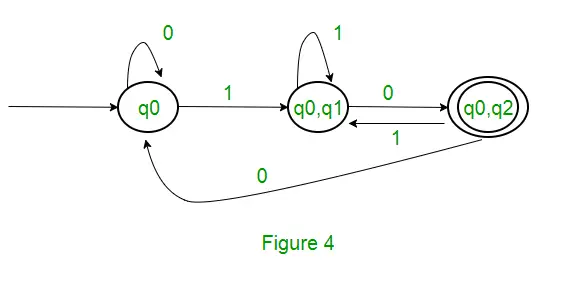
Riešenie : Najprv vytvoríme NFA pre vyššie uvedený výraz. Na vytvorenie NFA pre (0 + 1)* bude NFA v rovnakom stave q0 na vstupnom symbole 0 alebo 1. Potom na zreťazenie pridáme dva ťahy (q0 až q1 pre 1 a q1 až q2 pre 0), ako je znázornené na obrázku 3.
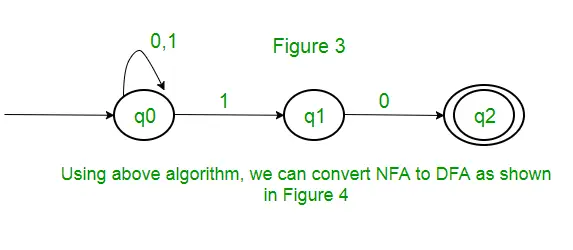
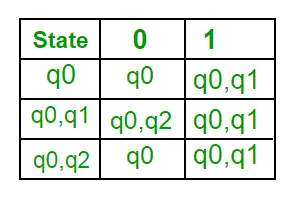
K tomuto článku prispel Sonal Tuteja.