EFEKTÍVNE NAVRHNITE VLOŽKU, ODSTRAŇTE A STREDNE DOTAZY NA SÚPRAVU

Vzhľadom na spočiatku prázdnu sadu a niekoľko dotazov na ňom každé z nasledujúcich typov:

Vložiť - Vložte nový prvok „X“. Vymazať - Odstráňte existujúci prvok „X“. Stredný - Vytlačte stredný prvok čísel, ktoré sú momentálne v množine

Príklad:

Input : Insert 1 Insert 4 Insert 7 Median Output : The first three queries should insert 1 4 and 7 into an empty set. The fourth query should return 4 (median of 1 4 7).

Zastaveného účelu predpokladáme nasledujúce, ale tieto predpoklady nie sú obmedzeniami tu diskutovanej metódy:
1. V každom prípade sú všetky prvky odlišné, čo sa nevyskytuje viac ako raz.
2. „Medián“ dotazu sa uskutočňuje iba vtedy, keď je v sade nepárny počet prvkov. (V prípade rovnomerných čísel budeme musieť urobiť dva dotazy na našom strome segmentu)
3. Prvky v rozsahu sada od 1 do +10^6.

Metóda 1 (naivná)
Pri naivnej implementácii môžeme urobiť prvé dva dotazy v O (1), ale posledný dotaz v O (max_elem), kde max_elem je maximálnym prvkom všetkých čias (vrátane odstránených prvkov).

Predpokladajme pole počítať [] (s veľkosťou 10^6 + 1) na udržanie počtu každého prvku v podskupine. Nasledujúce sú jednoduché a samoliečené algoritmy pre 3 dotazy:
Vložte dotaz X:

 count[x]++; if (x > max_elem) max_elem = x; n++;

Odstrániť X dotaz:

 if (count[x] > 0) count[x]--; n--;

Stredný dotaz:

 sum = 0; i = 0; while( sum  <= n / 2 ) { i++; sum += count[i]; } median = i; return median;

Ilustrácia počtu polí [] predstavujúce množinu {1 4 7 8 9} Medián prvku je „7“:

Efektívne navrhnite vložte deletu a stredné dotazy na súpravu

„Medián“ dotazu má v úmysle nájsť (n + 1)/2 „1“ v poli v tomto prípade 3. „1“; Teraz robíme to isté pomocou segmentového stromu.

Metóda 2 (pomocou Strom )
Robíme a strom Na ukladanie súčtu intervalov, kde interval [A B] predstavuje počet prvkov prítomných v sade, ktorá je v súčasnosti v rozsahu [A B]. Napríklad, ak zvážime vyššie uvedený príklad dotazu (3 7), vráti 2 dotaz (4 4) vráti 1 dotaz (5 5) návraty 0.

Vložte a odstráňte dotazy sú jednoduché a obe sa dajú implementovať pomocou aktualizácie funkcie (int x int diff) (pridáva „dif“ v indexe „x“)

Algoritmus

// adds ‘diff’ at index ‘x’   update(node a b x diff)   // If leaf node If a == b and a == x segmentTree[node] += diff // If non-leaf node and x lies in its range If x is in [a b] // Update children recursively update(2*node a (a + b)/2 x diff) update(2*node + 1 (a + b)/2 + 1 b x diff) // Update node segmentTree[node] = segmentTree[2 * node] + segmentTree[2 * node + 1]

Vyššie uvedená rekurzívna funkcia spustí O (log (max_elem)) (V tomto prípade je max_elem 10^6) a používa sa na vloženie a vymazanie nasledujúcimi hovormi:

Vložte „X“ sa vykonáva pomocou aktualizácie (1 0 10^6 x 1). Všimnite si, že koreň stromu sa odovzdáva index štartu, ktorý sa odovzdáva ako 0 a koncový index ako 10^6, takže všetky rozsahy, ktoré majú X, sú aktualizované.
Odstrániť „X“ sa vykonáva pomocou aktualizácie (1 0 10^6 x -1). Všimnite si, že koreň stromu sa odovzdáva index štartu, ktorý sa odovzdáva ako 0 a koncový index ako 10^6, takže všetky rozsahy, ktoré majú X, sú aktualizované.

Teraz funkcia na nájdenie indexu s KTH „1“, kde „k“ v tomto prípade bude vždy (n + 1) / 2 Toto bude fungovať podobne ako binárne vyhľadávanie, môžete si ho myslieť ako na rekurzívnu funkciu binárneho vyhľadávania na strome segmentu.

Urobme príklad, aby sme pochopili, že náš set má v súčasnosti prvky {1 4 7 8 9}, a preto je reprezentovaný nasledujúcim stromom segmentu.

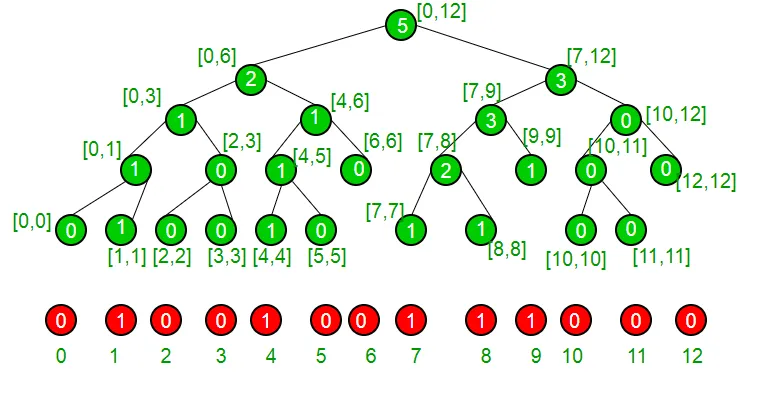
Ak sme v uzle bez listov, sme si istí, že má obidve deti, uvidíme, či má ľavé dieťa viac alebo rovnaké číslo ako „k“, ak áno, sme si istí, že náš index leží v ľavom podstromi, ak má ľavica podstroma menší počet 1 ako k, potom sme si istí, že náš index leží v pravom podsube. Robíme to rekurzívne, aby sme dosiahli náš index a odtiaľ ho vraciame.

Algoritmus

1.findKth(node a b k) 2. If a != b 3. If segmentTree[ 2 * node ] >= k 4. return findKth(2*node a (a + b)/2 k) 5. else 6. return findKth(2*node + 1 (a + b)/2 + 1 b k - segmentTree[ 2 * node ]) 7. else 8. return a

Vyššie uvedená rekurzívna funkcia spustí O (log (max_elem)) .

C++

    // A C++ program to implement insert delete and    // median queries using segment tree    #include          #define maxn 3000005    #define max_elem 1000000    using     namespace     std  ;          // A global array to store segment tree.    // Note: Since it is global all elements are 0.    int     segmentTree  [  maxn  ];          // Update 'node' and its children in segment tree.    // Here 'node' is index in segmentTree[] 'a' and    // 'b' are starting and ending indexes of range stored    // in current node.    // 'diff' is the value to be added to value 'x'.    void     update  (  int     node       int     a       int     b       int     x       int     diff  )      {         // If current node is a leaf node       if     (  a     ==     b     &&     a     ==     x     )         {         // add 'diff' and return       segmentTree  [  node  ]     +=     diff  ;         return     ;         }             // If current node is non-leaf and 'x' is in its       // range       if     (  x     >=     a     &&     x      <=     b  )         {         // update both sub-trees left and right       update  (  node  *  2       a       (  a     +     b  )  /  2       x       diff  );         update  (  node  *  2     +     1       (  a     +     b  )  /  2     +     1       b       x       diff  );             // Finally update current node       segmentTree  [  node  ]     =     segmentTree  [  node  *  2  ]     +         segmentTree  [  node  *  2     +     1  ];         }      }          // Returns k'th node in segment tree    int     findKth  (  int     node       int     a       int     b       int     k  )      {         // non-leaf node will definitely have both       // children; left and right       if     (  a     !=     b  )         {         // If kth element lies in the left subtree       if     (  segmentTree  [  node  *  2  ]     >=     k  )         return     findKth  (  node  *  2       a       (  a     +     b  )  /  2       k  );             // If kth one lies in the right subtree       return     findKth  (  node  *  2     +     1       (  a     +     b  )  /  2     +     1           b       k     -     segmentTree  [  node  *  2  ]);         }             // if at a leaf node return the index it stores       // information about       return     (  segmentTree  [  node  ])  ?     a     :     -1  ;      }          // insert x in the set    void     insert  (  int     x  )      {         update  (  1       0       max_elem       x       1  );      }          // delete x from the set    void     delete  (  int     x  )      {         update  (  1       0       max_elem       x       -1  );      }          // returns median element of the set with odd    // cardinality only    int     median  ()      {         int     k     =     (  segmentTree  [  1  ]     +     1  )     /     2  ;         return     findKth  (  1       0       max_elem       k  );      }          // Driver code    int     main  ()      {         insert  (  1  );         insert  (  4  );         insert  (  7  );         cout      < <     'Median for the set {147} = '          < <     median  ()      < <     endl  ;         insert  (  8  );         insert  (  9  );         cout      < <     'Median for the set {14789} = '       < <     median  ()      < <     endl  ;         delete  (  1  );         delete  (  8  );         cout      < <     'Median for the set {479} = '       < <     median  ()      < <     endl  ;         return     0  ;      }

Java

    // A Java program to implement insert delete and    // median queries using segment tree    import     java.io.*  ;   class   GFG  {   public     static     int     maxn     =     3000005  ;   public     static     int     max_elem     =     1000000  ;   // A global array to store segment tree.    // Note: Since it is global all elements are 0.    public     static     int  []     segmentTree     =     new     int  [  maxn  ]  ;   // Update 'node' and its children in segment tree.    // Here 'node' is index in segmentTree[] 'a' and    // 'b' are starting and ending indexes of range stored    // in current node.    // 'diff' is the value to be added to value 'x'.    public     static     void     update  (  int     node       int     a       int     b           int     x       int     diff  )   {          // If current node is a leaf node       if     (  a     ==     b     &&     a     ==     x     )         {             // Add 'diff' and return       segmentTree  [  node  ]     +=     diff  ;         return     ;         }          // If current node is non-leaf and 'x'      // is in its range      if     (  x     >=     a     &&     x      <=     b  )      {          // Update both sub-trees left and right      update  (  node     *     2       a       (  a     +     b  )     /     2       x       diff  );      update  (  node     *     2     +     1       (  a     +     b  )     /     2     +     1        b       x       diff  );             // Finally update current node      segmentTree  [  node  ]     =     segmentTree  [  node     *     2  ]     +      segmentTree  [  node     *     2     +     1  ]  ;      }   }   // Returns k'th node in segment tree    public     static     int     findKth  (  int     node       int     a           int     b       int     k  )   {          // Non-leaf node will definitely have both       // children; left and right      if     (  a     !=     b  )      {          // If kth element lies in the left subtree       if     (  segmentTree  [  node     *     2  ]     >=     k  )      {      return     findKth  (  node     *     2       a       (  a     +     b  )     /     2       k  );      }          // If kth one lies in the right subtree      return     findKth  (  node     *     2     +     1       (  a     +     b  )     /     2     +     1        b       k     -     segmentTree  [  node     *     2  ]  );          }          // If at a leaf node return the index it stores       // information about       return     (  segmentTree  [  node  ]     !=     0  )     ?     a     :     -  1  ;   }   // Insert x in the set   public     static     void     insert  (  int     x  )   {      update  (  1       0       max_elem       x       1  );   }   // Delete x from the set    public     static     void     delete  (  int     x  )      {      update  (  1       0       max_elem       x       -  1  );      }   // Returns median element of the set   // with odd cardinality only    public     static     int     median  ()   {      int     k     =     (  segmentTree  [  1  ]     +     1  )     /     2  ;         return     findKth  (  1       0       max_elem       k  );   }   // Driver code    public     static     void     main  (  String  []     args  )   {      insert  (  1  );         insert  (  4  );         insert  (  7  );      System  .  out  .  println  (  'Median for the set {147} = '     +         median  ());      insert  (  8  );         insert  (  9  );      System  .  out  .  println  (  'Median for the set {14789} = '     +      median  ());      delete  (  1  );         delete  (  8  );         System  .  out  .  println  (  'Median for the set {479} = '     +         median  ());   }   }   // This code is contributed by avanitrachhadiya2155

Python3

    # A Python3 program to implement insert delete and   # median queries using segment tree   maxn   =   3000005   max_elem   =   1000000   # A global array to store segment tree.   # Note: Since it is global all elements are 0.   segmentTree   =   [  0   for   i   in   range  (  maxn  )]   # Update 'node' and its children in segment tree.   # Here 'node' is index in segmentTree[] 'a' and   # 'b' are starting and ending indexes of range stored   # in current node.   # 'diff' is the value to be added to value 'x'.   def   update  (  node     a     b     x     diff  ):   global   segmentTree   # If current node is a leaf node   if   (  a   ==   b   and   a   ==   x   ):   # add 'diff' and return   segmentTree  [  node  ]   +=   diff   return   # If current node is non-leaf and 'x' is in its   # range   if   (  x   >=   a   and   x    <=   b  ):   # update both sub-trees left and right   update  (  node   *   2     a     (  a   +   b  )  //  2     x     diff  )   update  (  node   *   2   +   1     (  a   +   b  )  //  2   +   1     b     x     diff  )   # Finally update current node   segmentTree  [  node  ]   =   segmentTree  [  node   *   2  ]   +   segmentTree  [  node   *   2   +   1  ]   # Returns k'th node in segment tree   def   findKth  (  node     a     b     k  ):   global   segmentTree   # non-leaf node will definitely have both   # children left and right   if   (  a   !=   b  ):   # If kth element lies in the left subtree   if   (  segmentTree  [  node   *   2  ]   >=   k  ):   return   findKth  (  node   *   2     a     (  a   +   b  )  //  2     k  )   # If kth one lies in the right subtree   return   findKth  (  node   *   2   +   1     (  a   +   b  )  //  2   +   1     b     k   -   segmentTree  [  node   *   2  ])   # if at a leaf node return the index it stores   # information about   return   a   if   (  segmentTree  [  node  ])   else   -  1   # insert x in the set   def   insert  (  x  ):   update  (  1     0     max_elem     x     1  )   # delete x from the set   def   delete  (  x  ):   update  (  1     0     max_elem     x     -  1  )   # returns median element of the set with odd   # cardinality only   def   median  ():   k   =   (  segmentTree  [  1  ]   +   1  )   //   2   return   findKth  (  1     0     max_elem     k  )   # Driver code   if   __name__   ==   '__main__'  :   insert  (  1  )   insert  (  4  )   insert  (  7  )   print  (  'Median for the set {147} ='    median  ())   insert  (  8  )   insert  (  9  )   print  (  'Median for the set {14789} ='    median  ())   delete  (  1  )   delete  (  8  )   print  (  'Median for the set {479} ='    median  ())   # This code is contributed by mohit kumar 29

    // A C# program to implement insert delete    // and median queries using segment tree    using     System  ;   class     GFG  {       public     static     int     maxn     =     3000005  ;   public     static     int     max_elem     =     1000000  ;   // A global array to store segment tree.    // Note: Since it is global all elements are 0.   public     static     int  []     segmentTree     =     new     int  [  maxn  ];   // Update 'node' and its children in segment tree.    // Here 'node' is index in segmentTree[] 'a' and    // 'b' are starting and ending indexes of range stored    // in current node.    // 'diff' is the value to be added to value 'x'.    public     static     void     update  (  int     node       int     a           int     b       int     x       int     diff  )   {          // If current node is a leaf node       if     (  a     ==     b     &&     a     ==     x  )      {          // Add 'diff' and return       segmentTree  [  node  ]     +=     diff  ;         return     ;         }          // If current node is non-leaf and 'x'      // is in its range      if     (  x     >=     a     &&     x      <=     b  )      {          // Update both sub-trees left and right      update  (  node     *     2       a       (  a     +     b  )     /     2       x       diff  );      update  (  node     *     2     +     1       (  a     +     b  )     /     2     +     1        b       x       diff  );             // Finally update current node      segmentTree  [  node  ]     =     segmentTree  [  node     *     2  ]     +      segmentTree  [  node     *     2     +     1  ];      }   }   // Returns k'th node in segment tree   public     static     int     findKth  (  int     node       int     a        int     b       int     k  )   {          // Non-leaf node will definitely have both       // children; left and right      if     (  a     !=     b  )      {          // If kth element lies in the left subtree       if     (  segmentTree  [  node     *     2  ]     >=     k  )      {      return     findKth  (  node     *     2       a           (  a     +     b  )     /     2       k  );      }          // If kth one lies in the right subtree      return     findKth  (  node     *     2     +     1       (  a     +     b  )     /     2     +     1        b       k     -     segmentTree  [  node     *     2  ]);      }          // If at a leaf node return the index it      // stores information about       if     (  segmentTree  [  node  ]     !=     0  )      {      return     a  ;      }      else      {      return     -  1  ;      }   }   // Insert x in the set   public     static     void     insert  (  int     x  )   {      update  (  1       0       max_elem       x       1  );   }   // Delete x from the set    public     static     void     delete  (  int     x  )      {      update  (  1       0       max_elem       x       -  1  );      }   // Returns median element of the set   // with odd cardinality only   public     static     int     median  ()   {      int     k     =     (  segmentTree  [  1  ]     +     1  )     /     2  ;      return     findKth  (  1       0       max_elem       k  );   }   // Driver code   static     public     void     Main  ()   {      insert  (  1  );         insert  (  4  );         insert  (  7  );      Console  .  WriteLine  (  'Median for the set {147} = '     +      median  ());      insert  (  8  );         insert  (  9  );      Console  .  WriteLine  (  'Median for the set {14789} = '     +      median  ());      delete  (  1  );         delete  (  8  );         Console  .  WriteLine  (  'Median for the set {479} = '     +      median  ());   }   }   // This code is contributed by rag2127

JavaScript

     <  script  >   // A Javascript program to implement insert delete and   // median queries using segment tree          let     maxn     =     3000005  ;      let     max_elem     =     1000000  ;          // A global array to store segment tree.      // Note: Since it is global all elements are 0.      let     segmentTree     =     new     Array  (  maxn  );      for  (  let     i  =  0  ;  i   <  maxn  ;  i  ++  )      {      segmentTree  [  i  ]  =  0  ;      }   // Update 'node' and its children in segment tree.   // Here 'node' is index in segmentTree[] 'a' and   // 'b' are starting and ending indexes of range stored   // in current node.   // 'diff' is the value to be added to value 'x'.   function     update  (  node    a    b    x    diff  )   {      // If current node is a leaf node      if     (  a     ==     b     &&     a     ==     x     )      {          // Add 'diff' and return      segmentTree  [  node  ]     +=     diff  ;      return     ;      }          // If current node is non-leaf and 'x'      // is in its range      if     (  x     >=     a     &&     x      <=     b  )      {          // Update both sub-trees left and right      update  (  node     *     2       a       Math  .  floor  ((  a     +     b  )     /     2  )     x       diff  );      update  (  node     *     2     +     1       Math  .  floor  ((  a     +     b  )     /     2  )     +     1        b       x       diff  );          // Finally update current node      segmentTree  [  node  ]     =     segmentTree  [  node     *     2  ]     +      segmentTree  [  node     *     2     +     1  ];      }   }   // Returns k'th node in segment tree   function     findKth  (  node    a    b    k  )   {      // Non-leaf node will definitely have both      // children; left and right      if     (  a     !=     b  )      {          // If kth element lies in the left subtree      if     (  segmentTree  [  node     *     2  ]     >=     k  )      {      return     findKth  (  node     *     2       a       Math  .  floor  ((  a     +     b  )     /     2  )     k  );      }          // If kth one lies in the right subtree      return     findKth  (  node     *     2     +     1       Math  .  floor  ((  a     +     b  )     /     2  )     +     1        b       k     -     segmentTree  [  node     *     2  ]);          }          // If at a leaf node return the index it stores      // information about      return     (  segmentTree  [  node  ]     !=     0  )     ?     a     :     -  1  ;   }   // Insert x in the set   function     insert  (  x  )   {      update  (  1       0       max_elem       x       1  );   }   // Delete x from the set   function     delet  (  x  )   {      update  (  1       0       max_elem       x       -  1  );   }   // Returns median element of the set   // with odd cardinality only   function     median  ()   {      let     k     =     (  segmentTree  [  1  ]     +     1  )     /     2  ;      return     findKth  (  1       0       max_elem       k  );       }   // Driver code   insert  (  1  );   insert  (  4  );   insert  (  7  );   document  .  write  (  'Median for the set {147} = '     +      median  ()  +  '  
'  );   insert  (  8  );   insert  (  9  );   document  .  write  (  'Median for the set {14789} = '     +      median  ()  +  '  
'  );   delet  (  1  );   delet  (  8  );   document  .  write  (  'Median for the set {479} = '     +      median  ()  +  '  
'  );       // This code is contributed by unknown2108    <  /script>

Výstup:

Median for the set {147} = 4 Median for the set {14789} = 7 Median for the set {479} = 7

Záver:
Všetky tri dotazy spúšťajú O (log (max_elem)) V tomto prípade sa max_elem = 10^6, takže log (max_elem) sa rovná 20.
Strom segmentu používa O (max_elem) priestor.

Keby tam bol dotaz odstránenia, mohol by sa to urobiť aj slávnym algoritmom tu .