Analiza complexității în timp și spațiu a sortării fuzionarii
The Complexitatea timpului de Merge Sort este O(n log n) în ambele in medie și cele mai rele cazuri . Complexitatea spațială a Sortare îmbinare este Pe) . 
| Aspect | Complexitate |
|---|---|
| Complexitatea timpului | O(n log n) |
| Complexitatea spațială | Pe) |
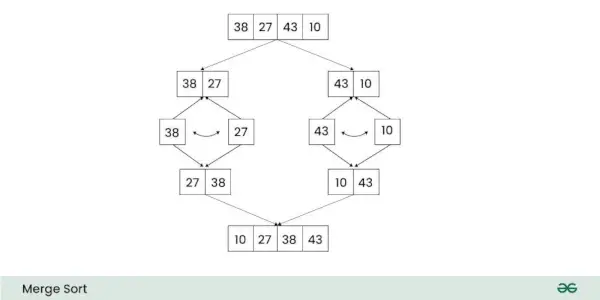
Analiza complexității în timp a sortării prin îmbinare:
Luați în considerare următoarele terminologii:
T(k) = timpul necesar sortării k elemente
M(k) = timpul necesar pentru a îmbina k elemente
Deci, se poate scrie
T(N) = 2 * T(N/2) + M(N)
= 2 * T(N/2) + constantă * N
Aceste elemente N/2 sunt în continuare împărțite în două jumătăți. Asa de,
T(N) = 2 * [2 * T(N/4) + constant * N/2] + constant * N
= 4 * T(N/4) + 2 * N * constantă
. . .
= 2 k * T(N/2 k ) + k * N * constantă
Poate fi împărțit maxim până când rămâne un element. Deci, atunci N/2 k = 1. k = log 2 N
T(N) = N * T(1) + N * log 2 N * constantă
= N + N * log 2 N
Prin urmare, complexitatea timpului este O(N * log 2 N) .
Deci, în cel mai bun caz, în cel mai rău caz și în cazul mediu, complexitatea timpului este aceeași.
Analiza complexității spațiale a sortării de îmbinare:
Sortare îmbinare are o complexitatea spatiului de Pe) . Acest lucru se datorează faptului că folosește o matrice auxiliară de dimensiune n pentru a îmbina jumătățile sortate ale matricei de intrare. Matricea auxiliară este folosită pentru a stoca rezultatul îmbinat, iar matricea de intrare este suprascrisă cu rezultatul sortat.