Timpul necesar pentru a se întâlni în triunghi echilateral
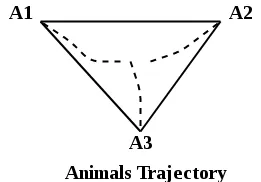
Având în vedere lungimea laturilor triunghiului echilateral (s) și vitezele (v) ale fiecărui animal marcat pe vârfurile triunghiului, aflați timpul după care se întâlnesc dacă încep să se miște spre dreapta lor opusă formând o traiectorie.

Exemple:
Intrare: s = 2 v = 5
Ieșire: 0,266667Intrare: s = 11 v = 556
Ieșire: 0,013189
Abordare:
Pentru a găsi timpul total necesar pentru ca animalele să se întâlnească, luați A împărțit la rata inițială la care două vârfuri se apropie unul de celălalt. Alegeți oricare două vârfuri și se poate observa că primul punct se mișcă în direcția celui de-al doilea cu viteza v, în timp ce al doilea se mișcă în direcția primului (doar luați componenta de-a lungul uneia dintre muchiile triunghiului).
Referinta: StackExchange
Mai jos este implementarea abordării de mai sus:
C++ // CPP code to find time // taken by animals to meet #include using namespace std ; // function to calculate time to meet void timeToMeet ( double s double v ){ double V = 3 * v / 2 ; double time = s / V ; cout < < time ; } // Driver Code int main ( void ) { double s = 25 v = 56 ; timeToMeet ( s v ); return 0 ; }
Java // Java code to find time taken by animals // to meet import java.io.* ; public class GFG { // function to calculate time to meet static void timeToMeet ( double s double v ){ double V = 3 * v / 2 ; double time = s / V ; System . out . println (( float ) time ); } // Driver Code static public void main ( String [] args ) { double s = 25 v = 56 ; timeToMeet ( s v ); } } //This code is contributed by vt_m.
Python3 # Python3 code to find time # taken by animals to meet # function to calculate # time to meet def timeToMeet ( s v ): V = 3 * v / 2 ; time = s / V ; print ( time ); # Driver Code s = 25 ; v = 56 ; timeToMeet ( s v ); # This code is contributed by mits
C# // C# code to find time // taken by animals to meet using System ; public class GFG { // function to calculate time to meet static void timeToMeet ( double s double v ){ double V = 3 * v / 2 ; double time = s / V ; Console . WriteLine (( float ) time ); } // Driver Code static public void Main () { double s = 25 v = 56 ; timeToMeet ( s v ); } } // This code is contributed by vt_m.
PHP // PHP code to find time // taken by animals to meet // function to calculate // time to meet function timeToMeet ( $s $v ) { $V = 3 * $v / 2 ; $time = $s / $V ; echo $time ; } // Driver Code $s = 25 ; $v = 56 ; timeToMeet ( $s $v ); // This code is contributed by anuj_67. ?>
JavaScript < script > // JavaScript code to find time taken by animals // to meet // function to calculate time to meet function timeToMeet ( s v ) { var V = 3 * v / 2 ; var time = s / V ; document . write ( time . toFixed ( 6 )); } // Driver Code var s = 25 v = 56 ; timeToMeet ( s v ); // This code is contributed by todaysgaurav < /script>
Ieșire
0.297619
Complexitatea timpului: O(1)
Spatiu auxiliar: O(1)