Tangente între două poligoane convexe
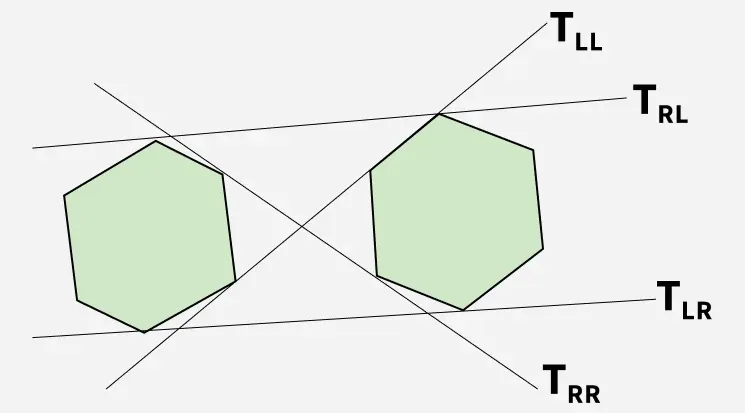
Având în vedere două poligoane convexe, ne propunem să identificăm tangentele inferioare și superioare care le conectează.
După cum se arată în figura de mai jos T RL şi T LR reprezintă tangentele superioare și respectiv inferioare.

Exemple:
Intrare: Primul poligon: [[2 2] [3 3] [5 2] [4 0] [3 1]]
Al doilea poligon: [[-1 0] [0 1] [1 0] [0 -2]].
Ieșire: Tangenta superioară - unirea liniilor (01) și (33)
Tangenta inferioară - linie de unire (0-2) și (40)
Explicaţie: Imaginea arată clar structura și tangentele care leagă cele două poligoane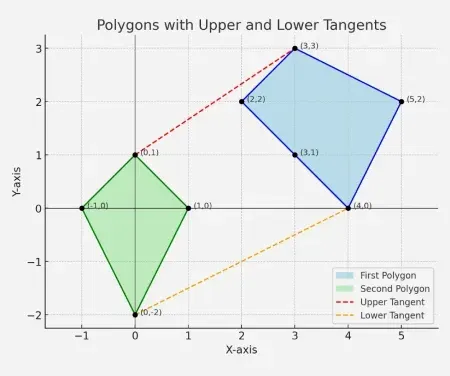
Abordare:
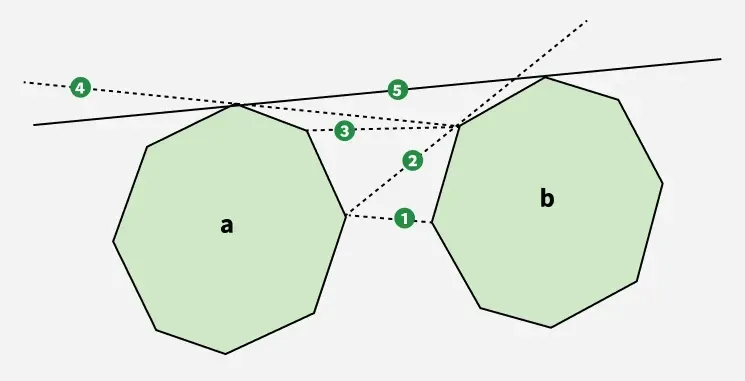
Pentru a găsi tangenta superioară începem prin a selecta două puncte: punctul cel mai din dreapta al poligonului o și punctul cel mai din stânga al poligonului b . Linia care unește aceste două puncte este etichetată ca Linia 1 . Deoarece această linie trece prin poligon b (adică nu este complet deasupra lui) trecem la următorul punct în sens invers acelor de ceasornic pe b formare Linia 2 . Această linie este acum deasupra poligonului b care este bine. Cu toate acestea, traversează poligon o așa că trecem la următorul punct o în sensul acelor de ceasornic creând Linia 3 . Linia 3 traversează încă poligon o determinând o altă mutare către Linia 4 . Linia 4 cu toate acestea traversează poligon b asa ca trecem la Linia 5 . in sfarsit Linia 5 nu traversează niciun poligon, făcându-l tangenta superioară corectă pentru poligoane date.
Pentru a găsi tangentei inferioare, trebuie să ne mișcăm invers prin poligoane, adică dacă linia traversează poligonul b, ne deplasăm în sensul acelor de ceasornic și apoi în sens invers dacă linia traversează poligonul a.
Algoritm pentru tangenta superioara:
L ← linie care unește punctul cel mai din dreapta al lui a și punctul cel mai din stânga al lui b. while (L traversează oricare dintre poligoane) { while(L traversează b) L ← L' : punctul de pe b se deplasează în sus. în timp ce (L încrucișează a) L ← L' : punctul de pe o se mișcă în sus. }
Algoritm pentru tangenta inferioară:
L ← linie care unește punctul cel mai din dreapta al lui a și punctul cel mai din stânga al lui b. while (L traversează oricare dintre poligoane) { while (L traversează b) L ← L' : punctul de pe b se deplasează în jos. în timp ce (L încrucișează a) L ← L' : punctul de pe a se deplasează în jos. }
Rețineți că codul de mai sus calculează doar tangenta superioară. O abordare similară poate fi folosită și pentru a găsi tangentei inferioare.
CPP #include using namespace std ; // Determines the quadrant of a point relative to origin int quad ( vector < int > p ) { if ( p [ 0 ] >= 0 && p [ 1 ] >= 0 ) return 1 ; if ( p [ 0 ] <= 0 && p [ 1 ] >= 0 ) return 2 ; if ( p [ 0 ] <= 0 && p [ 1 ] <= 0 ) return 3 ; return 4 ; } // Returns the orientation of ordered triplet (a b c) // 0 -> Collinear 1 -> Clockwise -1 -> Counterclockwise int orientation ( vector < int > a vector < int > b vector < int > c ) { int res = ( b [ 1 ] - a [ 1 ]) * ( c [ 0 ] - b [ 0 ]) - ( c [ 1 ] - b [ 1 ]) * ( b [ 0 ] - a [ 0 ]); if ( res == 0 ) return 0 ; if ( res > 0 ) return 1 ; return -1 ; } // Compare function to sort points counter-clockwise around center bool compare ( vector < int > p1 vector < int > q1 vector < int > mid ) { vector < int > p = { p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ]}; vector < int > q = { q1 [ 0 ] - mid [ 0 ] q1 [ 1 ] - mid [ 1 ]}; int one = quad ( p ); int two = quad ( q ); if ( one != two ) return ( one < two ); return ( p [ 1 ] * q [ 0 ] < q [ 1 ] * p [ 0 ]); } // Sorts the polygon points counter-clockwise vector < vector < int >> sortPoints ( vector < vector < int >> polygon ) { vector < int > mid = { 0 0 }; int n = polygon . size (); // Calculate center (centroid) of the polygon for ( int i = 0 ; i < n ; i ++ ) { mid [ 0 ] += polygon [ i ][ 0 ]; mid [ 1 ] += polygon [ i ][ 1 ]; polygon [ i ][ 0 ] *= n ; polygon [ i ][ 1 ] *= n ; } // Sort points based on their angle from the center sort ( polygon . begin () polygon . end () [ mid ]( vector < int > p1 vector < int > p2 ) { return compare ( p1 p2 mid ); }); // Divide back to original coordinates for ( int i = 0 ; i < n ; i ++ ) { polygon [ i ][ 0 ] /= n ; polygon [ i ][ 1 ] /= n ; } return polygon ; } // Finds the upper tangent between two convex polygons a and b // Returns two points forming the upper tangent vector < vector < int >> findUpperTangent ( vector < vector < int >> a vector < vector < int >> b ) { int n1 = a . size () n2 = b . size (); // Find the rightmost point of polygon a and leftmost point of polygon b int maxa = INT_MIN ; for ( auto & p : a ) maxa = max ( maxa p [ 0 ]); int minb = INT_MAX ; for ( auto & p : b ) minb = min ( minb p [ 0 ]); // Sort both polygons counter-clockwise a = sortPoints ( a ); b = sortPoints ( b ); // Ensure polygon a is to the left of polygon b if ( minb < maxa ) swap ( a b ); n1 = a . size (); n2 = b . size (); // Find the rightmost point in a int ia = 0 ib = 0 ; for ( int i = 1 ; i < n1 ; i ++ ) if ( a [ i ][ 0 ] > a [ ia ][ 0 ]) ia = i ; // Find the leftmost point in b for ( int i = 1 ; i < n2 ; i ++ ) if ( b [ i ][ 0 ] < b [ ib ][ 0 ]) ib = i ; // Initialize starting points int inda = ia indb = ib ; bool done = false ; // Find upper tangent using orientation checks while ( ! done ) { done = true ; // Move to next point in a if necessary while ( orientation ( b [ indb ] a [ inda ] a [( inda + 1 ) % n1 ]) > 0 ) inda = ( inda + 1 ) % n1 ; // Move to previous point in b if necessary while ( orientation ( a [ inda ] b [ indb ] b [( n2 + indb - 1 ) % n2 ]) < 0 ) { indb = ( n2 + indb - 1 ) % n2 ; done = false ; } } // Return the points forming the upper tangent return { a [ inda ] b [ indb ]}; } // Main driver code int main () { vector < vector < int >> a = {{ 2 2 } { 3 1 } { 3 3 } { 5 2 } { 4 0 }}; vector < vector < int >> b = {{ 0 1 } { 1 0 } { 0 -2 } { -1 0 }}; vector < vector < int >> tangent = findUpperTangent ( a b ); for ( auto it : tangent ){ cout < < it [ 0 ] < < ' ' < < it [ 1 ] < < ' n ' ; } return 0 ; }
Java import java.util.* ; class GfG { // Determines the quadrant of a point static int quad ( int [] p ) { if ( p [ 0 ] >= 0 && p [ 1 ] >= 0 ) return 1 ; if ( p [ 0 ] <= 0 && p [ 1 ] >= 0 ) return 2 ; if ( p [ 0 ] <= 0 && p [ 1 ] <= 0 ) return 3 ; return 4 ; } // Checks whether the line is crossing the polygon static int orientation ( int [] a int [] b int [] c ) { int res = ( b [ 1 ] - a [ 1 ] ) * ( c [ 0 ] - b [ 0 ] ) - ( c [ 1 ] - b [ 1 ] ) * ( b [ 0 ] - a [ 0 ] ); if ( res == 0 ) return 0 ; if ( res > 0 ) return 1 ; return - 1 ; } // Compare function for sorting static class PointComparator implements Comparator < int []> { int [] mid ; public PointComparator ( int [] mid ) { this . mid = mid ; } public int compare ( int [] p1 int [] p2 ) { int [] p = { p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ] }; int [] q = { p2 [ 0 ] - mid [ 0 ] p2 [ 1 ] - mid [ 1 ] }; int one = quad ( p ); int two = quad ( q ); if ( one != two ) return one - two ; return p [ 1 ] * q [ 0 ] - q [ 1 ] * p [ 0 ] ; } } // Finds upper tangent of two polygons 'a' and 'b' // represented as 2D arrays and stores the result static int [][] findUpperTangent ( int [][] a int [][] b ) { // n1 -> number of points in polygon a // n2 -> number of points in polygon b int n1 = a . length n2 = b . length ; int [] mid = { 0 0 }; int maxa = Integer . MIN_VALUE ; // Calculate centroid for polygon a and adjust points for scaling for ( int i = 0 ; i < n1 ; i ++ ) { maxa = Math . max ( maxa a [ i ][ 0 ] ); mid [ 0 ] += a [ i ][ 0 ] ; mid [ 1 ] += a [ i ][ 1 ] ; a [ i ][ 0 ] *= n1 ; a [ i ][ 1 ] *= n1 ; } // Sorting the points in counter-clockwise order for polygon a Arrays . sort ( a new PointComparator ( mid )); for ( int i = 0 ; i < n1 ; i ++ ) { a [ i ][ 0 ] /= n1 ; a [ i ][ 1 ] /= n1 ; } mid [ 0 ] = 0 ; mid [ 1 ] = 0 ; int minb = Integer . MAX_VALUE ; // Calculate centroid for polygon b and adjust points for scaling for ( int i = 0 ; i < n2 ; i ++ ) { mid [ 0 ] += b [ i ][ 0 ] ; mid [ 1 ] += b [ i ][ 1 ] ; minb = Math . min ( minb b [ i ][ 0 ] ); b [ i ][ 0 ] *= n2 ; b [ i ][ 1 ] *= n2 ; } // Sorting the points in counter-clockwise order for polygon b Arrays . sort ( b new PointComparator ( mid )); for ( int i = 0 ; i < n2 ; i ++ ) { b [ i ][ 0 ] /= n2 ; b [ i ][ 1 ] /= n2 ; } // If a is to the right of b swap a and b if ( minb < maxa ) { int [][] temp = a ; a = b ; b = temp ; n1 = a . length ; n2 = b . length ; } // ia -> rightmost point of a int ia = 0 ib = 0 ; for ( int i = 1 ; i < n1 ; i ++ ) { if ( a [ i ][ 0 ] > a [ ia ][ 0 ] ) ia = i ; } // ib -> leftmost point of b for ( int i = 1 ; i < n2 ; i ++ ) { if ( b [ i ][ 0 ] < b [ ib ][ 0 ] ) ib = i ; } // Finding the upper tangent int inda = ia indb = ib ; boolean done = false ; while ( ! done ) { done = true ; while ( orientation ( b [ indb ] a [ inda ] a [ ( inda + 1 ) % n1 ] ) > 0 ) inda = ( inda + 1 ) % n1 ; while ( orientation ( a [ inda ] b [ indb ] b [ ( n2 + indb - 1 ) % n2 ] ) < 0 ) { indb = ( n2 + indb - 1 ) % n2 ; done = false ; } } // Returning the upper tangent as a 2D array return new int [][] { { a [ inda ][ 0 ] a [ inda ][ 1 ] } { b [ indb ][ 0 ] b [ indb ][ 1 ] } }; } // Driver code public static void main ( String [] args ) { int [][] a = {{ 2 2 }{ 3 1 }{ 3 3 }{ 5 2 }{ 4 0 }}; int [][] b = {{ 0 1 }{ 1 0 }{ 0 - 2 }{ - 1 0 }}; // Get the upper tangent as a 2D array int [][] upperTangent = findUpperTangent ( a b ); // Store or use the result System . out . println ( upperTangent [ 0 ][ 0 ] + ' ' + upperTangent [ 0 ][ 1 ] ); System . out . println ( upperTangent [ 1 ][ 0 ] + ' ' + upperTangent [ 1 ][ 1 ] ); } }
Python from functools import cmp_to_key def quad ( p ): if p [ 0 ] >= 0 and p [ 1 ] >= 0 : return 1 if p [ 0 ] <= 0 and p [ 1 ] >= 0 : return 2 if p [ 0 ] <= 0 and p [ 1 ] <= 0 : return 3 return 4 def orientation ( a b c ): res = ( b [ 1 ] - a [ 1 ]) * ( c [ 0 ] - b [ 0 ]) - ( c [ 1 ] - b [ 1 ]) * ( b [ 0 ] - a [ 0 ]) if res == 0 : return 0 if res > 0 : return 1 return - 1 def compare ( mid ): def cmp ( p1 q1 ): p = [ p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ]] q = [ q1 [ 0 ] - mid [ 0 ] q1 [ 1 ] - mid [ 1 ]] one = quad ( p ) two = quad ( q ) if one != two : return one - two if p [ 1 ] * q [ 0 ] < q [ 1 ] * p [ 0 ]: return - 1 return 1 return cmp def findUpperTangent ( a b ): n1 n2 = len ( a ) len ( b ) mid_a = [ 0 0 ] maxa = float ( '-inf' ) for i in range ( n1 ): maxa = max ( maxa a [ i ][ 0 ]) mid_a [ 0 ] += a [ i ][ 0 ] mid_a [ 1 ] += a [ i ][ 1 ] a = sorted ( a key = cmp_to_key ( compare ( mid_a ))) mid_b = [ 0 0 ] minb = float ( 'inf' ) for i in range ( n2 ): minb = min ( minb b [ i ][ 0 ]) mid_b [ 0 ] += b [ i ][ 0 ] mid_b [ 1 ] += b [ i ][ 1 ] b = sorted ( b key = cmp_to_key ( compare ( mid_b ))) if minb < maxa : a b = b a n1 n2 = n2 n1 ia = 0 for i in range ( 1 n1 ): if a [ i ][ 0 ] > a [ ia ][ 0 ]: ia = i ib = 0 for i in range ( 1 n2 ): if b [ i ][ 0 ] < b [ ib ][ 0 ]: ib = i inda indb = ia ib done = False while not done : done = True while orientation ( b [ indb ] a [ inda ] a [( inda + 1 ) % n1 ]) > 0 : inda = ( inda + 1 ) % n1 while orientation ( a [ inda ] b [ indb ] b [( n2 + indb - 1 ) % n2 ]) < 0 : indb = ( n2 + indb - 1 ) % n2 done = False # return integer coordinates return [[ int ( a [ inda ][ 0 ]) int ( a [ inda ][ 1 ])] [ int ( b [ indb ][ 0 ]) int ( b [ indb ][ 1 ])]] # Driver Code if __name__ == '__main__' : a = [ [ 2 2 ] [ 3 1 ] [ 3 3 ] [ 5 2 ] [ 4 0 ] ] b = [ [ 0 1 ] [ 1 0 ] [ 0 - 2 ] [ - 1 0 ] ] upperTangent = findUpperTangent ( a b ) for point in upperTangent : print ( f ' { point [ 0 ] } { point [ 1 ] } ' )
C# using System ; public class UpperTangentFinder { static int Quad ( int x int y ) { if ( x >= 0 && y >= 0 ) return 1 ; if ( x <= 0 && y >= 0 ) return 2 ; if ( x <= 0 && y <= 0 ) return 3 ; return 4 ; } static int Orientation ( int [] a int [] b int [] c ) { int res = ( b [ 1 ] - a [ 1 ]) * ( c [ 0 ] - b [ 0 ]) - ( c [ 1 ] - b [ 1 ]) * ( b [ 0 ] - a [ 0 ]); if ( res == 0 ) return 0 ; return res > 0 ? 1 : - 1 ; } static bool Compare ( int [] p1 int [] p2 int [] mid ) { int [] p = { p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ] }; int [] q = { p2 [ 0 ] - mid [ 0 ] p2 [ 1 ] - mid [ 1 ] }; int quadP = Quad ( p [ 0 ] p [ 1 ]); int quadQ = Quad ( q [ 0 ] q [ 1 ]); if ( quadP != quadQ ) return quadP < quadQ ; return ( p [ 1 ] * q [ 0 ]) < ( q [ 1 ] * p [ 0 ]); } static int [] SortPoints ( int [] polygon ) { int n = polygon . GetLength ( 0 ); int [] mid = { 0 0 }; for ( int i = 0 ; i < n ; i ++ ) { mid [ 0 ] += polygon [ i 0 ]; mid [ 1 ] += polygon [ i 1 ]; polygon [ i 0 ] *= n ; polygon [ i 1 ] *= n ; } for ( int i = 0 ; i < n - 1 ; i ++ ) { for ( int j = i + 1 ; j < n ; j ++ ) { int [] p1 = { polygon [ i 0 ] polygon [ i 1 ] }; int [] p2 = { polygon [ j 0 ] polygon [ j 1 ] }; if ( ! Compare ( p1 p2 mid )) { int tempX = polygon [ i 0 ] tempY = polygon [ i 1 ]; polygon [ i 0 ] = polygon [ j 0 ]; polygon [ i 1 ] = polygon [ j 1 ]; polygon [ j 0 ] = tempX ; polygon [ j 1 ] = tempY ; } } } for ( int i = 0 ; i < n ; i ++ ) { polygon [ i 0 ] /= n ; polygon [ i 1 ] /= n ; } return polygon ; } static int [] FindUpperTangent ( int [] a int [] b ) { int n1 = a . GetLength ( 0 ); int n2 = b . GetLength ( 0 ); int maxa = int . MinValue ; for ( int i = 0 ; i < n1 ; i ++ ) maxa = Math . Max ( maxa a [ i 0 ]); int minb = int . MaxValue ; for ( int i = 0 ; i < n2 ; i ++ ) minb = Math . Min ( minb b [ i 0 ]); a = SortPoints ( a ); b = SortPoints ( b ); if ( minb < maxa ) { int [] temp = a ; a = b ; b = temp ; n1 = a . GetLength ( 0 ); n2 = b . GetLength ( 0 ); } int ia = 0 ib = 0 ; for ( int i = 1 ; i < n1 ; i ++ ) if ( a [ i 0 ] > a [ ia 0 ]) ia = i ; for ( int i = 1 ; i < n2 ; i ++ ) if ( b [ i 0 ] < b [ ib 0 ]) ib = i ; int inda = ia indb = ib ; bool done = false ; while ( ! done ) { done = true ; while ( Orientation ( new int [] { b [ indb 0 ] b [ indb 1 ] } new int [] { a [ inda 0 ] a [ inda 1 ] } new int [] { a [( inda + 1 ) % n1 0 ] a [( inda + 1 ) % n1 1 ] }) > 0 ){ inda = ( inda + 1 ) % n1 ; } while ( Orientation ( new int [] { a [ inda 0 ] a [ inda 1 ] } new int [] { b [ indb 0 ] b [ indb 1 ] } new int [] { b [( n2 + indb - 1 ) % n2 0 ] b [( n2 + indb - 1 ) % n2 1 ] }) < 0 ){ indb = ( n2 + indb - 1 ) % n2 ; done = false ; } } int [] result = new int [ 2 2 ]; result [ 0 0 ] = a [ inda 0 ]; result [ 0 1 ] = a [ inda 1 ]; result [ 1 0 ] = b [ indb 0 ]; result [ 1 1 ] = b [ indb 1 ]; return result ; } public static void Main ( string [] args ) { int [] a = new int [] { { 2 2 } { 3 1 } { 3 3 } { 5 2 } { 4 0 } }; int [] b = new int [] { { 0 1 } { 1 0 } { 0 - 2 } { - 1 0 } }; int [] tangent = FindUpperTangent ( a b ); for ( int i = 0 ; i < 2 ; i ++ ) { Console . WriteLine ( tangent [ i 0 ] + ' ' + tangent [ i 1 ]); } } }
JavaScript // Determine the quadrant of a point function quad ( p ) { if ( p [ 0 ] >= 0 && p [ 1 ] >= 0 ) return 1 ; if ( p [ 0 ] <= 0 && p [ 1 ] >= 0 ) return 2 ; if ( p [ 0 ] <= 0 && p [ 1 ] <= 0 ) return 3 ; return 4 ; } // Find orientation of triplet (a b c) function orientation ( a b c ) { let res = ( b [ 1 ] - a [ 1 ]) * ( c [ 0 ] - b [ 0 ]) - ( c [ 1 ] - b [ 1 ]) * ( b [ 0 ] - a [ 0 ]); if ( res === 0 ) return 0 ; return res > 0 ? 1 : - 1 ; } // Compare two points based on mid function compare ( p1 p2 mid ) { let p = [ p1 [ 0 ] - mid [ 0 ] p1 [ 1 ] - mid [ 1 ]]; let q = [ p2 [ 0 ] - mid [ 0 ] p2 [ 1 ] - mid [ 1 ]]; let quadP = quad ( p ); let quadQ = quad ( q ); if ( quadP !== quadQ ) return quadP - quadQ ; return ( p [ 1 ] * q [ 0 ]) - ( q [ 1 ] * p [ 0 ]); } // Sort polygon points counter-clockwise function sortPoints ( polygon ) { let n = polygon . length ; let mid = [ 0 0 ]; for ( let i = 0 ; i < n ; i ++ ) { mid [ 0 ] += polygon [ i ][ 0 ]; mid [ 1 ] += polygon [ i ][ 1 ]; polygon [ i ][ 0 ] *= n ; polygon [ i ][ 1 ] *= n ; } polygon . sort (( p1 p2 ) => compare ( p1 p2 mid )); for ( let i = 0 ; i < n ; i ++ ) { polygon [ i ][ 0 ] = Math . floor ( polygon [ i ][ 0 ] / n ); polygon [ i ][ 1 ] = Math . floor ( polygon [ i ][ 1 ] / n ); } return polygon ; } // Find upper tangent between two convex polygons function findUpperTangent ( a b ) { let n1 = a . length ; let n2 = b . length ; let maxa = - Infinity ; for ( let i = 0 ; i < n1 ; i ++ ) maxa = Math . max ( maxa a [ i ][ 0 ]); let minb = Infinity ; for ( let i = 0 ; i < n2 ; i ++ ) minb = Math . min ( minb b [ i ][ 0 ]); a = sortPoints ( a ); b = sortPoints ( b ); if ( minb < maxa ) { let temp = a ; a = b ; b = temp ; n1 = a . length ; n2 = b . length ; } let ia = 0 ib = 0 ; for ( let i = 1 ; i < n1 ; i ++ ) if ( a [ i ][ 0 ] > a [ ia ][ 0 ]) ia = i ; for ( let i = 1 ; i < n2 ; i ++ ) if ( b [ i ][ 0 ] < b [ ib ][ 0 ]) ib = i ; let inda = ia indb = ib ; let done = false ; while ( ! done ) { done = true ; while ( orientation ( b [ indb ] a [ inda ] a [( inda + 1 ) % n1 ]) > 0 ) inda = ( inda + 1 ) % n1 ; while ( orientation ( a [ inda ] b [ indb ] b [( n2 + indb - 1 ) % n2 ]) < 0 ) { indb = ( n2 + indb - 1 ) % n2 ; done = false ; } } return [ a [ inda ] b [ indb ]]; } // Driver code let a = [[ 2 2 ][ 3 1 ][ 3 3 ][ 5 2 ][ 4 0 ]]; let b = [[ 0 1 ][ 1 0 ][ 0 - 2 ][ - 1 0 ]]; let tangent = findUpperTangent ( a b ); for ( let point of tangent ) { console . log ( point [ 0 ] + ' ' + point [ 1 ]); }
Ieșire
upper tangent (01) (33)
Complexitatea timpului: O(n1 log (n1) + n2 log(n2))
Spațiu auxiliar: O(1)