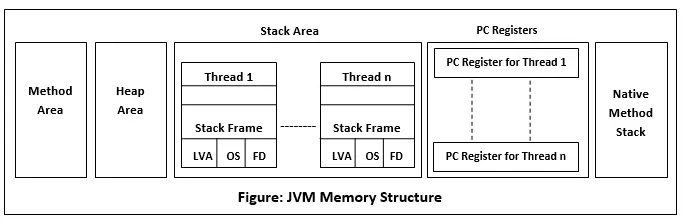
Problem komiwojażera (TSP):

Biorąc pod uwagę zbiór miast i odległość między każdą parą miast, problem polega na znalezieniu najkrótszej możliwej trasy, która odwiedza każde miasto dokładnie raz i wraca do punktu początkowego. Zwróć uwagę na różnicę między cyklem Hamiltona a TSP. Problem cyklu Hamiltona polega na ustaleniu, czy istnieje trasa, która odwiedza każde miasto dokładnie raz. Wiemy, że istnieje trasa Hamiltona (ponieważ wykres jest kompletny) i w rzeczywistości istnieje wiele takich wycieczek, problem polega na znalezieniu minimalnej wagi cyklu Hamiltona.

Rozważmy na przykład wykres pokazany na rysunku po prawej stronie. Trasa TSP na wykresie to 1-2-4-3-1. Koszt wycieczki wynosi 10+25+30+15, czyli 80. Problem jest znanym problemem NP-trudnym. Nie ma rozwiązania tego problemu w czasie wielomianowym. Poniżej przedstawiono różne rozwiązania problemu komiwojażera.

Naiwne rozwiązanie:

1) Rozważ miasto 1 jako punkt początkowy i końcowy.

2) Wygeneruj wszystko (n-1)! Permutacje miast.

3) Oblicz koszt każdej permutacji i śledź permutację o minimalnym koszcie.

4) Zwróć permutację przy minimalnym koszcie.

Złożoność czasowa: ?(n!)

Programowanie dynamiczne:

Niech dany zbiór wierzchołków będzie wynosił {1, 2, 3, 4,….n}. Rozważmy 1 jako punkt początkowy i końcowy wyniku. Dla każdego innego wierzchołka I (innego niż 1) znajdujemy ścieżkę minimalnego kosztu, w której 1 jest punktem początkowym, I punktem końcowym, a wszystkie wierzchołki pojawiają się dokładnie raz. Niech koszt tej ścieżki będzie kosztować (i), a koszt odpowiedniego cyklu będzie kosztować (i) + dist(i, 1) gdzie dist(i, 1) to odległość od I do 1. Na koniec zwracamy minimum wszystkich wartości [cost(i) + dist(i, 1)]. Na razie wygląda to prosto.

Teraz pytanie brzmi: jak uzyskać koszt (i)? Aby obliczyć koszt (i) za pomocą programowania dynamicznego, musimy mieć pewną relację rekurencyjną w zakresie podproblemów.

Zdefiniujmy termin C(S, i) będzie kosztem ścieżki o minimalnym koszcie odwiedzającej każdy wierzchołek zbioru S dokładnie raz, zaczynając od 1 i kończąc na i . Zaczynamy od wszystkich podzbiorów o rozmiarze 2 i obliczamy C(S, i) dla wszystkich podzbiorów, gdzie S jest podzbiorem, następnie obliczamy C(S, i) dla wszystkich podzbiorów S o rozmiarze 3 i tak dalej. Zauważ, że 1 musi być obecne w każdym podzbiorze.

If size of S is 2, then S must be {1, i}, C(S, i) = dist(1, i) Else if size of S is greater than 2. C(S, i) = min { C(S-{i}, j) + dis(j, i)} where j belongs to S, j != i and j != 1. 

Poniżej znajduje się dynamiczne rozwiązanie programistyczne problemu przy użyciu podejścia rekursywnego z góry na dół i zapamiętanego: -

Aby zachować podzbiory, możemy użyć masek bitowych do przedstawienia pozostałych węzłów w naszym podzbiorze. Ponieważ bity działają szybciej, a graf ma tylko kilka węzłów, lepiej jest używać masek bitowych.

Na przykład: -

10100 reprezentuje węzeł 2, a węzeł 4 pozostał w zestawie do przetworzenia

010010 reprezentuje węzeł 1 i 4, które pozostały w podzbiorze.

UWAGA: – zignoruj ​​bit 0, ponieważ nasz wykres jest oparty na 1

C++

#include> using> namespace> std;> // there are four nodes in example graph (graph is 1-based)> const> int> n = 4;> // give appropriate maximum to avoid overflow> const> int> MAX = 1000000;> // dist[i][j] represents shortest distance to go from i to j> // this matrix can be calculated for any given graph using> // all-pair shortest path algorithms> int> dist[n + 1][n + 1] = {> > { 0, 0, 0, 0, 0 }, { 0, 0, 10, 15, 20 },> > { 0, 10, 0, 25, 25 }, { 0, 15, 25, 0, 30 },> > { 0, 20, 25, 30, 0 },> };> // memoization for top down recursion> int> memo[n + 1][1 < < (n + 1)];> int> fun(> int> i,> int> mask)> > > // base case> > // if only ith bit and 1st bit is set in our mask,> > // it implies we have visited all other nodes already> > if> (mask == ((1 < < i)> // Driver program to test above logic> int> main()> {> > int> ans = MAX;> > for> (> int> i = 1; i <= n; i++)> > // try to go from node 1 visiting all nodes in> > // between to i then return from i taking the> > // shortest route to 1> > ans = std::min(ans, fun(i, (1 < < (n + 1)) - 1)> > + dist[i][1]);> > printf> (> 'The cost of most efficient tour = %d'> , ans);> > return> 0;> }> // This code is contributed by Serjeel Ranjan>

Jawa

import> java.io.*;> import> java.util.*;> public> class> TSE {> > // there are four nodes in example graph (graph is> > // 1-based)> > static> int> n => 4> ;> > // give appropriate maximum to avoid overflow> > static> int> MAX => 1000000> ;> > // dist[i][j] represents shortest distance to go from i> > // to j this matrix can be calculated for any given> > // graph using all-pair shortest path algorithms> > static> int> [][] dist = {> > {> 0> ,> 0> ,> 0> ,> 0> ,> 0> }, {> 0> ,> 0> ,> 10> ,> 15> ,> 20> },> > {> 0> ,> 10> ,> 0> ,> 25> ,> 25> }, {> 0> ,> 15> ,> 25> ,> 0> ,> 30> },> > {> 0> ,> 20> ,> 25> ,> 30> ,> 0> },> > };> > // memoization for top down recursion> > static> int> [][] memo => new> int> [n +> 1> ][> 1> < < (n +> 1> )];> > static> int> fun(> int> i,> int> mask)> > > > // base case> > // if only ith bit and 1st bit is set in our mask,> > // it implies we have visited all other nodes> > // already> > if> (mask == ((> 1> < < i)> > // Driver program to test above logic> > public> static> void> main(String[] args)> > {> > int> ans = MAX;> > for> (> int> i => 1> ; i <= n; i++)> > // try to go from node 1 visiting all nodes in> > // between to i then return from i taking the> > // shortest route to 1> > ans = Math.min(ans, fun(i, (> 1> < < (n +> 1> )) -> 1> )> > + dist[i][> 1> ]);> > System.out.println(> > 'The cost of most efficient tour = '> + ans);> > }> }> // This code is contributed by Serjeel Ranjan>

Python3

n> => 4> # there are four nodes in example graph (graph is 1-based)> # dist[i][j] represents shortest distance to go from i to j> # this matrix can be calculated for any given graph using> # all-pair shortest path algorithms> dist> => [[> 0> ,> 0> ,> 0> ,> 0> ,> 0> ], [> 0> ,> 0> ,> 10> ,> 15> ,> 20> ], [> > 0> ,> 10> ,> 0> ,> 25> ,> 25> ], [> 0> ,> 15> ,> 25> ,> 0> ,> 30> ], [> 0> ,> 20> ,> 25> ,> 30> ,> 0> ]]> # memoization for top down recursion> memo> => [[> -> 1> ]> *> (> 1> < < (n> +> 1> ))> for> _> in> range> (n> +> 1> )]> def> fun(i, mask):> > # base case> > # if only ith bit and 1st bit is set in our mask,> > # it implies we have visited all other nodes already> > if> mask> => => ((> 1> < < i) |> 3> ):> > return> dist[> 1> ][i]> > # memoization> > if> memo[i][mask] !> => -> 1> :> > return> memo[i][mask]> > res> => 10> *> *> 9> # result of this sub-problem> > # we have to travel all nodes j in mask and end the path at ith node> > # so for every node j in mask, recursively calculate cost of> > # travelling all nodes in mask> > # except i and then travel back from node j to node i taking> > # the shortest path take the minimum of all possible j nodes> > for> j> in> range> (> 1> , n> +> 1> ):> > if> (mask & (> 1> < < j)) !> => 0> and> j !> => i> and> j !> => 1> :> > res> => min> (res, fun(j, mask & (~(> 1> < < i)))> +> dist[j][i])> > memo[i][mask]> => res> # storing the minimum value> > return> res> # Driver program to test above logic> ans> => 10> *> *> 9> for> i> in> range> (> 1> , n> +> 1> ):> > # try to go from node 1 visiting all nodes in between to i> > # then return from i taking the shortest route to 1> > ans> => min> (ans, fun(i, (> 1> < < (n> +> 1> ))> -> 1> )> +> dist[i][> 1> ])> print> (> 'The cost of most efficient tour = '> +> str> (ans))> # This code is contributed by Serjeel Ranjan>

C#

using> System;> class> TSE> {> > // there are four nodes in example graph (graph is> > // 1-based)> > static> int> n = 4;> > // give appropriate maximum to avoid overflow> > static> int> MAX = 1000000;> > // dist[i][j] represents shortest distance to go from i> > // to j this matrix can be calculated for any given> > // graph using all-pair shortest path algorithms> > static> int> [, ] dist = { { 0, 0, 0, 0, 0 },> > { 0, 0, 10, 15, 20 },> > { 0, 10, 0, 25, 25 },> > { 0, 15, 25, 0, 30 },> > { 0, 20, 25, 30, 0 } };> > // memoization for top down recursion> > static> int> [, ] memo => new> int> [(n + 1), (1 < < (n + 1))];> > static> int> fun(> int> i,> int> mask)> > 3))> > return> dist[1, i];> > > // memoization> > if> (memo[i, mask] != 0)> > return> memo[i, mask];> > int> res = MAX;> // result of this sub-problem> > // we have to travel all nodes j in mask and end the> > // path at ith node so for every node j in mask,> > // recursively calculate cost of travelling all> > // nodes in mask> > // except i and then travel back from node j to node> > // i taking the shortest path take the minimum of> > // all possible j nodes> > for> (> int> j = 1; j <= n; j++)> > if> ((mask & (1 < < j)) != 0 && j != i && j != 1)> > res = Math.Min(res,> > fun(j, mask & (~(1 < < i)))> > + dist[j, i]);> > return> memo[i, mask] = res;> > > > // Driver program to test above logic> > public> static> void> Main()> > {> > int> ans = MAX;> > for> (> int> i = 1; i <= n; i++)> > // try to go from node 1 visiting all nodes in> > // between to i then return from i taking the> > // shortest route to 1> > ans = Math.Min(ans, fun(i, (1 < < (n + 1)) - 1)> > + dist[i, 1]);> > Console.WriteLine(> > 'The cost of most efficient tour = '> + ans);> > }> }> // This code is contributed by Tapesh(tapeshdua420)>

JavaScript

> // JavaScript code for the above approach> > // there are four nodes in example graph (graph is 1-based)> > let n = 4;> > > // give appropriate maximum to avoid overflow> > let MAX = 1000000;> > // dist[i][j] represents shortest distance to go from i to j> > // this matrix can be calculated for any given graph using> > // all-pair shortest path algorithms> > let dist = [> > [0, 0, 0, 0, 0], [0, 0, 10, 15, 20],> > [0, 10, 0, 25, 25], [0, 15, 25, 0, 30],> > [0, 20, 25, 30, 0],> > ];> > // memoization for top down recursion> > let memo => new> Array(n + 1);> > for> (let i = 0; i memo[i] = new Array(1 < < (n + 1)).fill(0) } function fun(i, mask) // base case // if only ith bit and 1st bit is set in our mask, // it implies we have visited all other nodes already if (mask == ((1 < < i) // Driver program to test above logic let ans = MAX; for (let i = 1; i <= n; i++) // try to go from node 1 visiting all nodes in // between to i then return from i taking the // shortest route to 1 ans = Math.min(ans, fun(i, (1 < < (n + 1)) - 1) + dist[i][1]); console.log('The cost of most efficient tour ' + ans); // This code is contributed by Potta Lokesh>

Wyjście

The cost of most efficient tour = 80 

Złożoność czasowa: O(n ² *2 ^N ) gdzie O(n* 2 ^N) to maksymalna liczba unikalnych podproblemów/stanów i O(n) dla przejścia (przez pętlę for jak w kodzie) w każdym stanie.

Przestrzeń pomocnicza: O(n*2 ^N ), gdzie n jest liczbą węzłów/miast tutaj.

Dla zbioru o rozmiarze n rozważamy n-2 podzbiory, każdy o rozmiarze n-1, tak że żaden z podzbiorów nie zawiera n-tego. Korzystając z powyższej relacji rekurencji, możemy napisać rozwiązanie oparte na programowaniu dynamicznym. Jest co najwyżej O(n*2 ^N ) podproblemów, a rozwiązanie każdego z nich wymaga liniowego czasu. Całkowity czas działania wynosi zatem O(n ² *2 ^N ). Złożoność czasowa jest znacznie mniejsza niż O(n!), ale nadal wykładnicza. Wymagana przestrzeń jest również wykładnicza. Zatem to podejście jest również niewykonalne nawet w przypadku nieco większej liczby wierzchołków. Wkrótce omówimy przybliżone algorytmy problemu komiwojażera.

Następny artykuł: Problem komiwojażera | Zestaw 2

Bibliografia:

http://www.lsi.upc.edu/~mjserna/docencia/algofib/P07/dynprog.pdf

http://www.cs.berkeley.edu/~vazirani/algorithms/chap6.pdf