Podobne i odmienne terminy algebraiczne: definicja i przykłady
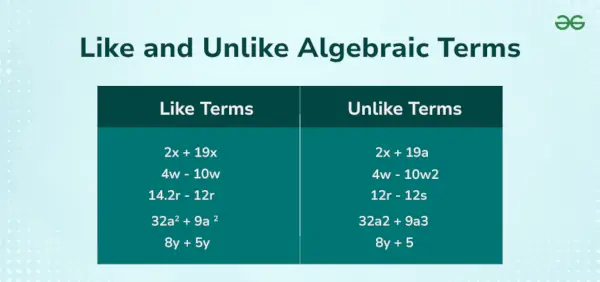
Terminy podobne to terminy w wyrażeniach algebraicznych, które mają te same zmienne podniesione do tych samych potęg. Terminy podobne i niepodobne to typy terminów w algebrze i możemy rozróżnić terminy podobne i odmienne, po prostu sprawdzając zmienne i ich potęgi. Terminy algebraiczne definiujemy jako pojedyncze wyrazy otrzymane z równania algebraicznego.

Na przykład w równaniu algebraicznym 5x + 3 lata 2 = 12 mamy trzy terminy, które są, 5x, 3y², I 12 . Tutaj, 5x, I 3 lata 2 są terminami zmiennymi, a 12 jest terminem stałym. Poniższy obraz przedstawia terminy podobne i niepodobne.
W tym artykule dowiemy się szczegółowo o terminach podobnych i odmiennych, ich przykładach, uproszczeniu i innych.
Podobne określenia
Terminy podobne to terminy, które mają te same zmienne, a moc każdej ze zmiennych jest również taka sama. Możemy łączyć podobne terminy, aby uprościć wyrażenia algebraiczne i można to bardzo łatwo obliczyć. Na przykład 3y + 5y jest wyrażeniem algebraicznym z podobnymi terminami 3y i 5y. Aby uprościć to wyrażenie algebraiczne, dodajemy podobne terminy. Zatem uproszczenie danego wyrażenia wynosi 8y.
Przykłady podobnych terminów
Terminy podobne to terminy, które mają tę samą zmienną o podobnej mocy. Oto kilka przykładów podobnych terminów:
- 40x 2 i 56xy 2 : W pierwszym przykładzie xy 2 jest wspólnym współczynnikiem dla obu wyrazów. Są więc jak terminy.
- 30z 2 i 18z 2 : z 2 jest wspólnym współczynnikiem dla obu wyrazów. Są więc jak terminy.
- 45abc i 29abc: abc jest wspólnym współczynnikiem dla obu wyrazów. Są więc jak terminy.
- 18r 3 i 38r 3 : R 3 jest wspólnym współczynnikiem dla obu wyrazów. Są więc jak terminy.
- 2xy i 8xy: xy jest wspólnym współczynnikiem dla obu terminów. Są więc jak terminy.
Dodawanie i odejmowanie podobnych terminów
Możemy łatwo wykonywać dodawanie i odejmowanie podobnych terminów i nie wymaga to żadnych specjalnych zasad. Zwykle są one uproszczone przy użyciu normalnych zasad dodawania i odejmowania. Możemy zrozumieć tę koncepcję na następującym przykładzie.
Przykład: Uprość 11x 3 + 5x 3
Rozwiązanie:
Jak widzimy, są one podobne do terminu, ponieważ mają podobne zmienne, a ich moc jest również stała.
Możemy łatwo dodać te terminy bezpośrednio.
= 11x 3 + 5x 3
= 16x 3
Jest to możliwe, ponieważ mają te same zmienne o podobnej mocy i można to rozumieć w ten sposób, że możemy bezpośrednio dodać rupie do rupii, czyli 5 Rs + 7 Rs to 12 Rs. Ale nie możemy bezpośrednio dodawać rupii do dolarów, a 5 Rs + 7 dolarów nie można bezpośrednio uprościć.
Podobnie, możemy również odjąć podobne terminy bezpośrednio, po prostu dodając, dodajemy podobne terminy, co można zrozumieć na podstawie poniższego przykładu.
Przykład 1: Uprość 11x 3 – 5x 3
Rozwiązanie:
Jak widzimy, są one podobne do terminu, ponieważ mają podobne zmienne, a ich moc jest również stała.
Możemy łatwo odjąć te terminy bezpośrednio.
= 11x 3 – 5x 3
= 6x 3
Przykład 2: Dodaj 3 X + 2 I + 5 i 4 X - 3 I + 7.
Rozwiązanie:
(3 X + 2 I + 5) + (4 X - 3 I + 7)
= (3 X + 4x) +(2 lata + (-3 lata))+ (5 + 7)
= 7 X − I + 12
W przeciwieństwie do Warunków
W przeciwieństwie do terminów, są to terminy z różnymi zmiennymi, a każda ze zmiennych może mieć różne wykładniki lub nie. Na przykład 9x + 6y jest wyrażeniem algebraicznym, w przeciwieństwie do terminów. Ponieważ ma dwie różne zmienne x i y.
Jeśli zmienne są różne, nie sprawdzamy potęgi, ponieważ w żaden sposób nie różnią się one od terminów, ale jeśli zmienne są takie same, sprawdzamy ich potęgi, ponieważ mogą, ale nie muszą, przypominać terminy.
Na przykład 5x 2 i 6x 2 są jak terminy, ale 5x 2 i 6x 3 różnią się od terminów.
Przykłady odmiennych terminów
W przeciwieństwie do terminów, są to terminy, które nie mają tych samych zmiennych ani podobnej mocy. Oto kilka przykładów odmiennych terminów:
- 40x 2 i 56xy: Tutaj, w jednym wyrażeniu algebraicznym, zmienną jest xy 2 a w drugim wyrażeniu algebraicznym zmienną jest xy. Obie zmienne są takie same, ale mają różne moce. Zatem różnią się one od terminów.
- 45abc i 29ab: Tutaj w jednym wyrażeniu algebraicznym zmienną jest abc, a w drugim wyrażeniu algebraicznym zmienna to ab. Obie zmienne są różne. Zatem należą one do kategorii, w przeciwieństwie do terminów.
Dodawanie i odejmowanie odmiennych terminów
Dodawanie i odejmowanie nie odbywa się pomiędzy, w przeciwieństwie do wyrazów, tzn. nie możemy dodawać ani odejmować w odróżnieniu od wyrazów i można to zrozumieć na przykładzie, ponieważ nie możemy dodać 5 litrów mleka na 6 kg ryżu. W ten sam sposób nie możemy dodawać ani odejmować, w przeciwieństwie do terminów.
Na przykład 3xy + 5x nie może być dalej rozwiązane i pozostaje w ten sam sposób.
Różnica między terminami podobnymi i odmiennymi
Różnice między podobnymi terminami i, w przeciwieństwie do terminów, omówiono w poniższej tabeli.
| Funkcja | Podobne określenia | W przeciwieństwie do Warunków |
|---|---|---|
| Definicja | Terminy podobne to terminy, które mają te same zmienne i te same wartości wykładników. | W przeciwieństwie do terminów, są to terminy, które mają różne zmienne i wykładniki. |
| Uproszczenie | Podobne terminy możemy łatwo uprościć. | W przeciwieństwie do terminów, których nie da się uprościć. |
| Łączenie terminów | Podobne terminy można bezpośrednio łączyć w celu wykonania obliczeń. | W przeciwieństwie do terminów, których nie można łączyć bezpośrednio, ponieważ reprezentują różne ilości |
| Dodawanie lub odejmowanie | Dodawanie i odejmowanie można osiągnąć w podobny sposób. | W przeciwieństwie do terminów nie możemy dodawać ani odejmować. |
| Przykłady | Przykładami podobnych terminów są: x 2 , 5x 2 , -11/3x 2 itp. | Przykładami terminów odmiennych są: x 2 i 5x 3 , -11/3x itd. |
Czytaj więcej
- Wyrażenia algebraiczne
- Rodzaje wyrażeń algebraicznych
Przykłady podobnych i odmiennych terminów algebraicznych
Przykład 1: Zidentyfikuj terminy podobne i różne od: 3x, 5xy, 18x 2 i 5x 3 , 29xy, 50x 3
Rozwiązanie:
Terminy podobne i odmienne z podanych terminów to:
Podobne określenia: (5xy, 29xy) i (5x 3 , 50x 3 )
W odróżnieniu od warunków: 3x, 18x 2 I
Przykład 2: Uprość 3xy + 5x 2 + 11ab – 4xy
Rozwiązanie:
Dane wyrażenie: 3xy + 5x 2 + 11ab – 4xy
Podobnie jak termin w danym wyrażeniu, 3xy i -4xy
O upraszczaniu,
= 3xy – 4xy + 5x 2 + 11ab
= -xy + 5x 2 + 11ab
Reszta wszystkich terminów różni się od terminów, więc nie można ich dalej rozwiązać.
Przykład 3: Uprość 8x + 15x 2 + 11x – 4x 2
Rozwiązanie:
Dane wyrażenie: 8x + 15x 2 + 11x – 4x 2
Podobnie jak termin w danym wyrażeniu, (8x, 11x) i (15x 2 , -4x 2 )
O upraszczaniu,
= 8x + 11x + 15x 2 – 4x 2
= 19x – 11x 2
Reszta wszystkich terminów różni się od terminów, więc nie można ich dalej rozwiązać.
Terminy algebraiczne podobne i odmienne – często zadawane pytania
Co to są terminy algebraiczne?
Wyrażenia algebraiczne to pojedyncze wyrazy otrzymane z równania algebraicznego, tj. wyrazy podzielone przez symbole operacji, takie jak + i -.
Jakie są terminy podobne i odmienne?
Terminy podobne i niepodobne są terminami wyrażeń algebraicznych. W podobny sposób mamy podobne zmienne, a moc wykładnika jest taka sama, podczas gdy w odmiennych terminach zmienne i ich moc są różne.
Jaka jest różnica między podobnymi i odmiennymi terminami algebraicznymi?
Podstawowa różnica między terminami podobnymi i odmiennymi polega na tym, że w tym samym terminie mamy tę samą zmienną o tych samych mocach, podczas gdy w przeciwieństwie do terminów mamy różne zmienne o różnych mocach.
Jak znaleźć podobne i niepodobne terminy algebraiczne?
Terminy podobne to terminy, które mają te same zmienne o tych samych potęgach, a terminy odmienne to terminy z różnymi zmiennymi i różnymi potęgami. Możemy je łatwo zidentyfikować po prostu sprawdzając zmienne.
Czy możemy dodawać lub odejmować wyrażenia algebraiczne?
Możemy łatwo dodawać lub odejmować podobne terminy, takie jak 5x i 11x. Są to terminy podobne i można je dodać jako 16x.
Czy możemy dodawać lub odejmować w przeciwieństwie do terminów algebraicznych?
Nie możemy dodawać ani odejmować w przeciwieństwie do terminów takich jak 2x i 3y. Zatem w przeciwieństwie do terminów nie można ich razem dodawać ani odejmować.