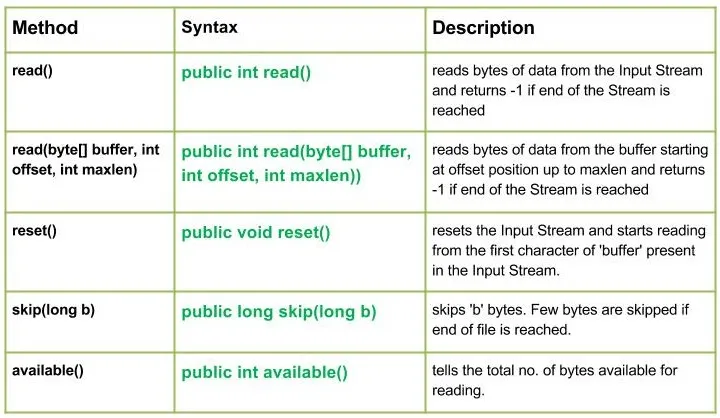
Kraty:

Niech L będzie niepustym zbiorem zamkniętym dwiema operacjami binarnymi zwanymi spotkaniem i złączeniem, oznaczonymi przez ∧ i ∨. Następnie L nazywa się kratą, jeśli obowiązują następujące aksjomaty, gdzie a, b, c są elementami w L:
1) Prawo przemienne: -
(a) za ∧ b = b ∧ za (b) za ∨ b = b ∨ a
2) Prawo stowarzyszeniowe: –
(a) (a ∧ b)∧ do = za ∧(b∧ do) (b) (a ∨ b) ∨ do = za ∨ (b ∨ do)
3) Prawo absorpcji: -
(a) za ∧ ( za ∨ b) = za (b) za ∨ ( za ∧ b) = za
Dwoistość:
Podwójność dowolnego stwierdzenia w siatce (L,∧,∨) definiuje się jako stwierdzenie uzyskane przez zamianę ∧ i ∨.
Na przykład , liczba podwójna a ∧ (b ∨ a) = a ∨ a to a ∨ (b ∧ a )= a ∧ a
Ograniczone kraty:
Sieć L nazywa się siecią ograniczoną, jeśli ma największy element 1 i najmniejszy element 0.
Przykład:
- Zbiór potęg P(S) zbioru S w ramach operacji przecięcia i sumy jest siatką ograniczoną, ponieważ ∅ jest najmniejszym elementem P(S), a zbiór S jest największym elementem P(S).
- Zbiór +ve liczby całkowitej I + w zwykłym porządku ≦ nie jest siatką ograniczoną, ponieważ ma najmniejszy element 1, ale największy element nie istnieje.
Właściwości ograniczonych krat:
Jeśli L jest siatką ograniczoną, to dla dowolnego elementu a ∈ L mamy następujące tożsamości:
- a ∨ 1 = 1
- a ∧1= a
- a ∨0=a
- a ∧0=0
Twierdzenie: Udowodnić, że każda skończona sieć L = {a 1 ,A 2 ,A 3 ....A N } jest ograniczona.
Dowód: Podaliśmy skończoną kratę:
L = {a 1 ,A 2 ,A 3 ....A N }
Zatem największym elementem krat L jest a 1 ∨ a 2 ∨ a 3∨.....∨a N .
Ponadto najmniejszym elementem sieci L jest a 1 ∧ a 2 ∧a 3 ∧....∧a N .
Ponieważ dla każdej skończonej sieci istnieją największe i najmniejsze elementy. Zatem L jest ograniczone.
Podsieci:
Rozważmy niepusty podzbiór L 1 siatki L. Następnie L 1 nazywa się podsiecią L, jeśli L 1 samo w sobie jest siecią, tj. działaniem L, tj. a ∨ b ∈ L 1 oraz a ∧ b ∈ L 1 kiedykolwiek a ∈ L 1 oraz b ∈ L 1 .
Przykład: Rozważmy kratę wszystkich +ve liczb całkowitych I + w ramach działania podzielności. Krata D N wszystkich dzielników n > 1 jest podsiecią I + .
Wyznacz wszystkie podsieci D 30 zawierające co najmniej cztery elementy, D 30 ={1,2,3,5,6,10,15,30}.
Rozwiązanie: Podsieci D 30 zawierające co najmniej cztery elementy, są następujące:
1. {1, 2, 6, 30} 2. {1, 2, 3, 30}
3. {1, 5, 15, 30} 4. {1, 3, 6, 30}
5. {1, 5, 10, 30} 6. {1, 3, 15, 30}
7. {2, 6, 10, 30}
Kraty izomorficzne:
Dwie kraty L 1 i ja 2 nazywane są kratami izomorficznymi, jeśli istnieje bijekcja z L 1 do L 2 tj. f: L 1 ⟶ L 2 , takie, że f (a ∧ b) =f(a)∧ f(b) i f (a ∨ b) = fa (a) ∨ f (b)
Przykład: Określ, czy sieci pokazane na rys. są izomorficzne.
Rozwiązanie: Kraty pokazane na rys. są izomorficzne. Rozważmy odwzorowanie f = {(a, 1), (b, 2), (c, 3), (d, 4)}. Na przykład f (b ∧ c) = f (a) = 1. Ponadto, my mieć f (b) ∧ f(c) = 2 ∧ 3 = 1

Krata rozdzielcza:
Sieć L nazywa się siecią rozdzielczą, jeśli dla dowolnych elementów a, b i c sieci L spełnia następujące własności rozdzielcze:
- za ∧ (b ∨ do) = (a ∧ b) ∨ (a ∧ do)
- za ∨ (b ∧ do) = (a ∨ b) ∧ (a ∨ do)
Jeżeli sieć L nie spełnia powyższych właściwości, nazywa się ją siecią nierozdzielną.
Przykład:
- Zbiór mocy P (S) zbioru S pod działaniem przecięcia i sumy jest funkcją rozdzielczą. Od,
za ∩ (b ∪ c) = (a ∩ b) ∪ (a ∩ do)
i także a ∪ (b ∩ c) = (a ∪ b) ∩ (a ∪c) dla dowolnych zbiorów a, b i c P(S). - Krata pokazana na rys. II jest rozdzielnicą. Ponieważ spełnia właściwości rozdzielcze dla wszystkich uporządkowanych trójek, które pochodzą z 1, 2, 3 i 4.

Uzupełnienia i uzupełnione kraty:
Niech L będzie kratą ograniczoną z dolną granicą o i górną granicą I. Niech a będzie elementem, jeśli L. Element x w L nazywa się dopełnieniem a, jeśli a ∨ x = I i a ∧ x = 0
Mówi się, że krata L jest uzupełniona, jeśli L jest ograniczona i każdy element w L ma dopełnienie.
Przykład: Określ uzupełnienie a i c na rys.:

Rozwiązanie: Dopełnieniem a jest d. Ponieważ a ∨ d = 1 i a ∧ d = 0
Dopełnienie c nie istnieje. Nie istnieje bowiem żaden element c taki, że c ∨ c'=1 i c ∧ c'= 0.
Krata modułowa:
Kratę (L, ∧,∨) nazywa się siecią modułową, jeśli a ∨ (b ∧ c) = (a ∨ b) ∧ c, gdy a ≦ c.
Bezpośredni produkt krat:
Niech (l 1 ∨ 1 ∧ 1 )i ja 2 ∨ 2 ∧ 2 ) będą dwiema kratami. Wtedy (L, ∧,∨) jest bezpośrednim iloczynem sieci, gdzie L = L 1 x L 2 w którym operacje binarne ∨(łączenie) i ∧(spotykanie) na L są takie, że dla dowolnego (a 1 ,B 1 ) i (a 2 ,B 2 ) w l.
(A 1 ,B 1 )∨(a 2 ,B 2 )=(a 1 ∨ 1 A 2 ,B 1 ∨ 2 B 2 )
i (a 1 ,B 1 ) ∧ ( a 2 ,B 2 )=(a 1 ∧ 1 A 2 ,B 1 ∧ 2 B 2 ).
Przykład: Rozważmy kratę (L, ≦), jak pokazano na ryc. gdzie L = {1, 2}. Wyznacz kraty (L 2 , ≦), gdzie L 2 = dł. x dł.

Rozwiązanie: Krata (L 2 , ≦) pokazano na rys.: