Nombre d'éléments avec des facteurs impairs dans une plage donnée

 #practiceLinkDiv { display : aucun !important; }
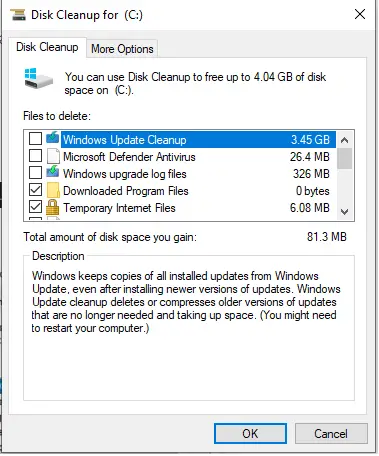
#practiceLinkDiv { display : aucun !important; } Étant donné une plage [ n m ] trouver le nombre d'éléments qui ont un nombre impair de facteurs dans la plage donnée ( n et m compris).
Exemples :
Input : n = 5 m = 100 Output : 8 The numbers with odd factors are 9 16 25 36 49 64 81 and 100 Input : n = 8 m = 65 Output : 6 Input : n = 10 m = 23500 Output : 150
UN Solution simple consiste à parcourir tous les nombres à partir de n . Pour chaque nombre, vérifiez s’il comporte un nombre pair de facteurs. S'il comporte un nombre pair de facteurs, incrémentez le nombre de ces nombres et imprimez enfin le nombre de ces éléments. Pour trouver efficacement tous les diviseurs d'un nombre naturel, reportez-vous Tous les diviseurs d'un nombre naturel
Un Solution efficace est d'observer le modèle. Seuls les chiffres qui sont Carrés parfaits avoir un nombre impair de facteurs. Analysons ce modèle à travers un exemple.
Par exemple, 9 a un nombre impair de facteurs 1 3 et 9. 16 a également un nombre impair de facteurs 1 2 4 8 16. La raison en est que pour les nombres autres que les carrés parfaits, tous les facteurs sont sous forme de paires, mais pour les carrés parfaits, un facteur est unique et rend le total impair.
Comment trouver le nombre de carrés parfaits dans une plage ?
La réponse est la différence entre la racine carrée de m et n-1 ( pas n )
Il y a une petite mise en garde. Comme les deux n et m sont inclusifs si n est un carré parfait, nous obtiendrons une réponse inférieure à la réponse réelle. Pour comprendre cela, considérons la plage [4 36]. La réponse est 5, c'est-à-dire les nombres 4 9 16 25 et 36.
Mais si nous faisons (36**0,5) - (4**0,5) nous obtenons 4. Donc pour éviter cette erreur sémantique nous prenons n-1 .
// C++ program to count number of odd squares // in given range [n m] #include using namespace std ; int countOddSquares ( int n int m ) { return ( int ) pow ( m 0.5 ) - ( int ) pow ( n -1 0.5 ); } // Driver code int main () { int n = 5 m = 100 ; cout < < 'Count is ' < < countOddSquares ( n m ); return 0 ; }
Java // Java program to count number of odd squares // in given range [n m] import java.io.* ; import java.util.* ; import java.lang.* ; class GFG { public static int countOddSquares ( int n int m ) { return ( int ) Math . pow (( double ) m 0.5 ) - ( int ) Math . pow (( double ) n - 1 0.5 ); } // Driver code for above functions public static void main ( String [] args ) { int n = 5 m = 100 ; System . out . print ( 'Count is ' + countOddSquares ( n m )); } } // Mohit Gupta_OMG <(o_0)>
Python3 # Python program to count number of odd squares # in given range [n m] def countOddSquares ( n m ): return int ( m ** 0.5 ) - int (( n - 1 ) ** 0.5 ) # Driver code n = 5 m = 100 print ( 'Count is' countOddSquares ( n m )) # Mohit Gupta_OMG <0_o>
C# // C# program to count number of odd // squares in given range [n m] using System ; class GFG { // Function to count odd squares public static int countOddSquares ( int n int m ) { return ( int ) Math . Pow (( double ) m 0.5 ) - ( int ) Math . Pow (( double ) n - 1 0.5 ); } // Driver code public static void Main () { int n = 5 m = 100 ; Console . Write ( 'Count is ' + countOddSquares ( n m )); } } // This code is contributed by Nitin Mittal.
PHP // PHP program to count // number of odd squares // in given range [n m] function countOddSquares ( $n $m ) { return pow ( $m 0.5 ) - pow ( $n - 1 0.5 ); } // Driver code $n = 5 ; $m = 100 ; echo 'Count is ' countOddSquares ( $n $m ); // This code is contributed // by nitin mittal. ?>
JavaScript < script > // JavaScript program to count number of odd squares // in given range [n m] function countOddSquares ( n m ) { return Math . pow ( m 0.5 ) - Math . pow ( n - 1 0.5 ); } // Driver Code let n = 5 m = 100 ; document . write ( 'Count is ' + countOddSquares ( n m )); < /script>
Sortir :
Count is 8
Complexité temporelle : O(1)
Espace auxiliaire : O(1)