POSTORDRE-GJENNOMGANG AV BINÆRT TRE

Postordregjennomgang er definert som en type kryssing av tre som følger Venstre-Høyre-Root-policyen slik at for hver node:

Det venstre undertreet krysses først

Deretter krysses det høyre undertreet

Til slutt krysses rotnoden til undertreet

Postordregjennomgang

Algoritme for postordergjennomgang av binært tre:

Algoritmen for postordre-traversering vises som følger:

Postordre (root):

Følg trinn 2 til 4 til root != NULL

Postordre (root -> venstre)

Postordre (root -> høyre)

Skriv root -> data

Sluttløkke

Hvordan fungerer Postorder Traversal of Binary Tree?

Tenk på følgende tre:

Eksempel på binært tre

Hvis vi utfører en postorder-traversering i dette binære treet, vil traverseringen være som følger:

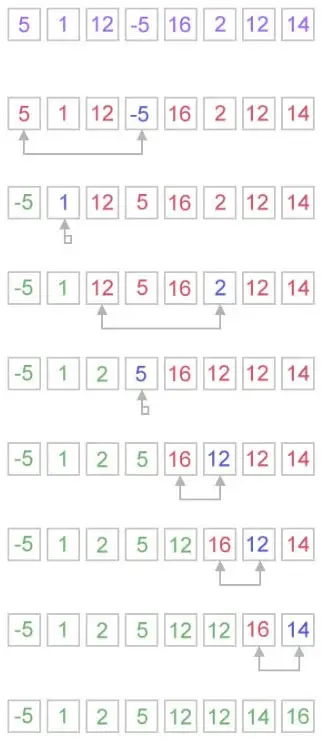
Trinn 1: Traverseringen vil gå fra 1 til venstre undertre dvs. 2, deretter fra 2 til venstre undertrerot, dvs. 4. Nå har 4 ikke noe undertre, så det vil bli besøkt.

Node 4 er besøkt

Steg 2: Ettersom venstre undertre av 2 besøkes fullstendig, vil det nå krysse høyre undertre av 2, dvs. det vil flytte til 5. Siden det ikke er noe undertre på 5, vil det bli besøkt.

Node 5 er besøkt

Trinn 3: Nå er både venstre og høyre undertre av node 2 besøkt. Så besøk node 2 selv.

Node 2 er besøkt

Trinn 4: Når det venstre undertreet til node 1 krysses, vil det nå flytte til høyre undertrerot, dvs. 3. Node 3 har ikke noe venstre undertre, så det vil krysse det høyre undertreet, dvs. 6. Node 6 har ikke noe undertre og så det er besøkt.

Node 6 er besøkt

Trinn 5: Alle undertrærne til node 3 krysses. Så nå er node 3 besøkt.

Node 3 er besøkt

Trinn 6: Ettersom alle undertrærne til node 1 krysses, er det nå på tide at node 1 skal besøkes og kryssingen avsluttes etter det når hele treet krysses.

Hele treet er besøkt

Så rekkefølgen for kryssing av noder er 4 -> 5 -> 2 -> 6 -> 3 -> 1 .

Program for å implementere Postorder Traversal of Binary Tree

Nedenfor er kodeimplementeringen av postordre-traverseringen:

C++

// C++ program for postorder traversals> #include> using> namespace> std;> // Structure of a Binary Tree Node> struct> Node {> > int> data;> > struct> Node *left, *right;> > Node(> int> v)> > {> > data = v;> > left = right = NULL;> > }> };> // Function to print postorder traversal> void> printPostorder(> struct> Node* node)> {> > if> (node == NULL)> > return> ;> > // First recur on left subtree> > printPostorder(node->venstre);> > // Then recur on right subtree> > printPostorder(node->høyre);> > // Now deal with the node> >

cout ' '; } // Driver code int main() {  struct Node* root = new Node(1);  root->venstre = ny node(2);  root->right = ny node(3);  root->venstre->venstre = ny node(4);  root->venstre->høyre = ny node(5);  root->right->right = ny node(6);  // Function call cout < < 'Postorder traversal of binary tree is: 
';  printPostorder(root);  return 0; }>

Java

// Java program for postorder traversals> import> java.util.*;> // Structure of a Binary Tree Node> class> Node {> > int> data;> > Node left, right;> > Node(> int> v)> > {> > data = v;> > left = right => null> ;> > }> }> class> GFG {> > > // Function to print postorder traversal> > static> void> printPostorder(Node node)> > {> > if> (node ==> null> )> > return> ;> > // First recur on left subtree> > printPostorder(node.left);> > // Then recur on right subtree> > printPostorder(node.right);> > // Now deal with the node> > System.out.print(node.data +> ' '> );> > }> > // Driver code> > public> static> void> main(String[] args)> > {> > Node root => new> Node(> 1> );> > root.left => new> Node(> 2> );> > root.right => new> Node(> 3> );> > root.left.left => new> Node(> 4> );> > root.left.right => new> Node(> 5> );> > root.right.right => new> Node(> 6> );> > // Function call> > System.out.println(> 'Postorder traversal of binary tree is: '> );> > printPostorder(root);> > }> }> // This code is contributed by prasad264>

Python3

# Python program for postorder traversals> # Structure of a Binary Tree Node> class> Node:> > def> __init__(> self> , v):> > self> .data> => v> > self> .left> => None> > self> .right> => None> # Function to print postorder traversal> def> printPostorder(node):> > if> node> => => None> :> > return> > # First recur on left subtree> > printPostorder(node.left)> > # Then recur on right subtree> > printPostorder(node.right)> > # Now deal with the node> > print> (node.data, end> => ' '> )> # Driver code> if> __name__> => => '__main__'> :> > root> => Node(> 1> )> > root.left> => Node(> 2> )> > root.right> => Node(> 3> )> > root.left.left> => Node(> 4> )> > root.left.right> => Node(> 5> )> > root.right.right> => Node(> 6> )> > # Function call> > print> (> 'Postorder traversal of binary tree is:'> )> > printPostorder(root)>

C#

// C# program for postorder traversals> using> System;> // Structure of a Binary Tree Node> public> class> Node {> > public> int> data;> > public> Node left, right;> > public> Node(> int> v)> > {> > data = v;> > left = right => null> ;> > }> }> public> class> GFG {> > // Function to print postorder traversal> > static> void> printPostorder(Node node)> > {> > if> (node ==> null> )> > return> ;> > // First recur on left subtree> > printPostorder(node.left);> > // Then recur on right subtree> > printPostorder(node.right);> > // Now deal with the node> > Console.Write(node.data +> ' '> );> > }> > static> public> void> Main()> > {> > // Code> > Node root => new> Node(1);> > root.left => new> Node(2);> > root.right => new> Node(3);> > root.left.left => new> Node(4);> > root.left.right => new> Node(5);> > root.right.right => new> Node(6);> > // Function call> > Console.WriteLine(> > 'Postorder traversal of binary tree is: '> );> > printPostorder(root);> > }> }> // This code is contributed by karthik.>

Javascript

// Structure of a Binary Tree Node> class Node {> > constructor(v) {> > this> .data = v;> > this> .left => null> ;> > this> .right => null> ;> > }> }> // Function to print postorder traversal> function> printPostorder(node) {> > if> (node ==> null> ) {> > return> ;> > }> > // First recur on left subtree> > printPostorder(node.left);> > // Then recur on right subtree> > printPostorder(node.right);> > // Now deal with the node> > console.log(node.data +> ' '> );> }> // Driver code> function> main() {> > let root => new> Node(1);> > root.left => new> Node(2);> > root.right => new> Node(3);> > root.left.left => new> Node(4);> > root.left.right => new> Node(5);> > root.right.right => new> Node(6);> > // Function call> > console.log(>

'Postorder traversal of binary tree is: 
'>

);> > printPostorder(root);> }> main();>

Produksjon

Postorder traversal of binary tree is: 4 5 2 6 3 1

Forklaring:

Hvordan postordreovergang fungerer

Kompleksitetsanalyse:

Tidskompleksitet: O(N) hvor N er det totale antallet noder. Fordi den krysser alle nodene minst én gang.
Hjelpeplass: O(1) hvis ingen rekursjonsstabelplass vurderes. Ellers O(h) hvor h er høyden på treet