Tilbakesporingsalgoritmer er som problemløsningsstrategier som hjelper til med å utforske ulike alternativer for å finne den beste løsningen. De jobber ved å prøve ut forskjellige veier, og hvis en ikke fungerer, går de tilbake og prøver en annen til de finner den rette. Det er som å løse et puslespill ved å teste forskjellige brikker til de passer perfekt sammen.

Tilbakesporing

Innholdsfortegnelse

• Hva er tilbakesporingsalgoritme?
• Hvordan fungerer en tilbakesporingsalgoritme?
• Eksempel på tilbakesporingsalgoritme
• Når skal jeg bruke en tilbakesporingsalgoritme?
• Anvendelser av tilbakesporingsalgoritme
• Grunnleggende om tilbakesporingsalgoritme
• Standardproblemer på tilbakesporingsalgoritme
• Enkle problemer med tilbakesporingsalgoritme
• Middels problemer med tilbakesporingsalgoritme
• Harde problemer med tilbakesporingsalgoritme

Hva er tilbakesporingsalgoritme?

Tilbakesporing er en problemløsende algoritmisk teknikk som innebærer å finne en løsning trinnvis ved å prøve ulike alternativer og angre dem hvis de fører til en blindvei .

Det brukes ofte i situasjoner der du trenger å utforske flere muligheter for å løse et problem, som å søke etter en sti i en labyrint eller løse gåter som Sudoku . Når en blindvei er nådd, går algoritmen tilbake til forrige beslutningspunkt og utforsker en annen vei til en løsning er funnet eller alle muligheter er uttømt.

Hvordan fungerer en tilbakesporingsalgoritme?

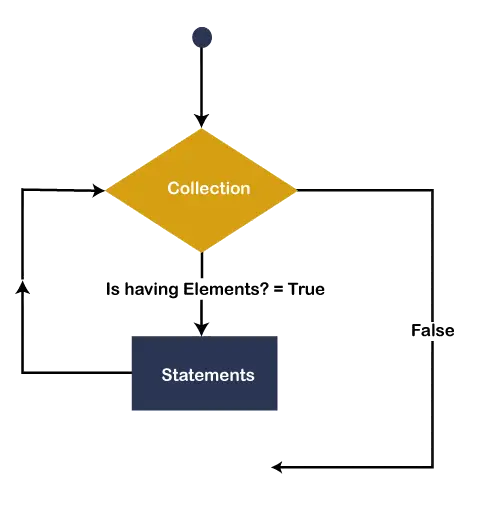
EN tilbakesporingsalgoritme fungerer ved å rekursivt utforske alle mulige løsninger på et problem. Den starter med å velge en innledende løsning, og deretter utforsker den alle mulige utvidelser av den løsningen. Hvis en utvidelse fører til en løsning, returnerer algoritmen den løsningen. Hvis en utvidelse ikke fører til en løsning, går algoritmen tilbake til den forrige løsningen og prøver en annen utvidelse.

Følgende er en generell oversikt over hvordan en tilbakesporingsalgoritme fungerer:

1. Velg en innledende løsning.
2. Utforsk alle mulige utvidelser av gjeldende løsning.
3. Hvis en utvidelse fører til en løsning, returner den løsningen.
4. Hvis en utvidelse ikke fører til en løsning, gå tilbake til forrige løsning og prøv en annen utvidelse.
5. Gjenta trinn 2-4 til alle mulige løsninger er utforsket.

Eksempel på tilbakesporingsalgoritme

Eksempel: Finne den korteste veien gjennom en labyrint

Inndata: En labyrint representert som en 2D-array, hvor 0 representerer et åpent rom og 1 representerer en vegg.

Algoritme:

1. Start ved startpunktet.
2. For hver av de fire mulige retningene (opp, ned, venstre, høyre), prøv å bevege deg i den retningen.
3. Hvis bevegelse i den retningen fører til endepunktet, returner stien som er tatt.
4. Hvis flytting i den retningen ikke fører til endepunktet, gå tilbake til forrige posisjon og prøv en annen retning.
5. Gjenta trinn 2-4 til endepunktet er nådd eller alle mulige stier er utforsket.

Når skal jeg bruke en tilbakesporingsalgoritme?

Tilbakesporingsalgoritmer brukes best til å løse problemer som har følgende egenskaper:

• Det er flere mulige løsninger på problemet.
• Problemet kan brytes ned i mindre delproblemer.
• Delproblemene kan løses selvstendig.

Anvendelser av Backtracking Algorithm

Tilbakesporingsalgoritmer brukes i en lang rekke applikasjoner, inkludert:

• Løse gåter (f.eks. Sudoku, kryssord)
• Finne den korteste veien gjennom en labyrint
• Planleggingsproblemer
• Problemer med ressursfordeling
• Problemer med nettverksoptimalisering

Grunnleggende om tilbakesporingsalgoritme:

• Forskjellen mellom Backtracking og Branch-N-Bound-teknikk
• Hva er forskjellen mellom tilbakesporing og rekursjon?

Standardproblemer på tilbakesporingsalgoritme:

• Ridderens turproblem
• Rotte i en labyrint
• N Queen Problem | Tilbakesporing-3
• Delmengde Sum problem
• m Fargeproblem
• Hamiltonsk syklus
• Sudoku | Tilbakesporing-7
• Magnet puslespill
• Fjern ugyldige parenteser
• En tilbakesporende tilnærming for å generere n-bits gråkoder
• Skriv et program for å skrive ut alle permutasjoner av en gitt streng

Enkle problemer med tilbakesporingsalgoritme:

• Tilbakesporing for å finne alle undersett
• Sjekk om en gitt streng er sum-streng
• Tell alle mulige veier mellom to toppunkter
• Finn alle distinkte undergrupper av et gitt sett
• Finn om det er en bane med mer enn k lengde fra en kilde
• Skriv ut alle stier fra en gitt kilde til en destinasjon
• Skriv ut alle mulige strenger som kan lages ved å plassere mellomrom

Middels problemer med tilbakesporingsalgoritme:

• Tautrekking
• 8 dronninger problem
• Kombinasjonssum
• Warnsdorffs algoritme for Knights turproblem
• Finn stier fra hjørnecelle til midtcelle i labyrint
• Finn maksimalt mulig antall ved å gjøre maks K-bytter
• Rotte i en labyrint med flere trinn eller hopp tillatt
• N Queen i O(n) plass

Vanskelige problemer med tilbakesporingsalgoritme:

• Power Sett i leksikografisk rekkefølge
• Word Break Problem ved bruk av Backtracking
• Deling av et sett i K delmengder med lik sum
• Lengst mulig rute i en matrise med hindringer
• Finn korteste sikre rute i en sti med landminer
• Skriv ut alle palindromiske partisjoner av en streng
• Skriver ut alle løsninger i N-Queen Problem
• Skriv ut alle lengste vanlige undersekvenser i leksikografisk rekkefølge

Hurtigkoblinger :

• Lær datastruktur og algoritmer | DSA veiledning
• Topp 20 Intervjuspørsmål for Backtracking Algoritme
• «Videoer» på Backtracking