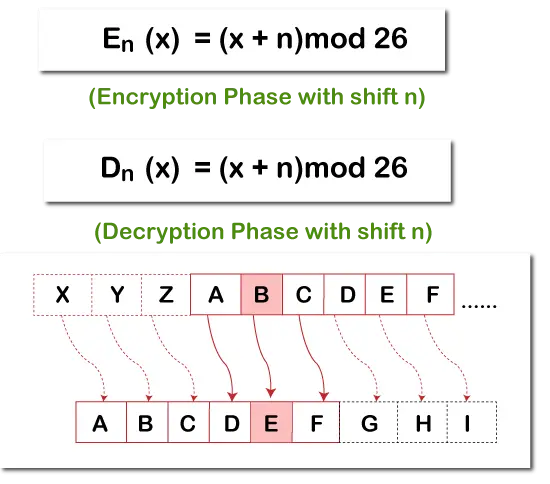
Minimum antall slettinger for å lage en sortert sekvens

 #practiceLinkDiv { display: ingen !viktig; }
#practiceLinkDiv { display: ingen !viktig; } Gitt en matrise med n heltall. Oppgaven er å fjerne eller slette minimum antall elementer fra matrisen slik at når de gjenværende elementene plasseres i samme rekkefølge for å danne en økende sortert sekvens .
Eksempler:
Input : {5 6 1 7 4}
Output : 2
Removing 1 and 4
leaves the remaining sequence order as
5 6 7 which is a sorted sequence.
Input : {30 40 2 5 1 7 45 50 8}
Output : 4
Recommended Practice Minimum antall slettinger for å lage en sortert sekvens Prøv det!
EN enkel løsning er å fjerne alle etterfølger en etter en og sjekk om gjenværende sett med elementer er i sortert rekkefølge eller ikke. Tidskompleksiteten til denne løsningen er eksponentiell.An effektiv tilnærming bruker begrepet finne lengden på den lengste økende undersekvensen av en gitt sekvens.
Algoritme:
--> arr be the given array.
--> n number of elements in arr .
--> len be the length of longest
increasing subsequence in arr .
-->// minimum number of deletions
min = n - len
C++Java// C++ implementation to find // minimum number of deletions // to make a sorted sequence #includeusing namespace std ; /* lis() returns the length of the longest increasing subsequence in arr[] of size n */ int lis ( int arr [] int n ) { int result = 0 ; int lis [ n ]; /* Initialize LIS values for all indexes */ for ( int i = 0 ; i < n ; i ++ ) lis [ i ] = 1 ; /* Compute optimized LIS values in bottom up manner */ for ( int i = 1 ; i < n ; i ++ ) for ( int j = 0 ; j < i ; j ++ ) if ( arr [ i ] > arr [ j ] && lis [ i ] < lis [ j ] + 1 ) lis [ i ] = lis [ j ] + 1 ; /* Pick resultimum of all LIS values */ for ( int i = 0 ; i < n ; i ++ ) if ( result < lis [ i ]) result = lis [ i ]; return result ; } // function to calculate minimum // number of deletions int minimumNumberOfDeletions ( int arr [] int n ) { // Find longest increasing // subsequence int len = lis ( arr n ); // After removing elements // other than the lis we // get sorted sequence. return ( n - len ); } // Driver Code int main () { int arr [] = { 30 40 2 5 1 7 45 50 8 }; int n = sizeof ( arr ) / sizeof ( arr [ 0 ]); cout < < 'Minimum number of deletions = ' < < minimumNumberOfDeletions ( arr n ); return 0 ; } Python3// Java implementation to find // minimum number of deletions // to make a sorted sequence class GFG { /* lis() returns the length of the longest increasing subsequence in arr[] of size n */ static int lis ( int arr [] int n ) { int result = 0 ; int [] lis = new int [ n ] ; /* Initialize LIS values for all indexes */ for ( int i = 0 ; i < n ; i ++ ) lis [ i ] = 1 ; /* Compute optimized LIS values in bottom up manner */ for ( int i = 1 ; i < n ; i ++ ) for ( int j = 0 ; j < i ; j ++ ) if ( arr [ i ] > arr [ j ] && lis [ i ] < lis [ j ] + 1 ) lis [ i ] = lis [ j ] + 1 ; /* Pick resultimum of all LIS values */ for ( int i = 0 ; i < n ; i ++ ) if ( result < lis [ i ] ) result = lis [ i ] ; return result ; } // function to calculate minimum // number of deletions static int minimumNumberOfDeletions ( int arr [] int n ) { // Find longest // increasing subsequence int len = lis ( arr n ); // After removing elements // other than the lis we get // sorted sequence. return ( n - len ); } // Driver Code public static void main ( String [] args ) { int arr [] = { 30 40 2 5 1 7 45 50 8 }; int n = arr . length ; System . out . println ( 'Minimum number of' + ' deletions = ' + minimumNumberOfDeletions ( arr n )); } } /* This code is contributed by Harsh Agarwal */C## Python3 implementation to find # minimum number of deletions to # make a sorted sequence # lis() returns the length # of the longest increasing # subsequence in arr[] of size n def lis ( arr n ): result = 0 lis = [ 0 for i in range ( n )] # Initialize LIS values # for all indexes for i in range ( n ): lis [ i ] = 1 # Compute optimized LIS values # in bottom up manner for i in range ( 1 n ): for j in range ( i ): if ( arr [ i ] > arr [ j ] and lis [ i ] < lis [ j ] + 1 ): lis [ i ] = lis [ j ] + 1 # Pick resultimum # of all LIS values for i in range ( n ): if ( result < lis [ i ]): result = lis [ i ] return result # Function to calculate minimum # number of deletions def minimumNumberOfDeletions ( arr n ): # Find longest increasing # subsequence len = lis ( arr n ) # After removing elements # other than the lis we # get sorted sequence. return ( n - len ) # Driver Code arr = [ 30 40 2 5 1 7 45 50 8 ] n = len ( arr ) print ( 'Minimum number of deletions = ' minimumNumberOfDeletions ( arr n )) # This code is contributed by Anant Agarwal.JavaScript// C# implementation to find // minimum number of deletions // to make a sorted sequence using System ; class GfG { /* lis() returns the length of the longest increasing subsequence in arr[] of size n */ static int lis ( int [] arr int n ) { int result = 0 ; int [] lis = new int [ n ]; /* Initialize LIS values for all indexes */ for ( int i = 0 ; i < n ; i ++ ) lis [ i ] = 1 ; /* Compute optimized LIS values in bottom up manner */ for ( int i = 1 ; i < n ; i ++ ) for ( int j = 0 ; j < i ; j ++ ) if ( arr [ i ] > arr [ j ] && lis [ i ] < lis [ j ] + 1 ) lis [ i ] = lis [ j ] + 1 ; /* Pick resultimum of all LIS values */ for ( int i = 0 ; i < n ; i ++ ) if ( result < lis [ i ]) result = lis [ i ]; return result ; } // function to calculate minimum // number of deletions static int minimumNumberOfDeletions ( int [] arr int n ) { // Find longest increasing // subsequence int len = lis ( arr n ); // After removing elements other // than the lis we get sorted // sequence. return ( n - len ); } // Driver Code public static void Main ( String [] args ) { int [] arr = { 30 40 2 5 1 7 45 50 8 }; int n = arr . Length ; Console . Write ( 'Minimum number of' + ' deletions = ' + minimumNumberOfDeletions ( arr n )); } } // This code is contributed by parashar.PHP< script > // javascript implementation to find // minimum number of deletions // to make a sorted sequence /* lis() returns the length of the longest increasing subsequence in arr[] of size n */ function lis ( arr n ) { let result = 0 ; let lis = new Array ( n ); /* Initialize LIS values for all indexes */ for ( let i = 0 ; i < n ; i ++ ) lis [ i ] = 1 ; /* Compute optimized LIS values in bottom up manner */ for ( let i = 1 ; i < n ; i ++ ) for ( let j = 0 ; j < i ; j ++ ) if ( arr [ i ] > arr [ j ] && lis [ i ] < lis [ j ] + 1 ) lis [ i ] = lis [ j ] + 1 ; /* Pick resultimum of all LIS values */ for ( let i = 0 ; i < n ; i ++ ) if ( result < lis [ i ]) result = lis [ i ]; return result ; } // function to calculate minimum // number of deletions function minimumNumberOfDeletions ( arr n ) { // Find longest increasing // subsequence let len = lis ( arr n ); // After removing elements // other than the lis we // get sorted sequence. return ( n - len ); } let arr = [ 30 40 2 5 1 7 45 50 8 ]; let n = arr . length ; document . write ( 'Minimum number of deletions = ' + minimumNumberOfDeletions ( arr n )); // This code is contributed by vaibhavrabadiya117. < /script>
ProduksjonMinimum number of deletions = 4Tidskompleksitet: På 2 )
Hjelpeplass: På)Tidskompleksiteten kan reduseres til O(nlogn) ved å finne Lengst økende undersekvensstørrelse (N Logg N)
Denne artikkelen er bidratt av Ayush Jauhari .
Tilnærming #2: Bruker lengst økende undersekvens
En tilnærming for å løse dette problemet er å finne lengden på den lengste økende undersekvensen (LIS) til den gitte matrisen og trekke den fra lengden på matrisen. Forskjellen gir oss det minste antallet slettinger som kreves for å gjøre matrisen sortert.
Algoritme
1. Beregn lengden på den lengste økende undersekvensen (LIS) av matrisen.
C++
2. Trekk fra lengden på LIS fra lengden på matrisen.
3. Returner differansen oppnådd i trinn 2 som utdata.Java#include#include #include // Required for max_element using namespace std ; // Function to find the minimum number of deletions int minDeletions ( vector < int > arr ) { int n = arr . size (); vector < int > lis ( n 1 ); // Initialize LIS array with 1 // Calculate LIS values for ( int i = 1 ; i < n ; ++ i ) { for ( int j = 0 ; j < i ; ++ j ) { if ( arr [ i ] > arr [ j ]) { lis [ i ] = max ( lis [ i ] lis [ j ] + 1 ); // Update LIS value } } } // Find the maximum length of LIS int maxLength = * max_element ( lis . begin () lis . end ()); // Return the minimum number of deletions return n - maxLength ; } //Driver code int main () { vector < int > arr = { 5 6 1 7 4 }; // Call the minDeletions function and print the result cout < < minDeletions ( arr ) < < endl ; return 0 ; } Python3import java.util.Arrays ; public class Main { public static int minDeletions ( int [] arr ) { int n = arr . length ; int [] lis = new int [ n ] ; Arrays . fill ( lis 1 ); // Initialize the LIS array with all 1's for ( int i = 1 ; i < n ; i ++ ) { for ( int j = 0 ; j < i ; j ++ ) { if ( arr [ i ] > arr [ j ] ) { lis [ i ] = Math . max ( lis [ i ] lis [ j ] + 1 ); } } } return n - Arrays . stream ( lis ). max (). getAsInt (); // Return the number of elements to delete } public static void main ( String [] args ) { int [] arr = { 5 6 1 7 4 }; System . out . println ( minDeletions ( arr )); // Output: 2 } }C#def min_deletions ( arr ): n = len ( arr ) lis = [ 1 ] * n for i in range ( 1 n ): for j in range ( i ): if arr [ i ] > arr [ j ]: lis [ i ] = max ( lis [ i ] lis [ j ] + 1 ) return n - max ( lis ) arr = [ 5 6 1 7 4 ] print ( min_deletions ( arr ))JavaScriptusing System ; using System.Collections.Generic ; using System.Linq ; namespace MinDeletionsExample { class Program { static int MinDeletions ( List < int > arr ) { int n = arr . Count ; List < int > lis = Enumerable . Repeat ( 1 n ). ToList (); // Initialize LIS array with 1 // Calculate LIS values for ( int i = 1 ; i < n ; ++ i ) { for ( int j = 0 ; j < i ; ++ j ) { if ( arr [ i ] > arr [ j ]) { lis [ i ] = Math . Max ( lis [ i ] lis [ j ] + 1 ); // Update LIS value } } } // Find the maximum length of LIS int maxLength = lis . Max (); // Return the minimum number of deletions return n - maxLength ; } // Driver Code static void Main ( string [] args ) { List < int > arr = new List < int > { 5 6 1 7 4 }; // Call the MinDeletions function and print the result Console . WriteLine ( MinDeletions ( arr )); // Keep console window open until a key is pressed Console . ReadKey (); } } }
Produksjon2Tidskompleksitet: O(n^2) der n er lengden på matrisen
Romkompleksitet: O(n) der n er lengden på arrayenTilnærming #3: Bruke binært søk
Denne tilnærmingen bruker binært søk for å finne riktig posisjon for å sette inn et gitt element i undersekvensen.
Algoritme
1. Initialiser en liste 'sub' med det første elementet i inndatalisten.
C++
2. For hvert påfølgende element i inndatalisten hvis det er større enn det siste elementet i 'sub', legg det til 'sub'.
3. Ellers bruk binært søk for å finne riktig posisjon for å sette inn elementet i 'sub'.
4. Minimum antall slettinger som kreves er lik lengden på inndatalisten minus lengden på 'sub'.Java#include#include using namespace std ; // Function to find the minimum number of deletions to make a strictly increasing subsequence int minDeletions ( vector < int >& arr ) { int n = arr . size (); vector < int > sub ; // Stores the longest increasing subsequence sub . push_back ( arr [ 0 ]); // Initialize the subsequence with the first element of the array for ( int i = 1 ; i < n ; i ++ ) { if ( arr [ i ] > sub . back ()) { // If the current element is greater than the last element of the subsequence // it can be added to the subsequence to make it longer. sub . push_back ( arr [ i ]); } else { int index = -1 ; // Initialize index to -1 int val = arr [ i ]; // Current element value int l = 0 r = sub . size () - 1 ; // Initialize left and right pointers for binary search // Binary search to find the index where the current element can be placed in the subsequence while ( l <= r ) { int mid = ( l + r ) / 2 ; // Calculate the middle index if ( sub [ mid ] >= val ) { index = mid ; // Update the index if the middle element is greater or equal to the current element r = mid - 1 ; // Move the right pointer to mid - 1 } else { l = mid + 1 ; // Move the left pointer to mid + 1 } } if ( index != -1 ) { sub [ index ] = val ; // Replace the element at the found index with the current element } } } // The minimum number of deletions is equal to the difference between the input array size and the size of the longest increasing subsequence return n - sub . size (); } int main () { vector < int > arr = { 30 40 2 5 1 7 45 50 8 }; int output = minDeletions ( arr ); cout < < output < < endl ; return 0 ; } Python3import java.util.ArrayList ; public class Main { // Function to find the minimum number of deletions to make a strictly increasing subsequence static int minDeletions ( ArrayList < Integer > arr ) { int n = arr . size (); ArrayList < Integer > sub = new ArrayList <> (); // Stores the longest increasing subsequence sub . add ( arr . get ( 0 )); // Initialize the subsequence with the first element of the array for ( int i = 1 ; i < n ; i ++ ) { if ( arr . get ( i ) > sub . get ( sub . size () - 1 )) { // If the current element is greater than the last element of the subsequence // it can be added to the subsequence to make it longer. sub . add ( arr . get ( i )); } else { int index = - 1 ; // Initialize index to -1 int val = arr . get ( i ); // Current element value int l = 0 r = sub . size () - 1 ; // Initialize left and right pointers for binary search // Binary search to find the index where the current element can be placed in the subsequence while ( l <= r ) { int mid = ( l + r ) / 2 ; // Calculate the middle index if ( sub . get ( mid ) >= val ) { index = mid ; // Update the index if the middle element is greater or equal to the current element r = mid - 1 ; // Move the right pointer to mid - 1 } else { l = mid + 1 ; // Move the left pointer to mid + 1 } } if ( index != - 1 ) { sub . set ( index val ); // Replace the element at the found index with the current element } } } // The minimum number of deletions is equal to the difference between the input array size and the size of the longest increasing subsequence return n - sub . size (); } public static void main ( String [] args ) { ArrayList < Integer > arr = new ArrayList <> (); arr . add ( 30 ); arr . add ( 40 ); arr . add ( 2 ); arr . add ( 5 ); arr . add ( 1 ); arr . add ( 7 ); arr . add ( 45 ); arr . add ( 50 ); arr . add ( 8 ); int output = minDeletions ( arr ); System . out . println ( output ); } }C#def min_deletions ( arr ): def ceil_index ( sub val ): l r = 0 len ( sub ) - 1 while l <= r : mid = ( l + r ) // 2 if sub [ mid ] >= val : r = mid - 1 else : l = mid + 1 return l sub = [ arr [ 0 ]] for i in range ( 1 len ( arr )): if arr [ i ] > sub [ - 1 ]: sub . append ( arr [ i ]) else : sub [ ceil_index ( sub arr [ i ])] = arr [ i ] return len ( arr ) - len ( sub ) arr = [ 30 40 2 5 1 7 45 50 8 ] output = min_deletions ( arr ) print ( output )JavaScriptusing System ; using System.Collections.Generic ; class Program { // Function to find the minimum number of deletions to make a strictly increasing subsequence static int MinDeletions ( List < int > arr ) { int n = arr . Count ; List < int > sub = new List < int > (); // Stores the longest increasing subsequence sub . Add ( arr [ 0 ]); // Initialize the subsequence with the first element of the array for ( int i = 1 ; i < n ; i ++ ) { if ( arr [ i ] > sub [ sub . Count - 1 ]) { // If the current element is greater than the last element of the subsequence // it can be added to the subsequence to make it longer. sub . Add ( arr [ i ]); } else { int index = - 1 ; // Initialize index to -1 int val = arr [ i ]; // Current element value int l = 0 r = sub . Count - 1 ; // Initialize left and right // pointers for binary search // Binary search to find the index where the current element // can be placed in the subsequence while ( l <= r ) { int mid = ( l + r ) / 2 ; // Calculate the middle index if ( sub [ mid ] >= val ) { index = mid ; // Update the index if the middle element is // greater or equal to the current element r = mid - 1 ; // Move the right pointer to mid - 1 } else { l = mid + 1 ; // Move the left pointer to mid + 1 } } if ( index != - 1 ) { sub [ index ] = val ; // Replace the element at the found index // with the current element } } } // The minimum number of deletions is equal to the difference // between the input list size and the size of the // longest increasing subsequence return n - sub . Count ; } // Driver code static void Main () { List < int > arr = new List < int > { 30 40 2 5 1 7 45 50 8 }; int output = MinDeletions ( arr ); Console . WriteLine ( output ); Console . ReadLine (); } }
Produksjon4Tidskompleksitet: O(n log n)
Hjelpeområde: O(n)
Lag quiz