Finn maksimal lengde slangesekvens
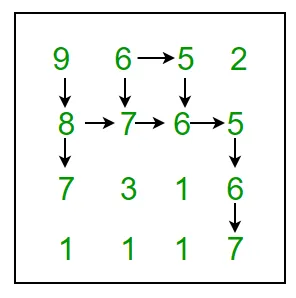
Gitt et rutenett med tall, finn maksimal lengde slangesekvens og skriv det ut. Hvis flere slangesekvenser eksisterer med maksimal lengde, skriv ut noen av dem.
En slangesekvens består av tilstøtende tall i rutenettet slik at for hvert tall tallet til høyre eller tallet under det er +1 eller -1 dets verdi. For eksempel hvis du er på stedet (x y) i rutenettet, kan du enten bevege deg til høyre, dvs. (x y+1) hvis antallet er ± 1 eller bevege deg ned, dvs. (x+1 y) hvis dette tallet er ± 1.
For example 9 6 5 2 8 7 6 5 7 3 1 6 1 1 1 7 In above grid the longest snake sequence is: (9 8 7 6 5 6 7)
Under figur viser alle mulige stier:

Vi anbefaler deg på det sterkeste å minimere nettleseren din og prøve dette selv først.
Tanken er å bruke dynamisk programmering. For hver celle i matrisen holder vi maksimal lengde på en slange som ender i nåværende celle. Maksimal lengde slangesekvens vil ha maksimal verdi. Den maksimale verdicellen vil samsvare med slangens haler. For å trykke slangen må vi spore tilbake fra hale helt tilbake til Snakes hode.
Let T[i][i] represent maximum length of a snake which ends at cell (i j) then for given matrix M the DP relation is defined as T[0][0] = 0 T[i][j] = max(T[i][j] T[i][j - 1] + 1) if M[i][j] = M[i][j - 1] ± 1 T[i][j] = max(T[i][j] T[i - 1][j] + 1) if M[i][j] = M[i - 1][j] ± 1
Nedenfor er implementeringen av ideen
C++ // C++ program to find maximum length // Snake sequence and print it #include using namespace std ; #define M 4 #define N 4 struct Point { int x y ; }; // Function to find maximum length Snake sequence path // (i j) corresponds to tail of the snake list < Point > findPath ( int grid [ M ][ N ] int mat [ M ][ N ] int i int j ) { list < Point > path ; Point pt = { i j }; path . push_front ( pt ); while ( grid [ i ][ j ] != 0 ) { if ( i > 0 && grid [ i ][ j ] - 1 == grid [ i - 1 ][ j ]) { pt = { i - 1 j }; path . push_front ( pt ); i -- ; } else if ( j > 0 && grid [ i ][ j ] - 1 == grid [ i ][ j - 1 ]) { pt = { i j - 1 }; path . push_front ( pt ); j -- ; } } return path ; } // Function to find maximum length Snake sequence void findSnakeSequence ( int mat [ M ][ N ]) { // table to store results of subproblems int lookup [ M ][ N ]; // initialize by 0 memset ( lookup 0 sizeof lookup ); // stores maximum length of Snake sequence int max_len = 0 ; // store coordinates to snake's tail int max_row = 0 ; int max_col = 0 ; // fill the table in bottom-up fashion for ( int i = 0 ; i < M ; i ++ ) { for ( int j = 0 ; j < N ; j ++ ) { // do except for (0 0) cell if ( i || j ) { // look above if ( i > 0 && abs ( mat [ i - 1 ][ j ] - mat [ i ][ j ]) == 1 ) { lookup [ i ][ j ] = max ( lookup [ i ][ j ] lookup [ i - 1 ][ j ] + 1 ); if ( max_len < lookup [ i ][ j ]) { max_len = lookup [ i ][ j ]; max_row = i max_col = j ; } } // look left if ( j > 0 && abs ( mat [ i ][ j - 1 ] - mat [ i ][ j ]) == 1 ) { lookup [ i ][ j ] = max ( lookup [ i ][ j ] lookup [ i ][ j - 1 ] + 1 ); if ( max_len < lookup [ i ][ j ]) { max_len = lookup [ i ][ j ]; max_row = i max_col = j ; } } } } } cout < < 'Maximum length of Snake sequence is: ' < < max_len < < endl ; // find maximum length Snake sequence path list < Point > path = findPath ( lookup mat max_row max_col ); cout < < 'Snake sequence is:' ; for ( auto it = path . begin (); it != path . end (); it ++ ) cout < < endl < < mat [ it -> x ][ it -> y ] < < ' (' < < it -> x < < ' ' < < it -> y < < ')' ; } // Driver code int main () { int mat [ M ][ N ] = { { 9 6 5 2 } { 8 7 6 5 } { 7 3 1 6 } { 1 1 1 7 } }; findSnakeSequence ( mat ); return 0 ; }
Java // Java program to find maximum length // Snake sequence and print it import java.util.* ; class GFG { static int M = 4 ; static int N = 4 ; static class Point { int x y ; public Point ( int x int y ) { this . x = x ; this . y = y ; } }; // Function to find maximum length Snake sequence path // (i j) corresponds to tail of the snake static List < Point > findPath ( int grid [][] int mat [][] int i int j ) { List < Point > path = new LinkedList <> (); Point pt = new Point ( i j ); path . add ( 0 pt ); while ( grid [ i ][ j ] != 0 ) { if ( i > 0 && grid [ i ][ j ] - 1 == grid [ i - 1 ][ j ] ) { pt = new Point ( i - 1 j ); path . add ( 0 pt ); i -- ; } else if ( j > 0 && grid [ i ][ j ] - 1 == grid [ i ][ j - 1 ] ) { pt = new Point ( i j - 1 ); path . add ( 0 pt ); j -- ; } } return path ; } // Function to find maximum length Snake sequence static void findSnakeSequence ( int mat [][] ) { // table to store results of subproblems int [][] lookup = new int [ M ][ N ] ; // initialize by 0 // stores maximum length of Snake sequence int max_len = 0 ; // store coordinates to snake's tail int max_row = 0 ; int max_col = 0 ; // fill the table in bottom-up fashion for ( int i = 0 ; i < M ; i ++ ) { for ( int j = 0 ; j < N ; j ++ ) { // do except for (0 0) cell if ( i != 0 || j != 0 ) { // look above if ( i > 0 && Math . abs ( mat [ i - 1 ][ j ] - mat [ i ][ j ] ) == 1 ) { lookup [ i ][ j ] = Math . max ( lookup [ i ][ j ] lookup [ i - 1 ][ j ] + 1 ); if ( max_len < lookup [ i ][ j ] ) { max_len = lookup [ i ][ j ] ; max_row = i ; max_col = j ; } } // look left if ( j > 0 && Math . abs ( mat [ i ][ j - 1 ] - mat [ i ][ j ] ) == 1 ) { lookup [ i ][ j ] = Math . max ( lookup [ i ][ j ] lookup [ i ][ j - 1 ] + 1 ); if ( max_len < lookup [ i ][ j ] ) { max_len = lookup [ i ][ j ] ; max_row = i ; max_col = j ; } } } } } System . out . print ( 'Maximum length of Snake ' + 'sequence is: ' + max_len + 'n' ); // find maximum length Snake sequence path List < Point > path = findPath ( lookup mat max_row max_col ); System . out . print ( 'Snake sequence is:' ); for ( Point it : path ) System . out . print ( 'n' + mat [ it . x ][ it . y ] + ' (' + it . x + ' ' + it . y + ')' ); } // Driver code public static void main ( String [] args ) { int mat [][] = {{ 9 6 5 2 } { 8 7 6 5 } { 7 3 1 6 } { 1 1 1 7 }}; findSnakeSequence ( mat ); } } // This code is contributed by 29AjayKumar
C# // C# program to find maximum length // Snake sequence and print it using System ; using System.Collections.Generic ; class GFG { static int M = 4 ; static int N = 4 ; public class Point { public int x y ; public Point ( int x int y ) { this . x = x ; this . y = y ; } }; // Function to find maximum length Snake sequence path // (i j) corresponds to tail of the snake static List < Point > findPath ( int [ ] grid int [ ] mat int i int j ) { List < Point > path = new List < Point > (); Point pt = new Point ( i j ); path . Insert ( 0 pt ); while ( grid [ i j ] != 0 ) { if ( i > 0 && grid [ i j ] - 1 == grid [ i - 1 j ]) { pt = new Point ( i - 1 j ); path . Insert ( 0 pt ); i -- ; } else if ( j > 0 && grid [ i j ] - 1 == grid [ i j - 1 ]) { pt = new Point ( i j - 1 ); path . Insert ( 0 pt ); j -- ; } } return path ; } // Function to find maximum length Snake sequence static void findSnakeSequence ( int [ ] mat ) { // table to store results of subproblems int [ ] lookup = new int [ M N ]; // initialize by 0 // stores maximum length of Snake sequence int max_len = 0 ; // store coordinates to snake's tail int max_row = 0 ; int max_col = 0 ; // fill the table in bottom-up fashion for ( int i = 0 ; i < M ; i ++ ) { for ( int j = 0 ; j < N ; j ++ ) { // do except for (0 0) cell if ( i != 0 || j != 0 ) { // look above if ( i > 0 && Math . Abs ( mat [ i - 1 j ] - mat [ i j ]) == 1 ) { lookup [ i j ] = Math . Max ( lookup [ i j ] lookup [ i - 1 j ] + 1 ); if ( max_len < lookup [ i j ]) { max_len = lookup [ i j ]; max_row = i ; max_col = j ; } } // look left if ( j > 0 && Math . Abs ( mat [ i j - 1 ] - mat [ i j ]) == 1 ) { lookup [ i j ] = Math . Max ( lookup [ i j ] lookup [ i j - 1 ] + 1 ); if ( max_len < lookup [ i j ]) { max_len = lookup [ i j ]; max_row = i ; max_col = j ; } } } } } Console . Write ( 'Maximum length of Snake ' + 'sequence is: ' + max_len + 'n' ); // find maximum length Snake sequence path List < Point > path = findPath ( lookup mat max_row max_col ); Console . Write ( 'Snake sequence is:' ); foreach ( Point it in path ) Console . Write ( 'n' + mat [ it . x it . y ] + ' (' + it . x + ' ' + it . y + ')' ); } // Driver code public static void Main ( String [] args ) { int [ ] mat = { { 9 6 5 2 } { 8 7 6 5 } { 7 3 1 6 } { 1 1 1 7 } }; findSnakeSequence ( mat ); } } // This code is contributed by Princi Singh
Python3 def snakesequence ( S m n ): sequence = {} DP = [[ 1 for x in range ( m + 1 )] for x in range ( n + 1 )] a b maximum = 0 0 0 position = [ 0 0 ] for i in range ( 0 n + 1 ): for j in range ( 0 m + 1 ): a b = 0 0 p = 'initial' if ( i > 0 and abs ( S [ i ][ j ] - S [ i - 1 ][ j ]) == 1 ): a = DP [ i - 1 ][ j ] if ( j > 0 and abs ( S [ i ][ j ] - S [ i ][ j - 1 ]) == 1 ): b = DP [ i ][ j - 1 ] if a != 0 and a >= b : p = str ( i - 1 ) + ' ' + str ( j ) elif b != 0 : p = str ( i ) + ' ' + str ( j - 1 ) q = str ( i ) + ' ' + str ( j ) sequence [ q ] = p DP [ i ][ j ] = DP [ i ][ j ] + max ( a b ) if DP [ i ][ j ] >= maximum : maximum = DP [ i ][ j ] position [ 0 ] = i position [ 1 ] = j snakeValues = [] snakePositions = [] snakeValues . append ( S [ position [ 0 ]][ position [ 1 ]]) check = 'found' str_next = str ( position [ 0 ]) + ' ' + str ( position [ 1 ]) findingIndices = sequence [ str_next ] . split () while ( check == 'found' ): if sequence [ str_next ] == 'initial' : snakePositions . insert ( 0 str_next ) check = 'end' continue findingIndices = sequence [ str_next ] . split () g = int ( findingIndices [ 0 ]) h = int ( findingIndices [ 1 ]) snakeValues . insert ( 0 S [ g ][ h ]) snake_position = str ( g ) + ' ' + str ( h ) snakePositions . insert ( 0 str_next ) str_next = sequence [ str_next ] return [ snakeValues snakePositions ] S = [[ 9 6 5 2 ] [ 8 7 6 5 ] [ 7 3 1 6 ] [ 1 1 10 7 ]] m = 3 n = 3 seq = snakesequence ( S m n ) for i in range ( len ( seq [ 0 ])): print ( seq [ 0 ][ i ] '' seq [ 1 ][ i ] . split ())
JavaScript function snakesequence ( S m n ) { let sequence = {} let DP = new Array ( n + 1 ) for ( var i = 0 ; i <= n ; i ++ ) DP [ i ] = new Array ( m + 1 ). fill ( 1 ) let a = 0 b = 0 maximum = 0 let position = [ 0 0 ] for ( var i = 0 ; i <= n ; i ++ ) { for ( var j = 0 ; j <= m ; j ++ ) { a = 0 b = 0 let p = 'initial' if ( i > 0 && Math . abs ( S [ i ][ j ] - S [ i - 1 ][ j ]) == 1 ) a = DP [ i - 1 ][ j ] if ( j > 0 && Math . abs ( S [ i ][ j ] - S [ i ][ j - 1 ]) == 1 ) b = DP [ i ][ j - 1 ] if ( a != 0 && a >= b ) p = String ( i - 1 ) + ' ' + String ( j ) else if ( b != 0 ) p = String ( i ) + ' ' + String ( j - 1 ) let q = String ( i ) + ' ' + String ( j ) sequence [ q ] = p DP [ i ][ j ] = DP [ i ][ j ] + Math . max ( a b ) if ( DP [ i ][ j ] >= maximum ) { maximum = DP [ i ][ j ] position [ 0 ] = i position [ 1 ] = j } } } let snakeValues = [] let snakePositions = [] snakeValues . push ( S [ position [ 0 ]][ position [ 1 ]]) let check = 'found' let String_next = String ( position [ 0 ]) + ' ' + String ( position [ 1 ]) let findingIndices = sequence [ String_next ]. split ( ' ' ) while ( check == 'found' ) { if ( sequence [ String_next ] == 'initial' ) { snakePositions . unshift ( String_next ) check = 'end' continue } findingIndices = sequence [ String_next ]. split ( ' ' ) let g = parseInt ( findingIndices [ 0 ]) let h = parseInt ( findingIndices [ 1 ]) snakeValues . unshift ( S [ g ][ h ]) let snake_position = String ( g ) + ' ' + String ( h ) snakePositions . unshift ( String_next ) String_next = sequence [ String_next ] } return [ snakeValues snakePositions ] } // Driver Code let S = [[ 9 6 5 2 ] [ 8 7 6 5 ] [ 7 3 1 6 ] [ 1 1 10 7 ]] let m = 3 let n = 3 let seq = snakesequence ( S m n ) for ( var i = 0 ; i < seq [ 0 ]. length ; i ++ ) console . log ( seq [ 0 ][ i ] + '' seq [ 1 ][ i ]. split ( ' ' ))
Produksjon
Maximum length of Snake sequence is: 6 Snake sequence is: 9 (0 0) 8 (1 0) 7 (1 1) 6 (1 2) 5 (1 3) 6 (2 3) 7 (3 3)
Tidskompleksitet av løsningen ovenfor er O (M*n). Hjelpeplass brukt av oppløsningen er O (M*n). Hvis vi ikke er pålagt å skrive ut slangeområdet, kan det reduseres ytterligere til O (n), da vi bare bruker resultatet fra siste rad.










![Hund lenket foran huset i Texas flomvann opp til hodet hennes [REDNINGSVIDEO]](https://techcodeview.com/img/trending/65/dog-chained-to-front-of-house-in-texas-flood-waters-up-to-her-head-rescue-video.webp)


