Et binært tre er balansert hvis høyden på treet er O(Log n) hvor n er antall noder. For eksempel opprettholder AVL-treet O(Log n)-høyden ved å sørge for at forskjellen mellom høydene til venstre og høyre undertrær er maksimalt 1. Rød-svarte trær opprettholder O(Log n)-høyden ved å sørge for at tallet av svarte noder på hver rot-til-blad-bane er den samme, og at det ikke er noen tilstøtende røde noder. Balanserte binære søk-trær er ytelsesmessig gode da de gir O(log n)-tid for søk, innsetting og sletting.

Et balansert binært tre er et binært tre som følger de 3 betingelsene:

• Høyden på venstre og høyre tre for noen node avviker ikke med mer enn 1.
• Det venstre undertreet til den noden er også balansert.
• Det høyre undertreet til den noden er også balansert.

En enkelt node er alltid balansert. Det er også referert til som et høydebalansert binært tre.

Eksempel :

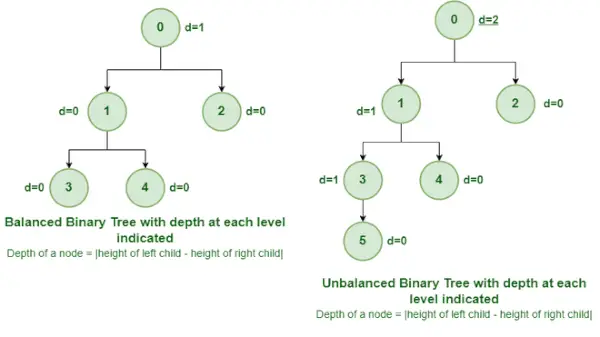
Balansert og ubalansert binært tre

Det er en type binært tre der forskjellen mellom høyden på venstre og høyre deltre for hver node er enten 0 eller 1. I figuren ovenfor er rotnoden med verdi 0 ubalansert med en dybde på 2 enheter .

Bruk av balansert binært tre:

• AVL trær
• Rødt svart tre
• Balansert binært søketre

Fordeler med balansert binært tre:

• Ikke-destruktive oppdateringer støttes av et balansert binært tre med samme asymptotiske effektivitet.
• Områdespørringer og iterasjon i riktig rekkefølge gjøres mulig av det balanserte binære treet.